ĆWICZENIE 31

BADANIE TRANSFORMATORA TRÓJFAZOWEGO

• Program ćwiczenia

• Pomiar rezystancji uzwojeń.

• Pomiar przekładni.

• Pomiar charakterystyk stanu jałowego.

• Pomiar charakterystyk zwarcia.

• Wyznaczenie zmienności napięcia.

• Wyznaczenie sprawności transformatora metodą strat poszczególnych.

• Cel ćwiczenia

Celem ćwiczenia jest poznanie ważniejszych prób i pomiarów wykonywanych podczas technicznego odbioru transformatora. Próby stanu jałowego, zwarcia i obciążenia dostarczają informacji pozwalających na ocenę jakości konstrukcji transformatora. Charakterystyki uzyskiwane w tych próbach ułatwiają zrozumienie zasady działania transformatora i zjawisk zachodzących w różnych stanach pracy.

• Omówienie programu ćwiczenia

Uzwojenie transformatora, które jest zasilane nazywa się uzwojeniem pierwotnym. Drugie z uzwojeń to uzwojenie wtórne. Te same uzwojenia w zależności od swych napięć znamionowych nazywają się uzwojeniem górnego lub uzwojeniem dolnego napięcia.

1. Pomiar rezystancji uzwojeń

Pomiar rezystancji uzwojeń należy wykonać metodą techniczną. Jeśli uzwojenia są połączone w gwiazdę lub zygzak z wyprowadzonym punktem zerowym, mierzy się rezystancje fazowe między odpowiednim zaciskiem a punktem zerowym. W przypadku połączenia uzwojeń w gwiazdę z izolowanym punktem zerowym mierzy się rezystancje między kolejnymi zaciskami faz R_AB, R_BC, R_CA, i następnie oblicza rezystancje fazowe ze wzorów

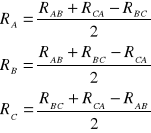
(31.1)

Dla uzwojeń połączonych w trójkąt mierzy się, jak poprzednio, rezystancje R_AB, R_BC, R_CA i oblicza rezystancje fazowe ze wzorów

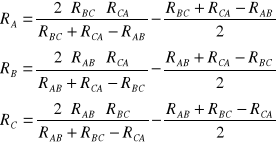
(31.2)

Zmierzone wielkości rezystancji należy przeliczyć na umowną temperaturę (348K dla izolacji klasy A, E, B lub 388K dla izolacji klasy F i H).

Rezystancję uzwojenia miedzianego przelicza się według wzoru

(31.3)

w którym: R^* -  rezystancja w umownej temperaturze pracy,

R -  rezystancja w temperaturze otoczenia,

T -  umowna temperatura pracy,

T_o -  temperatura otoczenia.

Dla każdego z uzwojeń należy wykonać po trzy pomiary, następnie obliczyć wartość średnią. Rezystancje fazowe transformatora nie powinny się różnić. Różnice większe niż 3% wartości średniej wymagają ustalenia ich źródła i stwierdzenia, czy nie dyskwalifikują one transformatora.

2. Pomiar przekładni

Przekładnią transformatora jest stosunek napięć znamionowych, występujących jednocześnie na zaciskach transformatora w stanie jałowym. Przekładnie transformatorów przeznaczonych do współpracy nie mogą się różnić więcej niż ± 0,5%. Z tego względu metoda pomiaru musi gwarantować dużą dokładność.

Przekładnie mierzy się jedną z dwóch metod:

1. kompensacyjną z zastosowaniem kompensatora Kellera,

2. woltomierzową, polegającą na jednoczesnym pomiarze napięć po obu stronach transformatora w stanie jałowym.

Rys. 31.1. Układ do pomiaru przekładni

Metodę woltomierzową stosuje się częściej, ponieważ jest prosta. Aby uzyskać wymaganą dokładność pomiaru, należy stosować woltomierz klasy 0,2. Pomiary wykonuje się w układzie przedstawionym na rysunku 31.1. Badany transformator zasila się obniżonym napięciem od strony górnego napięcia. Wskazania woltomierzy, przyłączonych do uzwojeń umieszczonych na tych samych kolumnach, powinny być odczytane jednocześnie. W ten sposób unika się błędów spowodowanych ewentualną asymetrią napięcia zasilania i jego wahaniami. Zmierzone wartości napięć należy zestawić w tabeli 31.1.

Tabela 31.1

Lp.

UAB

UBC

UCA

Uab

Ubc

Uca

ϑa

ϑb

ϑc

ϑśr

Uwagi

V

V

V

V

V

V

-

-

-

-

Na podstawie zmierzonych wartości napięć oblicza się przekładnię ze wzoru

(31.4)

przy czym: U_g0 - napięcie górne (U_AB, U_BC, U_CA),

U_d0 - napięcie dolne (U_ab, U_bc, U_ca).

Pomiar przekładni można też przeprowadzić zasilając transformator jednofazowo. Jeśli nie ma dostępnego punktu zerowego, mierzy się napięcia międzyfazowe.

Przekładnie ϑ_a, ϑ_b, ϑ_c, powinny być jednakowe i równe przekładni znamionowej ϑ_n, z uwzględnieniem odchyłek spowodowanych uchybami przyrządów i odczytów oraz tolerancji przekładni. W niektórych przypadkach może również być istotny uchyb spowodowany prądem woltomierza i prądem stanu jałowego transformatora.

1. Pomiar charakterystyk stanu jałowego

Charakterystyki strat jałowych, prądu stanu jałowego oraz współczynnika mocy w stanie jałowym informują o własnościach obwodu magnetycznego transformatora. Orientacyjny przebieg tych charakterystyk przedstawiono na rys. 31.2.

Wartość prądu jałowego, wyrażona w procentach prądu znamionowego i mierzona przy znamionowym napięciu, jest wielkością charakteryzującą transformator. Dla jednostek małych osiąga 10%, a dla jednostek największych mocy 1%.

Prąd jałowy można rozłożyć na składową czynną I_0w i składową bierną I_0μ. Składowa czynna jest w przybliżeniu proporcjonalna do napięcia U i odpowiada stratom mocy w rdzeniu transformatora. Przebieg charakterystyki składowej biernej I_0μ. = f(U₀) kształtem odpowiada charakterystyce magnesowania rdzenia. Wartości składowych prądu jałowego zależą od wartości współczynnika mocy:

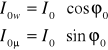
(31.5)

Wobec małej wartości współczynnika mocy (rys. 31.2) w całym zakresie napięć, składowa czynna prądu jałowego jest bardzo mała. Składowa bierna I_0μ. ma wartość zbliżoną do I₀. Można więc uważać, że charakterystyka I₀ = f(U₀) również odzwierciedla kształt krzywej magnesowania rdzenia. W prawidłowo skonstruowanym transformatorze punkt pracy przy znamionowym napięciu znajduje się na zakrzywieniu charakterystyki magnesowania. Gdy napięcie znamionowe badanego transformatora nie jest znane, można je w przybliżeniu określić na podstawie charakterystyki I₀ = f(U₀).

Moc pobrana przez transformator w stanie jałowym P₀ jest zużywana na pokrycie strat w rdzeniu ΔP_Fe, strat na rezystancji uzwojenia zasilanego 3·I₀²·R₁ oraz strat dielektrycznych w izolacji ΔP_iz

(31.6)

Straty w izolacji są niewielkie i zazwyczaj można je pomijać. Również straty w uzwojeniu są małe (szczególnie dla jednostek o małym prądzie jałowym) i w badaniach orientacyjnych można uważać, że P₀ = ΔP_Fe.

Straty w rdzeniu ΔP_Fe przy stałej częstotliwości zależą od masy żelaza m_Fe oraz indukcji B w potędze β zależnej od gatunku blach i wartości indukcji

(31.7)

W zakresie indukcji stosowanych w transformatorach β zawiera się w przedziale 2…3, przy czym wartości zbliżone do 2 odnoszą się do blach walcowanych na gorąco, a zbliżone do 3 odnoszą się do blach walcowanych na zimno. Przy stałej częstotliwości napięcie jest proporcjonalne do indukcji, więc straty w żelazie są proporcjonalne do U^β. Stąd wynika paraboliczny przebieg krzywej strat mocy na rys. 31.2.

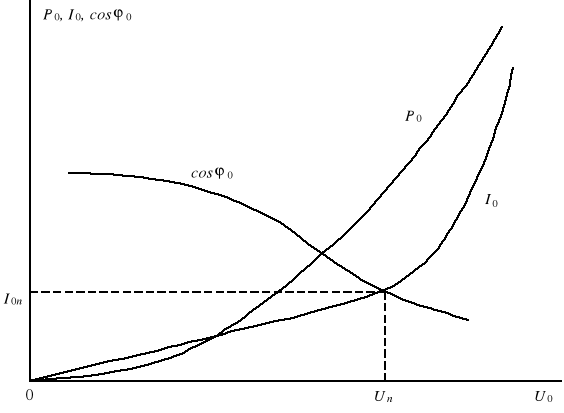
Rys. 31.2. Charakterystyki stanu jałowego

Pomiary charakterystyk stanu jałowego wykonuje się w układzie przedstawionym na rysunku 31.3. Ze względu na dokładność pomiarów oraz bezpieczeństwo obsługi pomiary przeprowadza się przy zasilaniu strony dolnego napięcia. Po stronie górnego napięcia pojawia się wówczas duża wartość napięcia, należy więc zachować szczególną ostrożność. Zmieniając napięcie od 0 do 1,1·U_n, mierzy się moc, prądy i napięcia, a wyniki notuje w tabeli 31.2.

Na podstawie wyników pomiarów należy obliczyć wartość współczynnika mocy

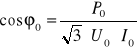
(31.8)

oraz strat w rdzeniu

(31.9)

a następnie sporządzić charakterystyki I₀, I_0w, P₀, cosϕ₀ = f(U₀).

Rys. 31.3. Układ do pomiaru charakterystyk stanu jałowego

Tabela 31.2

Lp.

Uab

Ubc

Uca

U0śr

Ia

Ib

Ic

I0śr

PI

PII

P0

ΔPFe

cosϕ0

I0w

I0μ

Uwagi

V

V

V

V

A

A

A

A

W

W

W

W

-

A

A

2. Pomiar charakterystyk stanu zwarcia

Zwarciem transformatora nazywa się stan, w którym jedno z uzwojeń zasilane jest obniżonym napięciem, podczas gdy zaciski drugiego uzwojenia są zwarte.

Celem próby zwarcia jest wyznaczenie napięcia zwarcia i strat obciążeniowych. Napięcie zwarcia jest to takie napięcie uzwojenia pierwotnego przy zwartym uzwojeniu wtórnym, pod wpływem którego w uzwojeniach transformatora płyną prądy znamionowe. Przy obniżonym napięciu, nie przekraczającym w czasie próby zwarcia kilkunastu procent wartości napięcia znamionowego, strumień magnetyczny w rdzeniu jest niewielki. Straty w rdzeniu są więc również małe i można uważać, że moc pobierana przez transformator równa jest stratom obciążeniowym. Próbę zwarcia wykonuje się w układzie przedstawionym na rys. 31.4.

Uzwojenie górnego napięcia zasila się napięciem regulowanym, a uzwojenie dolnego napięcia - zwiera. Zasilanie uzwojenia górnego napięcia jest podyktowane dokładnością pomiarów i łatwiejszym doborem przyrządów (wyższe napięcie i niższy prąd). Pomiary rozpoczyna się od takiej wartości napięcia, przy której prąd osiągnie wartość około 1.1·I_n. Następnie obniżając napięcie, mierzy się napięcia, prądy i moc pobieraną przez transformator. Wyniki pomiarów należy zestawić w tabeli 31.3.

Rys. 31.4. Układ do pomiaru charakterystyk stanu zwarcia

Tabela 31.3

Lp.

UAB

UBC

UCA

IA

IB

IC

Uzśr

Izśr

PI

PII

Pz

cosϕz

Rz

Xz

Uwagi

V

V

V

A

A

A

V

A

W

W

W

-

Ω

Ω

Współczynnik mocy podczas zwarcia cosϕ_z oblicza się ze wzoru

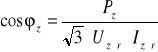
(31.10)

natomiast parametry schematu zastępczego, rezystancję R_z i reaktancję zwarcia X_z z zależności

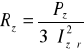
(31.11)

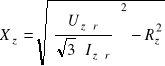
(31.12)

Na podstawie wyników pomiarów i obliczeń należy wykreślić charakterystyki I_z, P_z, cosϕ_z = f(U_z), których przykładowe przebiegi przedstawiono na rys. 31.5. Napięcie zwarcia odczytuje się z charakterystyki I_z = f(U_z) dla prądu znamionowego (I_z = I_n) i wyraża w procentach napięcia znamionowego (u_z). Wartość napięcia zwarcia powinna wynosić 3-12%, przy czym wartości większe odnoszą się do transformatorów dużej mocy.

3. Wyznaczenie zmienności napięcia

Zmianę napięcia strony wtórnej w zależności od zmian obciążenia, przy stałej wartości napięcia zasilania i stałym współczynniku mocy, ilustrują charakterystyki zewnętrzne U₂ = f(I₂). Przebiegi tych charakterystyk przy różnych rodzajach obciążenia pokazano na rysunku 31.6. Charakterystyki takie można uzyskać z próby obciążenia bezpośredniego lub wyznaczyć na podstawie wyników próby zwarcia. Względną zmianę napięcia strony wtórnej wywołaną zmianą obciążenia oblicza się ze wzoru:

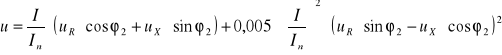
(31.13)

Rys. 31.5. Charakterystyki zwarcia

Względne wartości składowych czynnej i biernej napięcia zwarcia oblicza się z zależności

(31.14)

(31.15)

Można również obliczyć te składowe na podstawie odczytanych z wykresów P_z = f(U_z) i I_z = f(U) dla I = I_n strat mocy P_zn w uzwojeniach. Wówczas

(31.16)

(31.17)

Napięcie strony wtórnej oblicza się na podstawie względnej zmiany napięcia u ze wzoru

(31.18)

Aby wyznaczyć charakterystyki U₂ = f(I₂) dla stałego napięcia pierwotnego, stałej częstotliwości i stałego współczynnika mocy, należy obliczyć zmiany napięcia u oraz U₂ przyjmując różne wartości prądu obciążenia (np. I₂ = (0,25; 0,50; 0,75; 1,00; 1,25)·I_n) i współczynniki mocy cosϕ_2ind = 0,8 i cosϕ_2poj = 0,8. Wyniki obliczeń zestawić w tabeli 31.4.

Rys. 31.6. Charakterystyki zewnętrzne

Tabela 31.4

Lp.	I2/I2n	I2	u	U2	cosϕ2	sinϕ2	uR	uX	U2n	Uwagi
		-	A	-	V	-	-	-	-		V
	0,25 0,50 0,75 1,00 1,25				0,8	0,6				obciążenie indukcyjne
	0,25 0,50 0,75 1,00 1,25				0,8	-0,6				obciążenie pojemnościowe

Na podstawie wyników obliczeń należy wykreślić charakterystyki U₂ = f(I₂) dla cosϕ_ind = 0,8 i cosϕ_poj = 0,8 przy U₁ = U_n (rys. 31.6) oraz wyznaczyć zmienność napięcia transformatora. Zmienność napięcia jest to spadek napięcia na uzwojeniu wtórnym, występujący przy przejściu od stanu jałowego do obciążenia znamionowego przy stałym cosϕ₂, stałym napięciu pierwotnym i stałej częstotliwości, czyli

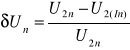
(31.19)

4. Wyznaczanie sprawności transformatora

Sprawność transformatora jest to stosunek mocy czynnej oddawanej do mocy czynnej pobieranej, a ta ostatnia jest sumą mocy oddawanej i całkowitych strat mocy

(31.20)

Straty całkowite ΔP_c są sumą strat obciążeniowych przeliczonych na umowną temperaturę pracy ΔP^*_obc oraz strat w rdzeniu ΔP_Fe

(31.21)

natomiast moc oddawana może być wyrażona przez znamionową moc pozorną S_n i wówczas

(31.22)

Straty w żelazie ΔP_Fe wyznacza się w próbie stanu jałowego dla napięcia znamionowego, natomiast straty obciążeniowe oblicza się ze wzorów

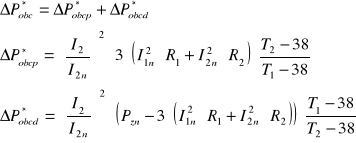
(31.23)

gdzie: ΔP^*_obcp - podstawowe straty mocy,

ΔP^*_obcd - dodatkowe straty mocy,

P_zn - moc pobrana w stanie zwarcia przy prądzie I_z = I_2n,

T₂ - umowna temperatura pracy [K],

T₁ - temperatura otoczenia, w której wyznaczono P_zn [K].

Obliczanie sprawności należy przeprowadzić dla dwóch wartości współczynnika mocy cosϕ₂ = 1 i cosϕ_2ind = 0,8, przyjmując prąd obciążenia I₂ = (0,25; 0,50; 0,75; 1,00; 1,25)·I_2n. Wyniki obliczeń zestawić w tabeli 31.5.

Tabela 31.5

Lp.	I2/I2n	I2	U	ΔPFe	ΔPzn	ΔP^*obc	ΔPc	P2	cosϕ2	η	Uwagi
	-	A	V	W	W	W	W	W	-	-
	0,25 0,50 0,75 1,00 1,25								1		obciążenie czynne
	0,25 0,50 0,75 1,00 1,25								0,8i		obciążenie indukcyjne

Na podstawie wyników obliczeń należy wykreślić charakterystyki η, ΔP_c = f(I₂) dla cosϕ₂ = 1 i cosϕ_2ind = 0,8 przy U₁ = U_n i f = f_n, których orientacyjne przebiegi podano na rysunku 31.7.

Należy również wyznaczyć znamionową sprawność transformatora tzn. sprawność przy znamionowym obciążeniu, współczynniku mocy cosϕ₂ = 1 i znamionowej temperaturze pracy uzwojeń.

Rys, 31.7. Charakterystyki robocze

• Sprawozdanie z ćwiczenia

Sprawozdanie z ćwiczenia powinno zawierać:

• protokół z pomiarów,

• wykresy charakterystyk stanu jałowego I₀, P₀, cosϕ₀ = f(U₀₁) przy f = f_n,

• wykresy charakterystyk stanu zwarcia I_z, P_z, cosϕ_z = f(U_z) przy U₂ = 0 i f = f_n,

• wykresy charakterystyk U₂ = f(I₂) przy cosϕ_2ind = 0,8 i cosϕ_2poj = 0,8 oraz U₁ = U_1n i f = f_n,

• obliczoną wartość zmienności napięcia δU,

• wykresy sprawności i strat całkowitych η, ΔP_c = f(I₂) dla cosϕ₂ = 1 i cosϕ_2ind = 0,8 przy U₁ = U_1n i f = f_n,

• obliczoną wartość sprawności znamionowej,

• uwagi i wnioski.

• Pytania kontrolne

• Co to jest przekładnia transformatora?

• W jaki sposób można określić orientacyjną wartość napięcia znamionowego transformatora?

• Z której strony należy zasilać transformator podczas prób stanu jałowego i zwarcia, i dlaczego?

• Uzasadnić przebieg składowej biernej prądu jałowego I_0μ w funkcji napięcia U₀.

• Co to jest napięcie zwarcia transformatora?

• Podać definicję zmienności napięcia.

• Omówić składniki strat mocy transformatora.

• Co to jest sprawność znamionowa?

107

---