1.Równania Maxwella

Równania Maxwella są podstawowymi równaniami elektromagnetyzmu. Wszystkie równania fizyki są w pewien sposób piękne. Mogą to ocenić ci, którzy je dobrze rozumieją. Takie są równania ruchu Newtona, zasady termodynamiki, teoria względności i teorie fizyki kwantowej.

Pierwsze z równań Maxwella to prawo Gaussa dla elektryczności. Dotyczy ładunku i pola elektrycznego. Prawo Gaussa zastosowane do dowolnej powierzchni podaje związek pomiędzy strumieniem pola elektrycznego Φ_E przechodzącym przez tę powierzchnię i całkowitym ładunkiem zamkniętym wewnątrz niej. Związek ten jest następujący

gdzie Φ_E oznacza strumień pola elektrycznego, ε_o to przenikalność dielektryczna próżni (8,85*10^-12 C²/Nm²), q to ładunek elektryczny, E jest natężeniem pola elektrycznego, zaś S to powierzchnia przez którą przechodzi strumień pola elektrycznego. Należy zauważyć, że q w równaniach jest ładunkiem wypadkowym, z uwzględnieniem znaku. Jeżeli powierzchnia zawiera ładunki równe co do wielkości bezwzględnej, ale o przeciwnych znakach, to strumień Φ_E jest równy zeru.

Prawo Gaussa może być użyte do wyznaczenia E, jeśli rozkład ładunków jest tak symetryczny, że przez odpowiedni wybór powierzchni Gaussa możemy łatwo obliczyć całkę w równaniu. Całka ta, zwana powierzchniową, oznacza, że rozpatrywaną powierzchnię, przez którą przenika strumień pola elektrycznego, należy podzielić na odpowiednią ilość elementów powierzchniowych dS, z jakiej się składa cała rozpatrywana powierzchnia. Kółko na znaku całki oznacz, że powierzchnia całkowania jest zamknięta.
Z prawa Gaussa można wyprowadzić prawo Coulomba. Wówczas ładunki jednoimienne odpychają się, a ładunki różnoimienne przyciągają się z siłą odwrotnie proporcjonalną do kwadratu odległości między nimi. Ładunek umieszczony na izolowanym przewodniku przemieszcza się w kierunku jego powierzchni zewnętrznej.

Drugie z równań Maxwella to prawo Gaussa dla magnetyzmu. Prawo Gaussa dla pola magnetycznego będące jednym z podstawowych równań elektromagnetyzmu jest formalnym stwierdzeniem wniosku wypływającego ze znanych faktów dotyczących elektromagnetyzmu, mianowicie wniosku o nieistnieniu izolowanych biegunów magnetycznych.

Prawo to stwierdza, że strumień pola magnetycznego Φ_B przechodzący przez dowolną zamkniętą powierzchnię gaussowską musi być równy zeru. Całka jest wzięta po całej zamkniętej powierzchni.

Trzecie równanie Maxwella dotyczy efektu elektrycznego zmieniającego się pola magnetycznego. Jest to tzw. prawo indukcji Faradaya. Prawo indukcji Faradaya głosi, że indukowana w obwodzie elektrycznym SEM równa jest szybkości, z jaką zmienia się strumień przechodzący przez ten obwód. Znak minus dotyczy kierunku indukowanej SEM, przeciwstawiającej się kierunkowi płynącego w obwodzie prądu elektrycznego.

Sztabka magnetyczna przesuwana przez zamknięty obwód powoduje powstanie prądu w tym obwodzie.

Ostatnie - czwarte równanie Maxwella związane jest z prawem Amper'a, które zostało rozszerzone przez Maxwella. Dotyczy ono efektu magnetycznego zmieniającego się pola elektrycznego.

Prąd płynący w przewodniku wytwarza wokół siebie pole magnetyczne. W równaniu μ_o oznacza przenikalność magnetyczną próżni, dl jest styczną do drogi całkowania, zaś i jest natężeniem płynącego prądu elektrycznego.

Zakres zastosowań równań Maxwella jest niezwykle duży, obejmuje on podstawowe zasady działania wszystkich makroskopowych urządzeń elektromagnetycznych, takich jak silniki, synchrotrony, telewizja, radar.

2. Fala elektromagnetyczna

Fala elektromagnetyczna to wzajemnie przenikające się drgania elektryczne i magnetyczne. Fala taka powstaje np. wtedy, gdy elektron w atomie traci energię i przeskakuje na orbitę bliżej jądra atomu. Powstają przy tym drgania elektryczne, które rozchodzą się w przestrzeni w postaci pola elektrycznego i magnetycznego. Pola te są prostopadłe do siebie i do kierunku rozchodzenia się fali. Pierwszym, który wprowadził pojęcie pola elektromagnetycznego był fizyk James Clerk Maxwell.

Cechą charakterystyczną fal elektromagnetycznych jest ich możliwość rozchodzenia się w próżni, czym w zasadniczy sposób różnią się od fal mechanicznych, które mogą się rozchodzić jedynie w ośrodkach sprężystych. Różni je także olbrzymia prędkość, z jaką się poruszają. Są to fale poprzeczne. Ich długość dana jest wzorem:

Podział fal elektromagnetycznych na poszczególne rodzaje dokonuje się ze względu na sposób ich wytwarzania. Fale radiowe czy mikrofale są wytwarzane sztucznie za pomocą przyrządów elektronicznych. Promieniowanie podczerwone, świetlne i ultrafioletowe powstaje wskutek zmian energetycznych, zachodzących w elektronowej powłoce wewnętrznej atomów lub cząsteczek. Promienie X powstają przez hamowanie w polu kulombowskim jąder sztucznie wytworzonej wiązki rozpędzonych elektronów lub wskutek przejść energetycznych, zachodzących w wewnętrznej powłoce elektronowej atomów. Promieniowanie gamma powstaje przy przejściach energetycznych wewnątrz wzbudzonych jąder. Promieniowanie kosmiczne powstaje podczas hamowania elektronów lub innych cząstek elementarnych o dużej energii w kulombowskim polu jąder atomowych.

3. Polaryzacja światła

Polaryzacja światła

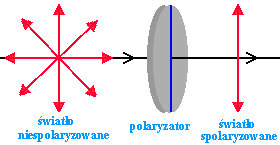
Światło to fala elektromagnetyczna, która polega na rozchodzeniu się zmian pola elektrycznego i magnetycznego. Wektory tych pól są prostopadłe do siebie i do kierunku rozchodzenia się. Jest to więc fala poprzeczna. Do określania ogientacji fali elektromagnetycznej bierzę się kierunek drgań pola elektrycznego. Nazywany jest on kierunkiem polaryzacji. Jeżeli drgania pola elektrycznego są w jednym kierunku to taką falę nazywamy spolaryzowaną liniowo (światło może być jeszcze spolaryzowane kołowo lub eliptycznie), jeśli drgania są w różnych kierunkach to niespolaryzowaną. Urządzenia służące do polaryzacji światła nazywamy polaryzatorami. Wykorzystują one jeden z trzech podstawowych sposobów polaryzacji światła.

Najpopularniejszymi polaryzatorami są używane przez fotografów polaroidy, specjalnie w tym celu wykonane płytki z polimerów. Pod dobrym mikroskopem można zobaczyć, że polaroid zbudowany jest z długich włókien tworzących szczeliny, przez które może przecisnąć się tylko światło o odpowiednim kierunku drgań. polaryzator przepuszcza tylko te fale, które mają kierunek drgań pola elektromagnetycznego zbliżony do kierunku wyznaczanego przez szczeliny polaryzatora, pozostałe fale są zatrzymywane.
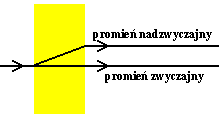
Naturalnymi polaryzatorami występującymi w przyrodzie są tak zwane kryształy dwójłomne, np. kalcyt (szpat islandzki), turmalin lub mika. Promień światła padający na taki kryształ

Przejście światła przy przejściu przez kryształy dwujłomne

ulega podwójnemu załamaniu i rozdziela się na dwa promienie, załamujące się pod różnymi kątami zwane promieniem zwyczajnym i nadzwyczajnym. Obydwa te promienie są spolaryzowane, ale w płaszczyznach do siebie prostopadłych. Własności kryształów dwujłomnych spowodowane są anizotropią, czyli mają różne właściwości w zależności od kierunku padania światła. W praktyce stosuje się układy pryzmatów wykonanych z materiałów dwujłonych, które albo rozdzielają wiązkę zwyczajna i nadzwyczjaną (pryzmaty polaryzujące dwuwiązkowe) lub wydzielają jeden ze spolaryzowanych promieni (pryzmaty jednowiązkowe).

Polaryzacja światła przez odbicie pod kątem Brewstera

W niektórych kryształach dwujłonych jeden z promieni (zwyczajny lub nadzwyczajny) jest silniej absorbowany w krysztale. Tkie kryształy zastosowano jako polaryzatory, na przykład turmalin o grubości 1 milimetr pochłąnia praktycznie w całości promień zwyczajny.
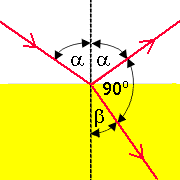
Światło ulega także polaryzacji (na ogół częściowej) przy odbiciu od powierzchni przezroczystych izolatorów, na przykład szkła lub wody. Całkowita polaryzacja światła odbitego zachodzi dla określonego kąta padania, zwanego kątem Brewstera. Jest to taki kąt padania, przy którym promień załamany tworzy z promieniem odbitym kąt 90°. Można wykazać, że tangens kąta Brewstera jest równy współczynnikowi załamania materiału substanci odbijającej. Dla szkła kąt ten wynosi około 55°. Przy całkowitej polaryzacji w świetle odbitym drgania pola elektrycznego odbywają się w płaszczyźnie prostopadłej do rysunku. Promień załamany jest również częściowo spolaryzowany, ale nigdy całkowicie.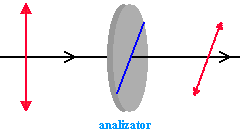

Polaryzatory liniowe przepuszczają światło o kierunku drgań pola elektrycznego tylko w jednym kierunku. Jeśli światło spolaryzowane pada na drugi polaryzator o innym kierunku

polaryzacji, to część energii niesiona przez falę zostaje pochłonięta w materiale tego polaryzatora, a fala przechodząca jest spolaryzowana zgodnie z jego kierunkiem polaryzacji. Drugi polaryzator może więc zmienić kierunek polaryzacji światła, które nań pada. Jeżeli płaszczyzny polaryzacji są takie same, to efekt jest taki jak dla jednego polaryzatora. Drugi polaryzator więc może odgrywać rolę analizatora. Obracając go, możemy sprawdzić, czy padające na niego światło było spolaryzowane i w jakiej płaszczyźnie (światło przechodzi lub zostaje pochłonięte). Jeżeli analizator zostanie ustawiony prostopadle do polaryzatora to światło dalej nie przejdzie. Ilość światła, które przechodzi przez analizator ustawiony pod dowolnym kątem do polaryzatora, podaje prawo Malusa, którego tutaj nie omawiamy.

Naturalne światło pochodzące ze Słońca, żarówki lub świetlówki nie jest spolaryzowane. Polazyzację otrzymujemy po odbiciu światła od szyby, tafli wody lub mokrej jezdni. Również światło rozproszone przez chmury jest częściowo spolaryzowane. Płaszczyzna liniowej polaryzacji światła rozproszonego przez atmosferę (niebo) jest prostopadła do kierunku, z którego świeci Słońce. Światło wysyłane przez laser jest całkowicie spolaryzowane, co widać podczas obrotu polaryzatora.
Spolaryzować można każdą falę poprzeczną, na przykład falę na sznurze. Fali podłużnej, czyli takiej dla której drgania są równoległe do kierunku rozchodzneia się spolaryzować się nie da. Nie można więc spolaryzować fali dźwiękowej w powietrzu bo jest to fala podłużna.

4. Prawo Malusa dotyczy zmiany natężenia światła przechodzącego prezez analizator, w zależnośći od kąta, jaki tworzą płaszczyzny transmisji analizatora i polaryzatora. Obserwując wiązkę spolaryzowaną liniowo w kierunku pionowym, patrząc wzdłuż kierunku jej rozchodzenia się w stronę, z której wiązka nadbiega. Oznaczmy przez A₁ amplitudę tego swiatła. Światło pada na analizator, którego płaszczyzna transmisji twoży z A₁ kąt θ. Żeby znaleźć amplitudę A₂ światła przechodzącego, znajdujemy składową amplitudy A₁ w ierunku wyznaczonym przez płaszczyznę transmisji analizatora. A₂=A₁cosθ Ponieważ natężenie światła jest równe kwadratowi amplitudy, wobec tego I₂=I₁cos²θ. Każda absorpcja w polaryzatorze wprowadzi do tego równania pewną stałą, ale nie zmieni to zależnośći względnego natężenie od cos²θ. Prawo Malusa jest spełniane ściśle.

Ćwierćfalówka i jej działanie
Płytka krystaliczna, która wytwarza pomiędzy promieniami zywczajnym i nadzwyczajnym przechodzącymi przez nią różnicę fazy λ/4 lub 3λ/4. Odpowiada to różnicy dróg jednej czwartej lub trzem czwartym długośći fali¹. Ćwierćfalówki najczęściej wykonane są z miki. Ćwierćfalówka daje różnicę fazy równą π/2 promieni o określonej długości fali; dla innych długości fal różnica fazy jest inna. Najczęściej ćwierćfalówki wykonane są tak, aby otrzymać różnicę fazy π/2 dla barwy odpowiadającej żółtej linii sodowej lub najśilniejszym liniom widma rtęci. Spośród dwóch kierunków drgań rozchodzących się z większą prędkością nazywamy pierwszym azymutem ćwierćfalówki, zaś kierunek drgania rozchodzącego się z prędkością mniejszą - drugim azymutem. Zazwyczaj ustawiamy ćwierćfalówkę w ten sposób, by pierwszy azymut leżał w płaszczyźnie pionowej. Jeżeli płaszczyzna polaryzacji światła padającego na ćwierćfalówkę jest równoległa do jednego z azymutów, to światło przechodzące jest nadal spolaryzowane liniowo. Gdy płaszczyzna polaryzacji światła padającego na ćwierćfalówkę tworzy pewien kąt α≠0 z azymutami, wtedy drganie światła rozkłada się na dwie składowe: zwyczajną i nadzwyczajną. Każda z nich rozchodzi się z inną prędkością i po przejściu przez płytkę powstaje różnica faz ±λ/4. Stąd też obydwie fale nakładając się dają w wyniku światło spolaryzowane wliptycznie. W szególnym przypadku, gdy płaszczyzna polaryzacji światła padającego tworzy z azymutami kąt α=π/4, otrzymujemy światło spolaryzowane kołowo.

5. Dwójłomność wymuszona

W ośrodkach anizotropowych prędkość światła zależy od kierunku. Efekt ten występuje w większości kryształów, które nazywamy dwójłomnymi. Wiązka światła, biegnąc w ośrodku dwójłomnym, rozdziela się na dwie wiązki spolaryzowane w kierunkach wzajemnie prostopadłych. Wiązki te poruszają się z różnymi prędkościami fazowymi. Związana z tymi prędkościami różnica współczynników załamania:

Zjawisko to może wystąpić w ciałach izotropowych pod wpływem czynników zewnętrznych: pola elektrycznego, magnetycznego lub przyłożonych sił.

Skręcenie płaszczyzny polaryzacji:

6,9,10. Interferencja

to zjawisko nakładania się fal prowadzące do zwiększania lub zmniejszania amplitudy fali wypadkowej. Interferencja zachodzi dla wszystkich rodzajów fal, we wszystkich ośrodkach, w których mogą rozchodzić się dane fale. W ośrodkach nieliniowych oprócz interferencji zachodzą też inne zjawiska wywołane nakładaniem się fal, w ośrodkach liniowych fale ulegając interferencji spełniają zasadę superpozycji.
W najprostszym przypadku, aby zaszła interferencja muszą być spełnione następujące warunki ₁=₂ oraz ₁(t)-₂(t)=const.

    Podczas nakładania się światła pochodzącego z dwóch źródeł nie będących laserami lub nawet pochodzących z różnych miejsc tego samego źródła nie obserwujemy interferencji. Jest to spowodowane przez emisję światła przez wzbudzone atomy w postaci skończonych ciągów falowych, których fazy początkowe zmieniają się niezależnie. Dwie fale nazywamy falami spójnymi jeżeli różnica ich faz nie zależy od czasu. Spójne fale świetlne ze zwykłych (nielaserowych) źródeł otrzymujemy metodą dzielenia światła pochodzącego z jednego źródła na dwie lub więcej wiązek. Promieniowanie w każdej z nich pochodzi od tych samych atomów źródła i ze względu na wspólne pochodzenie, wiązki te są spójne. Do podziału światła na wiązki spójne można wykorzystać zjawiska odbicia lub załamania światła.
Okazuje się jednak, że powyższe warunki są zbyt silne i interferencję możemy obserwować nawet wtedy, gdy częstości nakładających się fal nie są dokładnie równe. Również nie musimy używać źródeł o punktowych rozmiarach. W ogólności, interferujące ze sobą fale muszą mieć spełnione tzw. warunki spójności czasowej i przestrzennej.

prążki interferencyjne, fiz. na przemian ciemne i jasne, na ogół barwne (w przypadku światła niemonochromatycznego) pasma powstałe w wyniku interferencji wiązek światła przebywających różne drogi opt.

interferencja równej grubości i równego nachylenia
Przy interferencji światła zachodzącej dzięki wielokrotnemu odbiciu w płytce płasko-równoległej otrzymane prążki nazywa się prążkami (interferencyjnymi) równego nachylenia, przy interferencji otrzymywanej dzięki odbiciom w płytce o innych kształtach (klinowatej, sferycznej itp.) otrzymuje się tzw. prążki równej grubości.

7. Doświadczenie Younga - eksperyment polegający na przepuszczeniu spójnego światła poprzez dwa pobliskie otwory w przesłonie i rzutowaniu na ekran. Na ekranie wskutek interferencji tworzą się charakterystyczne prążki, tzn. obszary w których światło jest wygaszone i wzmocnione.

warunek powstania maksimum

warunek powstania minimum

gdzie: d jest odległością pomiędzy podwójnymi szczelinami, λ - długość fali a α - kąt pod jakim maksimum lub minimum obserwowane jest na ekranie.

Eksperyment ten potwierdził falową naturę światła i stanowił poważny argument przeciwko korpuskularnej koncepcji światła, której zwolennikiem był Isaac Newton. Po raz pierwszy eksperyment ten wykonał około roku 1805 Thomas Young, fizyk angielski.

Bardziej widowiskowy i łatwiejszy sposób wykonania tego doświadczenia, polega na użyciu siatki dyfrakcyjnej, czyli płytki ze szkła, na której gęsto zarysowane są rysy pełniące rolę przesłon pomiędzy szczelinami. Obraz interferencyjny widoczny w tym przypadku na ekranie jest znacznie wyraźniejszy i jaśniejszy niż przy użyciu jedynie dwóch szczelin.

Thomasa Younga zainspirowały obserwacje fal na wodzie pochodzących z dwóch różnych źródeł - ich wzajemne wzmacnianie się i osłabianie. Chcąc wykonać podobny eksperyment z użyciem światła, użył nieprzezroczystego materiału, w którym wyciął dwie bardzo małe dziurki. Do uzyskania spójnego światła Young przepuścił światło świecy najpierw przez pojedynczy mały otwór. Światło to, zgodnie z Zasadą Huygensa rozchodziło się w postaci fali kulistej a następnie docierało do dwóch szczelin na kolejnej przesłonie. Różnica faz promieni dochodzących do obu szczelin była cały czas jednakowa dla danej częstotliwości, a zatem były to fale spójne. Po przejściu przez obie szczeliny, promienie rozprzestrzeniały się (znów zgodnie z zasadą Huygensa) i oświetlały ekran tworząc na nim kolorowe prążki interferencyjne.

Doświadczenie w swojej pierwotnej formie nie budziło wielkich kontrowersji w świecie fizyki, jednak późniejsze jego modyfikacje postawiły przed fizykami znaki zapytania. Okazało się bowiem, że nawet pojedyncze fotony wysyłane przez szczeliny w znacznych odstępach czasu, które nie miały prawa wzajemnie ze sobą interferować, tworzyły za szczelinami na światłoczułym materiale wzór interferencyjny. Efekt ten będąc jedną z manifestacji kwantowej natury światła jest często używany do objaśniania podstaw mechaniki kwantowej.

W kwantowo-mechanicznym podejściu efekt interferencji spowodowany jest nakładaniem się funkcji falowej opisującej stan fotonu.

8. Koherencja (z łac. oznacza spójność, spoistość, łączność), w fizyce koherencja fal (spójność fal), oznacza zdolność fal (świetlnych, dźwiękowych itp.) do dawania trwałych efektów interferencyjnych. Fale są spójne (spójność fal) jeśli ich wiązki mają tę samą częstotliwość i stałą w czasie różnicę faz.

Innymi słowy spójność fal jest to własność np. dwóch fal, dzięki której ich nakładanie się czyli interferencja jest stabilne w czasie (np. obraz interferencyjny spójnych fal świetlnych można zaobserwować lub nawet sfotografować. Dwie fale są spójne tylko wtedy, gdy mają tę samą częstość i stałą różnicę faz.

Światło spójne (ś. koherentne)

1. (W znaczeniu szerszym) Światło zdolne do interferencji.

Mówimy, że dwa promienie są spójne, jeśli mają tę samą długość fali (ś. monochromatyczne), amplitudę, stałą w czasie różnicę faz oraz taką samą płaszczyznę polaryzacji, dzięki czemu w wyniku interferencji dają stałe obszary wzmocnienia i osłabienia w postaci prążków interferencyjnych, pierścieni i in.

2. (W znaczeniu węższym) Światło składające się z fotonów zgodnych w fazie.

Źródła światła takie jak: Słońce, płomień, żarówka wytwarzają światło niespójne. Nawet, jeżeli jest ono monochromatyczne i ma stałą amplitudę nie występuje zgodność fazowa. Jednak w małej skali czasowej

źródło emituje pojedynczy spójny ciąg falowy. Mówimy wówczas o spójności czasowej (ograniczonej w czasie). Ciąg ten poruszając się z prędkością światła jest w danej chwili czasu spójny na drodze (spójność przestrzenna)

Dzięki istnieniu spójnych ciągów falowych, można uzyskiwać efekty interferencyjne. Jeżeli na drodze światła umieścimy wąską szczeliną, wówczas w danym momencie czasu przejdzie przez nią jeden ciąg falowy. Rozprzestrzeniający się ciąg falowy można przepuścić z kolei przez dwie szczeliny uzyskując prążki interferencyjne Doświadczenie Younga. Podobnie można uzyskać efekt interferencyjny w cienkich warstwach, gdy światło odbite od górnej powierzchni warstwy nakłada się na światło odbite od dolnej powierzchni warstwy.

Światło o dużej spójności czasowej i przestrzennej uzyskać można dzięki laserom

12,13. Dyfrakcja Fraunhofera

Zasada Huyghensa; każdy punkt do którego dociera czoło fali staje się źródłem nowej fali elementarnej. Superpozycja wszystkich fal elementarnych daje nowe czoło fali

W oparciu o zasadę Huyghensa możemy znaleźć pole fali świetlnej w dowolnym punkcie na ekranie, całkując wkłady od oscylatorów Huyghensa rozmieszczonych na powierzchni otworu w nieprzeźroczystym ekranie znajdującym się pomiędzy źródłem fali pierwotnej i ekranem.

Dyfrakcja Fraunhofera na pojedynczym otworze prostokątnym prowadzi do powstania charakterystycznego „krzyża” odpowiadającego nałożeniu dwóch rozkładów opisanych funkcjami:

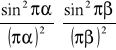
Obrazy dyfrakcyjne otworów o większej liczbie krawędzi pokazują rozdzielne zbiory liniowych prążków równoległych do każdej krawędzi. Krawędziom zakrzywionym towarzyszą prążki o pewnej krzywiźnie, rosnącej długości i szybko malejącym natężeniu w miarę oddalania się od centrum obrazu dyfrakcyjnego.

Dyfrakcja Fresnela i zasada Huygensa-Fresnela. 

Fresnel przy rozpatrywaniu dyfrakcji światła oparł się na kilku podstawowych prawach przyjętych bez dowodu i stanowiących treść tzw. Zasady Huygensa zgodnie z którą każdy element powierzchni falowej stanowi źródło kulistej fali wtórnej (rysunek poniżej).

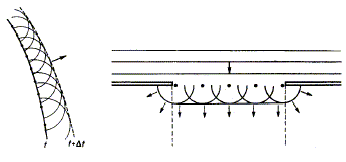
Zasada ta nie pozwala jednak uzyskać żadnych informacji o amplitudzie i natężeniu fal rozchodzących się w różnych kierunkach. Fresnel uzupełnił ją o pojęcie interferencji fal wtórnych. Uwzględnienie amplitud i faz tych fal pozwala obliczyć amplitudę fali wypadkowej w dowolnym punkcie przestrzeni (uzupełniona w ten sposób zasada otrzymała nazwę zasady Huygensa-Fresnela). Zrealizowanie powyższego zagadnienia w praktyce bywa jednak niezmiernie trudne. Tu jednak przychodzi nam z pomocą metoda stref Fresnela. Polega ona mianowicie na rozbiciu powierzchni falowej na strefy w taki sposób, by odległości od skrajów każdej strefy do punktu, w którym mierzymy natężenie różniły się o pół długości fali.
Na przykładzie fali kulistej widzimy jak można podzielić powierzchnie falową na strefy pierścieniowe, żeby drgania pochodzące od sąsiednich stref były w przeciwfazie. Teraz możemy zasłonić wszystkie strefy parzyste lub nieparzyste. Zaobserwujemy silny wzrost natężenia (ponieważ strefy znajdujące się w przeciwfazie osłabiają się wzajemnie).

Płytkę, która zakrywa wszystkie strefy jednego rodzaju nazywamy płytką strefową amplitudową (rysunek) - działa ona analogicznie do soczewki skupiającej. Jeszcze większego efektu można oczekiwać zmieniając fazy drgań jednego rodzaju stref o sto osiemdziesiąt stopni (za pomocą płytki strefowej fazowej).

Dyfrakcja Fresnela to dyfrakcja fal kulistych. Znacznie prościej jest jednak w wielu przypadkach rozwiązać problem dyfrakcji fal płaskich, dlatego czasem stosuje się przejście od dyfrakcji bliskiego pola (dyfrakcji Fresnela) do dyfrakcji dalekiego pola zwanej też dyfrakcją Fraunhofera. Można to zrobić, o ile punkt, w którym obserwujemy natężenie jest bardzo oddalony od otworu dyfrakcyjnego lub też fala kulista przychodzi z tak daleka (jej promień jest tak wielki), że możemy ją uznać za „lokalnie” płaską.

14. Zdolność rozdzielcza- Zdolność układu optycznego (w przypadku aparatu zestawu: obiektyw i detektor) do rozróżnienia na przykład określonej liczby linii na 1 milimetr obrazu przy optymalnych warunkach naświetlania i obróbki.

Za rozdzielczość optyki odpowiedzialna jest falowa natura światła, która jest przyczyną dyfrakcji, czyli odchylania się światła przy brzegu oprawy obiektywu. Efekt ten powoduje, że punktowe źródła, które chcemy uwiecznić na obrazie nie są już punkami lecz plamami nazywanymi przez optyków krążkami dyfrakcyjnymi otoczonymi dodatkowymi ciemnymi i jasnymi pierścieniami dyfrakcyjnymi. Rozmiar takiego krążka, a co za tym idzie teoretyczna zdolność rozdzielcza naszego instrumentu, zależy tylko od światłosiły obiektywu (zastosowanej wartości przesłony) i długości fali odbieranego światła. Zakładając dla uproszczenia, że mamy do czynienia z monochromatycznym światłem o długości 550 nanometrów otrzymujemy, iż teoretyczna odległość na matrycy pomiędzy dwoma punktami, którą jesteśmy w stanie odróżnić (wyrażona w mikrometrach) opisana jest wzorem 1.34*F. Oznacza to, że przy przesłonie 3.5 wynosi ona 4.7 mikrometra, a przy przesłonie 11 aż 14.8 mikrometra. Oczywiście to tylko teoria, bo wszelkiego rodzaju wady optyczne, winietowanie oraz straty światła w szkle i na powłokach antyodbiciowych dodatkowo rozmazują uzyskiwany obraz, psując rozdzielczość nawet kilkukrotnie. Dodatkowo, ze względu na wzrost wad optycznych i winietowania wraz z oddaleniem się od osi optycznej układu, rozdzielczość spada w trakcie przesuwania się do brzegu obrazu.

Stała siatki dyfrakcyjnej określa jej dyspersję kątową dϕ/dλ - tj. wielkość charakteryzującą zmianę kąta ugięcia ϕ promienia świetlnego na siatce wraz ze zmianą długości fali światła λ - która wyrażona jest równaniem:

gdzie m (tzw. rząd widma) jest liczbą naturalną określającą różnicę faz interferujących ze sobą promieni, podaną w okresach drgań tej fali.

Kryterium Rayleigha - orientacyjne kryterium pozwalające ocenić, czy dwie linie widmowe światła są rozdzielone. Lord Rayleigh, najprawdopodobniej autor pojęcia "zdolność rozdzielcza", za warunek rozróżnialności obrazów dyfrakcyjnych dwóch równoległych linii widmowych przyjął następujące kryterium:

Maksimum jednego obrazu dyfrakcyjnego leży w miejscu minimum drugiego obrazu^[1].

Kryterium to stosowane jest do określania zdolności rozdzielczej elementów i układów optycznych. Nie jest ono ścisłym prawem i ma charakter jedynie narzędzia pomocniczego. W zależności od warunków (natężenia światła, braku lub obecności światła rozproszonego, powierzchni ekranu) można rozróżniać obiekty, które nie spełniają ściśle kryterium Rayleigha. W niesprzyjających warunkach, nawet obrazy spełniające warunek Rayleigha mogą pozostać nierozróżnialne.

Kryterium Rayleigha, w powyższym słownym sformułowaniu, dotyczy rozdzielczości liniowej. Określa się je również dla rozdzielczości kątowej, ponieważ w rzeczywistych układach optycznych promienie tworzące nakładające się obrazy dyfrakcyjne nie są ściśle równoległe, chociaż kąt między nimi, w przypadku określania rozdzielczości, pozostaje bardzo mały. Dla obrazów dyfrakcyjnych powstałych po przejściu światła przez otwór kołowy warunek Rayleigha można zapisać wzorem

gdzie:

- minimalny kąt między promieniami, których obrazy mają być rozróżnialne, czyli inaczej - ich odległość kątowa;

λ - długość fali światła;

d - średnica otworu.

Ponieważ kąt φ jest bardzo mały, można zapisać w przybliżeniu:

Zdolność rozdzielcza przyrządów optycznych
W przypadku soczewki do określenia kątowej zdolności rozdzielczej stosuje się wzór (2), przy czym d oznacza tu średnicę soczewki. Liniowa zdolność rozdzielcza doskonałej soczewki o ogniskowej f wyraża się wzorem

przy czym l należy rozumieć jako minimalną odległość obiektów, które są jeszcze rozróżnialne. Wzory powyższe stosuje się również do obiektywów, lecz w tym przypadku d oznacza efektywną średnicę obiektywu, zależną od jego budowy i stosowanej przesłony. W przypadku teleskopu przyjmuje się trochę słabsze kryterium zdolności rozdzielczej.

15. Ciało doskonale czarne - ciało pochłaniające całkowicie padające na nie promieniowanie elektromagnetyczne, niezależnie od temperatury tego ciała, kąta padania i widma padającego promieniowania.

Plancka prawo promieniowania, prawo opisujące emisję światła przez ciało doskonale czarne znajdujące się w danej temperaturze.

Zgodnie z nim emisja (i absorpcja) światła odbywa się w porcjach (kwantach) o energii hν, gdzie h - stała Plancka, ν - częstotliwość fali światła, a zależność zdolności emisyjnej ε od częstotliwości fali ν i temperatury T wyrażona jest wzorem (tzw. wzór Plancka):

gdzie c - prędkość światła, k - stała Boltzmanna.

16. Fotoefekt

Efekt fotoelektryczny, zjawisko fotoelektryczne - zjawisko fizyczne polegające na emisji elektronów z powierzchni przedmiotu (tzw. efekt zewnętrzny) lub na przeniesieniu nośników ładunku elektrycznego pomiędzy pasmami energetycznymi (tzw. efekt wewnętrzny), po naświetleniu jej promieniowaniem elektromagnetycznym (na przykład światłem widzialnym) o odpowiedniej częstotliwości, zależnej od rodzaju przedmiotu. Emitowane w ten sposób elektrony nazywa się czasem fotoelektronami. Energia kinetyczna fotoelektronów nie zależy od natężenia światła a jedynie od jego częstotliwości. Gdy oświetlanym ośrodkiem jest gaz mamy do czynienia z tzw. fotojonizacją.

Odkrycie i wyjaśnienie efektu fotoelektrycznego przyczyniło się do rozwoju korpuskularno-falowej teorii materii, w której obiektom m

17. Promieniowanie rentgenowskie (w wielu krajach nazywane promieniowaniem X lub promieniami X) - to rodzaj promieniowania elektromagnetycznego, którego długość fali mieści się w zakresie od 10 pm do 10 nm. Zakres promieniowania rentgenowskiego znajduje się pomiędzy ultrafioletem i promieniowaniem gamma. Znanym skrótem nazwy jest promieniowanie rtg.
Właściwości promieni rentgenowskich
1.Rozchodzą się prostoliniowo
2.Są niewidzialne,ale wywołują fluorescencję
3.Wywołuje jonizację powietrza
4.Przenika przez szkło,czrny papier, a nawet przez płytki metalowe
5.Zaczernia kliszę fotograficzną
6.Są pochłaniane bardziej przez pierwiastki o większej liczbie porządkowej Z

Promieniowanie charakterystyczne to zwyczajowa nazwa linii widmowych atomów pierwiastków, powstających w wyniku wybicia elektronu z dolnych powłok elektronowych i przejścia elektronów "w dół". Związane jest to z tym, że gdy nastąpi wybicie elektronu z niskiej powłoki (np. K, lub L) następuje wzbudzenie atomu (atom bez elektronu z powłoki K ma większą energię niż z), które po pewnym czasie zanika w wyniku kaskadowego przejścia elektronów na niższe powłoki (efekt Augera). Dla pierwiastków ciężkich promieniowanie charakterystyczne jest promieniowaniem Rōntgena.

Promieniowanie hamowania, promieniowanie rentgenowskie lub gamma emitowane przez cząstkę naładowaną podczas jej wnikania do materii. Promieniowanie hamowania powstaje w wyniku oddziaływania cząstki z polami elektrostatycznymi jąder i elektronów w materii. Powstawanie promieniowania hamowania wykorzystuje się do uzyskiwania intensywnych wiązek promieniowania rentgenowskiego w lampach rentgenowskich.

Promieniowanie hamowania powstaje też jako uboczne promieniowanie w lampach kineskopowych (np. w telewizorze), lecz jego natężenie jest małe i równie mała jest jego szkodliwość.

18. Foton, kwant pola promieniowania elektromagnetycznego. Masa spoczynkowa fotonu równa jest zero (oszacowanie eksperymentalne daje wielkość < 10^-48g), porusza się z prędkością światła c, ma energię E=hν, (h - stała Plancka, ν - częstotliwość odpowiadającej fali elektromagnetycznej), jest bozonem, nie posiada momentu magnetycznego ani ładunku elektrycznego.

Fotony powstają w wyniku przejścia układu, np. atomu lub jądra atomowego ze stanu wzbudzonego do stanu o niższej energii, podczas zmiany pędu cząstki naładowanej, a także w wyniku anihilacji par elektron-pozyton.

Zjawisko Comptona polega na zmianie długości fali promieniowania rentgenowskiego podczas rozpraszania tego promieniowania przez substancję zawierającą lekkie atomy.

Promieniowanie rozproszone na elektronie pod kątem w stosunku do kierunku rozchodzenia się tego promieniowania zmienia długość (na większą) - zmiana długości równa jest

Rys. Natężenie wiązki rozproszonej pod kątem
w zależności od długości fali (
=
₁,
'=
₂).

19. Hipoteza de Broglie'a zakłada, że wszystkie cząstki takie jak protony, elektrony, neutrony można traktować jako fale.
Fale materii, zwane też falami de Broglie'a jest to, alternatywny w stosunku do klasycznego (czyli korpuskularnego), sposób postrzegania obiektów materialnych. Według hipotezy dualizmu korpuskularno-falowego każdy obiekt może być opisywany na dwa sposoby: jako cząstka/obiekt materialny albo jako fala (materii).

Fale de Broglie, fale materii, jeden z aspektów istnienia materii. Cząstki elementarne i inne obiekty mikroświata w pewnych warunkach wykazują właściwości typowe dla fal (np. ulegają zjawisku dyfrakcji). Każdej cząstce swobodnej o pędzie p można przypisać długość fali λ = h/p,

Pomysł opisu cząstek za pomocą fal pochodzi od Louisa de Broglie'a, który w 1924 roku uogólnił teorię fotonową efektu fotoelektrycznego. W tym czasie wiedziano już, że na potrzeby opisu niektórych zjawisk fizycznych, z każdą falą elektromagnetyczną można stowarzyszyć pewną cząstkę - foton.

Podobnie każdej cząstce o energii E należy przyporządkować inną typową charakterystykę fali, tj. częstotliwość. Wynosi ona f = E / h.

Korpuskularno-falowa natura materii jest jednym z głównych wyników mechaniki kwantowej: każdy obiekt materialny może przejawiać naturę falową, co oznacza, że może podlegać zjawiskom dyfrakcji i interferencji. Na przykład można obliczyć, że dla człowieka o masie 50 kg poruszającego się z prędkością 10 km/h długość fali materii równa jest

Heisenberga zasada nieoznaczoności, fundamentalna zasada fizyki kwantowej mówiąca o tym, że iloczyn niepewności jednoczesnego poznania pewnych wielkości (zwanych kanonicznie sprzężonymi w sensie formalizmu hamiltonowskiego: np. chwilowych wartości pędu p i położenia x, energii E i czasu jej pomiaru t, współrzędnej kątowej ϕ leżącej w płaszczyźnie xy i składowej J_z krętu, itd.) nie może być mniejszy od stałej Plancka h podzielonej przez podwojoną liczbę π: ΔxΔp≥h, ΔEΔt≥h, ΔϕΔJ_z≥h, (h=h/2π=1,0545·10^-34J·s).

Mała wartość liczbowa stałej Plancka powoduje, że zasada nieoznaczoności jest istotna głównie dla mikroświata, wiąże się z dualizmem korpuskularno-falowym.

20. Postulaty Bohra:

1. Kiedy elekton krąży po jednej z dozwolonych orbit i nie promieniuje energii w postaci fal elektromagnetycznych. Energia jest emitowana podczas przeskoku elektronu z jednej z dozwolonych orbit na inną.

2. Dla elektronu krążącego wokół jądra dozwolone są tylko takie orbity, dla których moment pędu, zwany inaczej krętem (będący iloczynem pędu elektronu i promienia orbity, po której krąży), jest całkowitą wielokrotnością stałej Plancka podzielonej przez 2π.

Liczby kwantowe:

1) Główna liczba kwantowa (n)
- przyjmuje wartości kolejnych liczb naturalnych 1, 2, 3, ... (wg Bhora K, L, M, ...);
- od niej zależy energia danego elektronu;
- decyduje o rozmiarach orbitali - im większa wartość n, tym większy jest orbital;
- maksymalna ilośc elektronów w powłoce wynosi 2m2 (kwadrat)
1 = K
2 = L
3 = M
4 = N
5 = O
6 = P
7 = Q
2) Poboczna liczba kwantowa (l)
- przyjmuje wartości liczb całkowitych od 0 do n-1 włącznie;
- precyzuje dokładniej stan energetyczny danej powłoki;
- liczba stanów kwantowych wyraża się wzorem 4l + 2
0 = s
1 = p
2 = d
3 = f
4 = g
5 = h
6 = i
3) Magnetyczna liczba kwantowa (m)
- przyjmuje wartości liczb całkowitych takich, że -1 jest mniejsze bądz równe n, które jest mniejsze badz równe +1;
- określa rzut momentu pędu na wyróżniony kierunek;
- decyduje o wzajemnych ułożeniu orbitali w przestrzeni
4) Magnetyczna spinowa liczba kwantowa (ms)
- charakteryzuje rut spinu na wyróżniony kierunek w przestrzeni;
- może przyjmowac tylko dwie wartości +1/2 lub -1/2

Zakaz Pauliego głosi, że w danym stanie kwantowym może znajdować się jeden fermion - albo inaczej, że żadne dwa fermiony nie mogą w jednej chwili występować w dokładnie tym samym stanie kwantowym.

21. Doświadczenie Francka-Hertza wykonane w 1913 roku przez dwóch niemieckich fizyków, które po raz pierwszy wykazało istnienie wzbudzonych stanów atomów o nieciągłych wartościach energii. Doświadczenie polegało na przepuszczeniu prądu przez trójelektrodową lampę składającą się z anody, katody i siatki. Przy tym źródła prądu były tak podłączone, że stałe napięcie między siatką a anodą miało własności hamujące dla elektronów przyspieszanych na drodze od katody do siatki. Przy zwiększaniu napięcia przyspieszającego między katodą i siatką okazało się, że prąd płynący przez rozrzedzony gaz w lampie wykazywał szereg maksimów i minimów. Na gruncie fizyki klasycznej efektu tego nie można było wyjaśnić. Istnienie nieciągłych poziomów energetycznych w atomach gazu tłumaczy minima prądu I (V) w taki sposób, że przy pewnej wartości napięcia elektrony przyspieszone uzyskują energię równą różnicy energii między pierwszym poziomem w atomie a poziomem podstawowym. Są one zatem w stanie wzbudzić atom tracąc same energie, co przejawia się spadkiem natężenia prądu płynącego przez lampę (obserwowane minimum funkcji I (V))

22. Funkcja falowa, podstawowa wielkość opisująca stan układu kwantowego (położenie cząstki w przestrzeni w danej chwili czasu) w ujęciu nierelatywistycznym lub w prostych układach relatywistycznych (np. cząstka swobodna lub w słabym polu).
Opis ma charakter probabilistyczny. Kwadrat modułu funkcji falowej dla danych wartości zmiennych określa prawdopodobieństwo znalezienia układu w stanie określonym przez te zmienne.
Funkcja falowa jest dana funkcją zespoloną, określona jest z dokładnością do fazy. W ujęciu nierelatywistycznym funkcja falowa spełnia równanie Schrödingera (w relatywistycznym, np. równanie Diraca).

Schrödingera równanie, podstawowe równanie mechaniki kwantowej sformułowane w 1926 przez E. Schrödingera (zgodne z tzw. obrazem Schrödingera). Ogólnie Schrödingera równanie ma postać:

gdzie: i - jednostka urojona, h = h/2π (h - stała Plancka), t - czas, H - hamiltonian układu, ψ - funkcja falowa opisująca ten układ.

Schrödingera równanie opisuje układy kwantowe przy pominięciu ich własności wynikających z ułamkowych wartości spinów cząstek oraz efektów relatywistycznych. Stosuje się je do opisu atomu wodoru, a także (w przybliżeniu) bardziej złożonych atomów oraz zjawisk kwantowych w kryształach. Schrödingera równanie opisujące niezależną od czasu radialną strukturę atomu wodoru ma postać:

gdzie: ∇² - kwadrat operatora nabla, µ - masa zredukowana elektronu i jądra atomowego, U - energia potencjalna elektronu w polu elektromagnetycznym jądra, u - część funkcji falowej zależna jedynie od wzajemnego położenia elektronu i jądra, E - energia układu.

Rozwiązania tego równania, będące złożeniem wielomianów Laguerre'a (opisujących zależność radialną) i funkcji kulistych (opisujących zależności kątowe), odtwarzają z dobrym przybliżeniem strukturę atomu wodoru (m.in. poziomy energetyczne).

24. Oscylator harmoniczny jest układem fizycznym, który ma duże zastosowanie i znaczenie w wielu działach fizyki.

Jest to ciało o masie m, na które działa siła proporcjonalna do wychylenia z przeciwnym zwrotem F = − kx. Ponieważ siła
to układ opisany jest przez potencjał

Jego energia całkowita jest równa

gdzie pęd p = mv. W mechanice kwantowej pęd p przechodzi w operator
spełniający regułę komutacyjną
. Wygodnie jest zdefiniować zamiast x, p dwa operatory

nazywane operatorami anihilacji i kreacji. Stąd operator położenia x to

Tunelowy efekt, zjawisko tunelowe, zjawisko kwantowe polegające na przenikaniu cząstki przez barierę potencjału (co wyklucza fizyka klasyczna). Jedno z dopuszczalnych wyjaśnień efektu tunelowego polega na odwołaniu się do zasady nieoznaczoności: pęd i energia potencjalna cząstki nie dadzą się ściśle określić w tym samym czasie, czyli możliwe są fluktuacje energii pozwalające na pokonanie bariery potencjału.

Innym, obrazowym wyjaśnieniem efektu tunelowego jest przedstawienie owej bariery jako tworu zbudowanego z cząstek wirtualnych: oddziaływanie na nie cząstki przenikającej następuje wówczas zgodnie z pewnym skończonym prawdopodobieństwem.

Efekt tunelowy wyjaśnia wiele procesów fizycznych pozornie tak różnych, jak rozpad alfa czy działanie diody tunelowej.

---