SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ |
||||
KATEDRA TECHNIKI POŻARNICZEJ |
LABORATORIUM HYDROMECHANIKI |
|||
Ćwiczenie nr:13
Temat: „ Badanie procesu zasysania wody” |
Pluton: III |
Imię i nazwisko: Damian Saleta |
||
|
Grupa: B |
|
||
Prowadzący: bryg. mgr inż. Wojciech Zegar |
Data wykonania: 17.02.2002 |
Data złożenia:
|
Ocena: |
|
Cel ćwiczenia
Zastosowane w ćwiczeniu metody pomiarowe pozwalają na określenie charakterystyki pompy próżniowej, charakterystyki nieszczelności, teoretycznego czasu ssania i rzeczywistego czasu ssania na podstawie zarejestrowanych nieustalonych przebiegów zmian ciśnienia w rozpatrywanym układzie. W celu opracowania wyników najkorzystniej byłoby wykorzystać możliwości EMC.
Określenie charakterystyk Qp f(∆p) i Qn,=f(∆p)
Naszym celem było określenie charakterystyk pompy próżniowej i nieszczelności metodą graficzną. Rezultatem jest charakterystyka przedstawiona w formie wykresu. Z pomiarów uzyskujemy wykresy ∆p= f(t). Ponieważ wydatek jest w obydwu przypadkach obliczany ze wzoru: ![]()
w którym nie znamy pochodnej dp/dt, zatem musimy zróżnicować graficznie wykresy otrzymane z rejestratora. Konstrukcja punktów wykresu pochodnej opiera się na fakcie, że pochodna jest równa tangensowi kąta nachylenia stycznej do krzywej
Rys. Konstrukcja punktów wykresu pochodnej.
Sposób wyznaczania pochodnej zostanie omówiony na przykładzie punktu M1 rozpatrywanej krzywej. W punkcie M1 prowadzimy styczną do krzywej. Następnie przez punkt M1 prowadzimy prostą równoległą do osi odciętych (oś czasu). Od punktu M1 odmierzamy na tej prostej odcinek x1 równy przykładowo 20 mm (długość tego odcinka jest dowolna, ale najłatwiej przyjąć ją za 10 mm, 20 mm itp.). Przez koniec tak wyznaczonego odcinka (punkt A) prowadzimy prostą prostopadłą aż do przecięcia się ze styczną i oznaczamy punkt przecięcia (punkt B). Mierzymy z dokładnością do 1 mm długość odcinka AB (y1). Wartość pochodnej w punkcie M1 wyznaczamy korzystając z następującego wyrażenia:
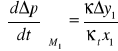
gdzie:
x1 - długość odcinka AM1 w mm,
y1 - długość odcinka AB w mm,
κt - współczynnik skali osi czasu t w s/mm,
κΔp - współczynnik skali osi Δp w hPa/mm,
Stanowisko pomiarowe
Badanie charakterystyki pompy próżniowej możemy przeprowadzi* na stanowisku pomiarowym przedstawionym schematycznie na rysunku. W celu dokonania pomiaru należy zamkną* wszystkie zawory odcinające zbiornik od atmosfery oraz zawór do suchej próżni uniemożliwiający zassanie wody. Cały układ pomiarowy powinien by* hermetyczny. Jego objętość jest znana. Do przygotowanego w opisany wyżej sposób zbiornika przyłączamy pompę próżniową i rejestrujemy proces spadku ciśnienia w czasie Δp = f(t)).
Ponieważ proces ten zachodzi przy stałej objętości a ponadto przy stałej temperaturze, możemy napisać, że ciśnienie powietrza w układzie zależy jedynie od ilości (masy) zawartego w nim powietrza.
Przykładowe obliczenia
Obliczenie stałej „C” potrzebnej do wyznaczenia wydatku „Q”.
p∙V = m∙R∙T
ponieważ: m = C∙p, to ![]()
gdzie: V - objętość zbiornika = 70∙10-3 [m3],
R - stała gazowa = 287 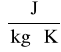
T - temperatura = 293 [K]
C = 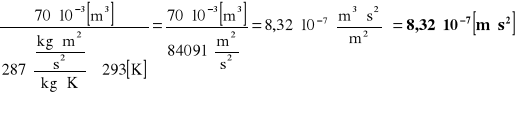
Obliczenie pochodnej w danym punkcie dla pompy pracującej w układzie szczelnym
![]()
x1=20 mm
y1=33 mm
![]()
Obliczenie wydatku „Q”
Q = ![]()
gdzie:
C - stała,
![]()
- wartość pochodnej wyznaczonej metodą graficzno - obliczeniową
Q = 8,32∙10-7[m∙s2]∙1,65 [hPa/s] = 13,73∙10-5[Pa∙m∙s] =
13,73 ⋅ 10-5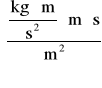
= 13,73∙10-5![]()
Tabele obliczeniowe
Dla pompy pracującej w układzie szczelnym
Lp. |
Δp [hPa] |
|
|
200 |
1,65 |
13,73 ∙ 10-5 |
|
400 |
1,15 |
9,57 ∙ 10-5 |
|
600 |
0,60 |
4,99 ∙ 10-5 |
|
700 |
0,35 |
2,91 ∙ 10-5 |
|
800 |
0,15 |
1,25 ∙ 10-5 |
Obliczenie pochodnej w danym punkcie dla pompy pracującej w układzie ze średnią nieszczelnością
![]()
x1=20 mm
y1=9 mm
![]()
Dla pompy pracującej ze średnią nieszczelnością
Lp. |
Δp [hPa] |
|
|
800 |
0,45 |
3,74 ∙ 10-5 |
|
700 |
0,35 |
2,91 ∙ 10-5 |
|
500 |
0,40 |
3,33 ∙ 10-5 |
|
400 |
0,40 |
3,33 ∙ 10-5 |
|
300 |
0,35 |
2,91 ∙ 10-5 |
Q = 8,32∙10-7[m∙s2]∙0,45 [hPa/s] = 3,74∙10-5[Pa∙m∙s] =
3,74 ⋅ 10-5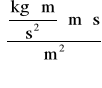
= 3,74∙10-5![]()
Obliczenie pochodnej w danym punkcie dla pompy pracującej w układzie z małą nieszczelnością
![]()
x1= 10 mm
y1= 18 mm
![]()
Dla pompy pracującej z mała nieszczelnością
Lp. |
Δp [hPa] |
|
|
700 |
1,80 |
14,97 ∙ 10-5 |
|
500 |
1,70 |
14,14 ∙ 10-5 |
|
300 |
1,20 |
9,98 ∙ 10-5 |
|
200 |
1,10 |
9,15 ∙ 10-5 |
|
100 |
0,80 |
6,65 ∙ 10-5 |
Q = 8,32∙10-7[m∙s2]∙1,80 [hPa/s] = 14,97∙10-5[Pa∙m∙s] =
14,97 ⋅ 10-5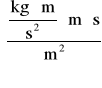
= 14,97∙10-5![]()
Wnioski
Z otrzymanych danych wynika, że wraz ze wzrostem podciśnienia maleje wydajność pompy a rośnie ilość powietrza zasysanego przez nieszczelności układu. Dla różnych nieszczelności sporządzone zostały charakterystyki Qn = f(∆p). Maksymalne podciśnienie jakie może wytworzyć pompa przedstawia punkt przecięcia wykresu Qp = f(∆p), z wykresem Qn = f(∆p), przy danej nieszczelności. Przy wprowadzeniu do układu nieszczelności zauważyliśmy wzburzenie słupa wody w linii ssawne. Na podstawie przeprowadzonego ćwiczenia należy stwierdzić, że podciśnienie maksymalne jest tym niższe im większa jest nieszczelność. Stosunkowo mała dokładności metody wyznaczania pochodnej wynika z różnic pomiędzy maksymalnymi podciśnieniami zarejestrowanymi podczas przeprowadzania ćwiczenia, a wyznaczonymi na wykresie. Na podstawie otrzymanych danych sporządzone zostały charakterystyki Qp = f(∆p), oraz Qn = f(∆p).
SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ - LABORATORIUM HYDROMECHANIKI
Wyszukiwarka