LABORATORIUM FIZYKI 1 |
Ćwiczenie nr: 12 |
|||
|
Data: |
|||
Wydział: WIP |
Grupa: A-23 |
Zespół: 5 |
Punktacja: |
Przygotowanie: |
Nazwisko i imię: Dmitriew Adam |
|
|
||
|
|
Sprawozdanie: |
||
Temat ćwiczenia:
Badanie procesów relaksacyjnych w obwodach elektrycznych |
|
|
||
|
|
Suma punktów: |
||
Cel ćwiczenia:
Wyznaczenie napięcia zapłonu Uz i gaśnięcia Ug neonówki podlączonej do układu
Badanie zależności okresu drgań od wartości oporności R i pojemności C w układzie.
1. Pomiar napięcia zapłonu Uz i napięcia gaśnięcia Ug neonówki.
Część teoretyczna:
Neonówka, lampa neonowa - wynaleziona w 1909 przez Francuza Georgesa Claude- najprostsza lampa wyładowcza w postaci dwóch elektrod umieszczonych wewnątrz szklanej bańki wypełnionej gazem szlachetnym (zazwyczaj neonem lub mieszaniną gazów). W zależności od składu i ciśnienia gazu w bańce, oraz od powierzchni, kształtu i odległości elektrod napięcia zapłonu w takiej lampie są różne i wynoszą od około 60 V do kilku kilowoltów. Przekroczenie tego napięcia powoduje świecenie jonów gazu wokół tej z elektrod, która ma potencjał ujemny (katody), natomiast gaz wokół anody pozostaje ciemny. Przyłożenie do neonówki napięcia przemiennego powoduje cykliczne zamienianie się rolami anody i katody i w efekcie rozbłyskanie gazu na przemian wokół obu elektrod. Od składu mieszaniny gazów zależy także kolor światła - zazwyczaj jest on pomarańczoworóżowy. Po zapłonie gazu w neonówce prąd wzrasta, ale w typowych neonówkach nie przekracza maksymalnie kilku miliamperów. Jeśli w obwodzie neonówki jest włączony szeregowy rezystor, to napięcie na elektrodach lampy stabilizuje się na poziomie poniżej napięcia zapłonu.
Część obliczeniowa:
Przed przystąpieniem do pomiarów, należy złożyć układ według wyżej podanego schematu. Do układu podłączono zasilacz laboratoryjny, opornik o wartości R=50 kΩ oraz woltomierz. Po podłączeniu układu, przystępujemy do pomiaru. W miarę zwiększania napięcia, doprowadzamy do sytuacji, w której przy odpowiednim napięciu zapala się neonówka. Odczytujemy najwyższą wartość napięcia przed zapłonem, ponieważ w momencie zaświecenia napięcie spada o kilka woltów. Następnie powoli obniżamy napięcie na zasilaczu, aż do momentu zgaśnięcia neonówki Ug. Zapisujemy wartość Ug. Pomiar przeprowadzamy 6 krotnie. Wyniki pomiarów przedstawia poniższa tabelka:
N U [V] |
1 |
2 |
3 |
4 |
5 |
6 |
U śr |
Uz |
74,5 |
74 |
75 |
75 |
75,5 |
74,5 |
74,75 |
Ug |
57,5 |
56 |
56,5 |
57 |
57,5 |
57 |
56,91 |
Z poniższych pomiarów wyliczamy średnią Uz i Ug z poniższych wzorów:
Następnie obliczamy błąd systematyczny dla napięcia zapłonu Uz i napięcia gaśnięcia Ug neonówki. W tym celu skorzystamy z poniższych danych oraz wzorów:
Klasa woltomierza: 0,5 Liczba działek: 30 Zakres: 150 [v] Wartość oporu opornika: 50 kΩ
Ostatnią czynnością jest obliczenie błędu przypadkowego dla napięcia zapłonu Uz i gaśnięcia Ug neonówki. Błąd ten obliczamy z poniższego wzoru:
Całkowity błąd ∆Uz: ∆Uz = δz + Suz = ±1,2744 [V]
Całkowity błąd ∆Ug: ∆Ug = δg + Sug = ±1,3345 [V]
Wartość Uz = 74,75 ±1,27 [V] Wartość Ug = 56,91 ±1,34 [V]
2)Badanie zależności okresu drgań od wartości oporności R i pojemności C kondensatora.
Do przeprowadzenia tej części ćwiczenia potrzebne jest złożenie układu którego budowa jest ukazana powyżej. W przypadku gdy napięcie na zasilaczu jest stałe, niepotrzebne jest podłączanie dodatkowego woltomierza. Pomiary wykonujemy dla różnych wartości oporu opornika (300, 380, 470, 560, 570, 722, 850 kΩ) i różnych wartości pojemności kondensatora ( 2, 1, 0,1 μF). Następnie obliczaliśmy czas 20 rozbłysków neonówki dla różnych wartości opornika i kondensatora, co przedstawia poniższa tabela (pomiar był wykonywany dwoma stoperami, każdy z dokładnością 0,01 [s]) :
C [μF] |
R [kΩ] |
t20 [s] |
∆R [kΩ] |
∆C [μF] |
T eksp [s] |
C1 = 2 μF |
300 |
34,50/34,41 |
30 |
0,2 |
1,72275 |
|
380 |
42,06/41,88 |
38 |
0,2 |
2,0985 |
|
470 |
53,68/53,82 |
47 |
0,2 |
2,6875 |
|
560 |
61,50/61,50 |
56 |
0,2 |
3,075 |
|
570 |
61,68/61,80 |
57 |
0,2 |
3,087 |
|
722 |
79,42/79,50 |
72,2 |
0,2 |
3,973 |
|
850 |
92,92/92,94 |
85 |
0,2 |
4,6465 |
C2 = 1 μF |
300 |
17,38/16,86 |
30 |
0,1 |
0,856 |
|
380 |
20,80/20,80 |
38 |
0,1 |
1,04 |
|
470 |
26,44/26,30 |
47 |
0,1 |
1,3185 |
|
560 |
30,38/30,32 |
56 |
0,1 |
1,5175 |
|
570 |
30,76/30,88 |
57 |
0,1 |
1,541 |
|
722 |
39,82/40,08 |
72,2 |
0,1 |
1,9975 |
|
850 |
47,80/47,64 |
85 |
0,1 |
2,386 |
C3 = 0,1 μF |
300 |
3,14/3,11 |
30 |
0,01 |
0,15625 |
|
380 |
4,56/4,90 |
38 |
0,01 |
0,2365 |
|
470 |
5,43/5,64 |
47 |
0,01 |
0,27675 |
|
560 |
6,35/6,44 |
56 |
0,01 |
0,31975 |
|
570 |
6,58/6,50 |
57 |
0,01 |
0,327 |
|
722 |
7,67/7,56 |
72,2 |
0,01 |
0,38075 |
|
850 |
8,56/8,64 |
85 |
0,01 |
0,43 |
Pojedynczy okres T eksp obliczamy ze wzoru:
Następnie obliczamy ∆R ze wzoru: ∆R = ±10%*R=0,1*R , ∆C ze wzoru:
∆C = ±10%*R=0,1*C a ∆U dla napięcia U = 77,2 [V] wynosi ∆U = ±0,7 [V]
Wartości ∆Uz i ∆Ug odczytujemy z poprzedniego punktu sprawozdania.
Mając obliczoną doświadczalną wartość okresu Teksp , wyznaczamy błąd mierzonej wartości.
Błąd ∆ Teksp wynosi: ∆Teksp=±0,3 [s].
Wartość okresu teoretycznego Tteore obliczamy ze wzoru T= t1+t2, gdzie t1- czas ładowania, natomiast t2 - czas rozładowywania. Ponieważ jednak t2 jest bliskie zeru, można zapisać:
T= t1. Wzór na czas t1 znajdujemy poniżej:
gdzie K:
Wartości okresu teoretycznego Tteor wyliczamy dla wszystkich pojemności kondensatora C, oraz wszystkich wartości opornika R. Wyniki przedstawia poniższa tabelka:
C [μF] |
R [kΩ] |
t20 [s] |
Teksp [s] |
Tteor[s] |
C1 = 2 μF |
300 |
34,50/34,41 |
1,7227 |
1,4684 |
|
380 |
42,06/41,88 |
2,0985 |
1,8066 |
|
470 |
53,68/53,82 |
2,6875 |
2,2871 |
|
560 |
61,50/61,50 |
3,075 |
2,7063 |
|
570 |
61,68/61,80 |
3,087 |
2,7221 |
|
722 |
79,42/79,50 |
3,973 |
3,5212 |
|
850 |
92,92/92,94 |
4,6465 |
4,110 |
C2 = 1 μF |
300 |
17,38/16,86 |
0,856 |
0,690 |
|
380 |
20,80/20,80 |
1,04 |
0,892 |
|
470 |
26,44/26,30 |
1,3185 |
1,1016 |
|
560 |
30,38/30,32 |
1,5175 |
1,3126 |
|
570 |
30,76/30,88 |
1,541 |
1,3360 |
|
722 |
39,82/40,08 |
1,9975 |
1,6926 |
|
850 |
47,80/47,64 |
2,386 |
1,9924 |
C3 = 0,1 μF |
300 |
3,14/3,11 |
0,15625 |
0,07132 |
|
380 |
4,56/4,90 |
0,2365 |
0,09123 |
|
470 |
5,43/5,64 |
0,27675 |
0,11283 |
|
560 |
6,35/6,44 |
0,31975 |
0,1344 |
|
570 |
6,58/6,50 |
0,327 |
0,1368 |
|
722 |
7,67/7,56 |
0,38075 |
0,17328 |
|
850 |
8,56/8,64 |
0,43 |
0,204 |
Błąd okresu teoretycznego ∆Tteor wyliczamy ze wzoru różniczki zupełnej, podanej poniżej:
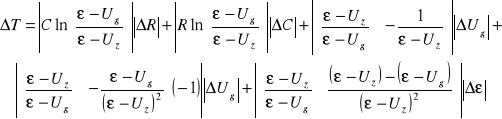
Wyniki pomiarów ∆Tteor przedstawiłem w tabelce powyżej.
C [μF] |
R [kΩ] |
t20 [s] |
Teksp [s] |
∆Teksp[s] |
Tteor[s] |
∆Tteor[s] |
C1 = 2 μF |
300 |
34,50/34,41 |
1,7 |
0,3 |
1,5 |
0,3 |
|
380 |
42,06/41,88 |
2,1 |
0,3 |
1,8 |
0,4 |
|
470 |
53,68/53,82 |
2,7 |
0,3 |
2,3 |
0,5 |
|
560 |
61,50/61,50 |
3,1 |
0,3 |
2,7 |
0,5 |
|
570 |
61,68/61,80 |
3,1 |
0,3 |
2,7 |
0,5 |
|
722 |
79,42/79,50 |
4,0 |
0,3 |
3,5 |
0,8 |
|
850 |
92,92/92,94 |
4,6 |
0,3 |
4,1 |
0,9 |
C2 = 1 μF |
300 |
17,38/16,86 |
0,9 |
0,3 |
0,69 |
0,2 |
|
380 |
20,80/20,80 |
1,0 |
0,3 |
0,89 |
0,24 |
|
470 |
26,44/26,30 |
1,3 |
0,3 |
1,1 |
0,28 |
|
560 |
30,38/30,32 |
1,5 |
0,3 |
1,31 |
0,33 |
|
570 |
30,76/30,88 |
1,5 |
0,3 |
1,34 |
0,34 |
|
722 |
39,82/40,08 |
2,0 |
0,3 |
1,69 |
0,41 |
|
850 |
47,80/47,64 |
2,4 |
0,3 |
1,99 |
0,47 |
C3 = 0,1 μF |
300 |
3,14/3,11 |
0,2 |
0,3 |
0,071 |
0,046 |
|
380 |
4,56/4,90 |
0,2 |
0,3 |
0,091 |
0,076 |
|
470 |
5,43/5,64 |
0,3 |
0,3 |
0,112 |
0,080 |
|
560 |
6,35/6,44 |
0,3 |
0,3 |
0,134 |
0,084 |
|
570 |
6,58/6,50 |
0,3 |
0,3 |
0,137 |
0,085 |
|
722 |
7,67/7,56 |
0,4 |
0,3 |
0,173 |
0,092 |
|
850 |
8,56/8,64 |
0,4 |
0,3 |
0,204 |
0,098 |
Wnioski:
Jak Wynika z powyższych obliczeń wartości teoretyczne okresu drgań relaksacyjnych obwodu różnią się od otrzymanych metodą eksperymentalną. Różnica ta jest wynikiem pominięcia w obliczeniach teoretycznych okresu drgań czasu rozładowywania kondensatora (czasu świecenia neonówki). T=t1+t2 gdzie t1- czas ładowania t2- czas rozładowania. Czas rozładowania jest krótszy od czasu ładowania lecz przy dużej częstotliwości drgań układu odgrywa on znaczącą rolę.
Wyszukiwarka