LABORATORIUM FIZYKI II				Ćwiczenie nr 11
Badanie widma energii promieniowania gamma przy pomocy spektrometru scyntylacyjnego
WIP	Grupa: I-33	Zesp. 1	Data: 29.11.2007
Nazwisko i imię	Przygotowanie	Wykonanie	Sprawdzenie	Suma Punktów
Izbicki Robert
Prowadzący: dr Piotr Kurek

1. Wstęp

Celem ćwiczenia jest obliczenie wartości elementów widm energetycznych widocznych na wykonanym spektrogramie oraz określenie energetycznej zdolności rozdzielczej użytego spektrometru scyntylacyjnego.

Promieniowanie gamma towarzyszy zwykle przemianom jądrowym tj. α, β, których efektem jest m. in. przejście jądra w stan wzbudzenia (X*). Stanowią je kwanty energii o wartości równej różnicy między poziomami energetycznymi jądra przed i po emisji kwantów (fotonów).

Dzięki temu, że przechodząc przez materię, fotony przekazują swoją energię elektronom, zwanym wtórnymi oraz wiedzy o charakterze tych zjawisk możemy budować układy pomiarowe do rejestracji widma energetycznego promieniowania gamma. Fotony przekazują swoją energię elektronom całkowicie lub częściowo i mogą to robić na kilka sposobów, z których najważniejsze są 3: efekt fotoelektryczny, efekt Comptona oraz efekt kreacji (lub anihilacji) pary.

Elektrony wtórne powstałe w wyniku efektu fotoelektrycznego, polegającego na wybiciu elektronu z jego orbity przez foton, całkowicie absorbują foton, a ich energię kinetyczną można obliczyć ze wzoru:

[1]

gdzie: hv - energia absorbowanego fotonu

W_n - energia wiązania elektronu na powłoce

Efektem Comptona nazywamy zjawisko rozpraszania fotonów na elektronach swobodnych. Odrzucone w wyniku tego elektrony mają energię kinetyczną obliczaną ze wzoru:

[2]

gdzie: E_ke - energia kinetyczna elektronu odrzuconego

hv - energia fotonu rozproszonego

hv₀ - energia fotonu przed zderzeniem

Natomiast energię elektronów posiadających jej maksymalną ilość:

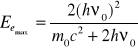
[3]

gdzie: m₀c²=1,02MeV - energia spoczynkowa elektronu

hv₀ - energia fotonu uderzającego w elektron

Efekt kreacji pary polega na utworzeniu pary elektron-pozyton przez foton o odpowiedniej energii, równej co najmniej hv=2 m₀c². Zjawiskiem odwrotnym jest anihilacja pozytonu z elektronem i powstanie w efekcie 2 fotonów o energii 0,51MeV każdy.

2. Układ pomiarowy

Układ pomiarowy składa się z kryształu scyntylacyjnego, fotopowielacza, wzmacniacza liniowego i wielokanałowego analizatora amplitud (WAA).

Rysunek 1: Schemat blokowy spektrometru scyntylacyjnego: SC - scyntylator, FP - fotopowielacz, W - wzmacniacz liniowy, ZWN - zasilacz wysokiego napięcia, WAA - wielokanałowy analizator amplitud, PC - komputer PC.

Fotony promieniowania gamma bombardują kryształ scyntylacyjny posiadający własności luminescencyjne, którym jest nieorganiczny monokryształ jodku sodu aktywowanego talem - NaJ(Tl). elektrony wtórne powstające w trzech omówionych wcześniej zjawiskach generują błyski świetlne, czyli emisję fotonów scyntylacyjnych. Te optyczne sygnały odbierane są przez fotopowielacz, który zbudowany jest z fotokatody, kilku elektrod - tzw. dynod i anody. Fotony scyntylacyjne wybijają z fotokatody fotoelektrony (od 2 do 5 każdy), które są następnie przyspieszane przez szereg dynod, dzięki doprowadzonemu z zasilacza wysokiemu napięciu. Ostatecznie elektrony trafiają na anodę, gdzie generowane są impulsy elektryczne, zamieniane następnie na impulsy napięciowe wzmacniane we wzmacniaczu liniowym. Elementem wieńczącym układ jest wielokanałowy analizator amplitud, który zbiera i segreguje impulsy w zależności od energii i odwzorowuje je w postaci widma energetycznego.

3. Przebieg ćwiczenia

Wykonanie pomiaru składało się z następujących kroków:

1. Włączenie wzmacniacza liniowego i zasilania fotopowielacza.

2. Włączenie komputera z zainstalowaną kartą WAA.

3. Wstawienie do domku i otwarcie pomiarowego pojemnika ze źródłem promieniowania gamma

4. Rozpoczęcie pomiaru i rejestrowania widma energetycznego przez co najmniej 600s.

5. Określenie numerów kanałów i ilości znajdujących się w nich impulsów dla plików absorpcji całkowitej, krawędzi komptonowskich i maksimów rozproszenia wstecznego.

6. Wydrukowanie i opisanie uzyskanego spektrogramu

7. Po wyjęciu i zabezpieczeniu źródła powtórzyć kroki 3-6 dla dwóch pozostałych źródeł.

4. Opracowanie wyników

W miarę upływu czasu spektrogramy stawały się coraz bardziej wyraziste. Widmo stawało się coraz bardziej skupione, zaczęły pojawiać się zauważalne miejsca charakterystyczne wykresów. Po zakończeniu rejestracji widma otrzymaliśmy następujące spektrogramy:

Rysunek 2: Widmo energetyczne kobaltu-60

Na podstawie diagramów zamieszczonych w instrukcji do ćwiczenia dokonaliśmy rozpoznania przedstawionych widm.

Rysunek 3: Spektrogram przedstawiający widmo energetyczne cezu-137

Rysunek 4: Widmo energetyczne sodu-22

Korzystając z diagramu dołączonego do instrukcji ćwiczenia określiłem pik absorpcji całkowitej 1 i 2 dla kobaltu-60. Wynoszą one odpowiednio: 1,17MeV i 1,33MeV. Następnie korzystając z wzoru [3] obliczyłem teoretyczne wartości krawędzi Comptona 1:

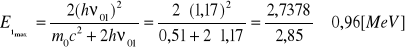
oraz 2:

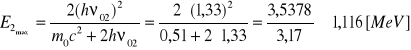
Do wyznaczenia teoretycznej energii piku rozproszenia wstecznego użyłem wzoru [2] Otrzymane wartości to:

Następnie przy pomocy narzędzia Screen Reader programu Microcal Origin odczytałem z wykresu wartości z osi odciętych odpowiadające punktom charakterystycznym. Wartości te są numerami kanałów.

Wartości teoretyczne dla pozostałych pierwiastków określili koledzy analogicznie do wyżej przedstawionego algorytmu. Tak uzyskane dane nanieśliśmy do tabeli protokołu:

Tabela 1: Wartości teoretyczne i doświadczalne charakterystycznych elementów widm energetycznych badanych pierwiastków emitujących promieniowanie gamma.

Cs-137	Wartość teoretyczna [MeV]	nr kanału	Wartość doświadczalna [MeV]
pik absorpcji całkowitej	0,66	1530	0,654
krawędź Comptona	0,476	1154	0,475
pik rozproszenia wstecznego	0,184	490	0,163
Co-60	Wartość teoretyczna [MeV]	nr kanału	Wartość doświadczalna [MeV]
pik absorpcji całkowitej 1	1,17	2600	1,155
pik absorpcji całkowitej 2	1,33	2962	1,325
krawędź Comptona 1	0,96	2200	0,967
krawędź Comptona 2	1,116
pik rozproszenia wstecznego 1	0,21		530	0,182
pik rozproszenia wstecznego 2	0,214
Na-22	Wartość teoretyczna [MeV]	nr kanału	Wartość doświadczalna [MeV]
pik absorpcji całkowitej	1,28	2900	1,296
krawędź Comptona	1,067	2400	1,061
pik rozproszenia wstecznego	0,213	600	0,215
pik absorpcji całkowitej (anihil.)	0,51	1180	0,488
krawędź Comptona (anihil.)	0,34	866	0,340
pik rozproszenia wstecznego (anihil.)	0,17	505	0,170

Aby znaleźć równanie prostej kalibracyjnej prowadzący ćwiczenie wskazał 3 punkty, na podstawie których za pomocą programu Microcal Origin wyznaczyłem metodą najmniejszych kwadratów następujące równanie prostej kalibracyjnej:

[4]

gdzie: E - energia w [MeV]

X - numer kanału

Jak widać na rys. 5 współczynnik korelacji jest bardzo bliski 1, a błąd regresji bardzo mały, więc otrzymaliśmy niemal dokładną zależność liniową wartości energii od numeru kanału.

Tabela 2: Punkty kalibracyjne dla detektora NaI(Tl)

punkt kalibracyjny	Wartość teoretyczna [MeV]	nr kanału
pik absorpcji całkowitej 1 dla Co-60	1,17	2600
pik absorpcji całkowitej 2 dla Co-60	1,33	2962
pik absorpcji całkowitej dla Cs-137	0,184	490

Rysunek 5: Wykres prostej kalibracyjnej dla detektora NaI(Tl)

Na podstawie wzoru [4] przeprowadziłem w arkuszu kalkulacyjnym obliczenia mające na celu znalezienie wartości doświadczalnych do tabeli 1:

Rysunek 6: Arkusz kalkulacyjny programu MS Excel zawierający obliczenia wartości doświadczalnych.

W celu określenia energetycznej zdolności rozdzielczej wybrałem 1 spektrogram: Cs-137 i z jego wykresu odczytałem dane potrzebne do obliczenia tej wartości z równania:

%

5. Rachunek błędów

Program Microcal Origin gotowe wartości błędów dla parametrów δA i δB prostej kalibracyjnej spektrometru. Aby znaleźć wartość błędów δE dla każdej wartości doświadczalnej z tabeli 1 należy zsumować wartość błędu A oraz iloczynu numeru kanału X i wartości błędu parametru B:

[5]

Dodatkowym istotnym błędem jest błąd odczytu wartości z wykresu przeze mnie. Oko ludzkie nie jest tak sprawne, by dokładnie zlokalizować punkt charakterystyczny na wykresie, co generuje poważny błąd, mimo że narzędzie Screen Reader w programie Microcal Origin pokazuje współrzędne wskazanego punktu z dokładnością do 5 miejsc dziesiętnych, a dla wartości wyliczanej nawet więcej.

6. Wnioski

1. Doświadczenie pokazało, że na spektrogramie da się w sposób dość precyzyjny wskazać elementy charakterystyczne widma tj. fotopiki, krawędź Comptona czy pik rozproszenia wstecznego, nawet nie znając teoretycznych wartości tych punktów.

2. W przypadku, gdy widmo jest nieco bardziej skomplikowane (występują różne piki tej samej kategorii) nie jesteśmy w stanie rozróżnić ich na wykresie, bez odpowiednich obliczeń. Wynika to z kiepskiej rozdzielczości energetycznej urządzenia (prawie 10%). Im dokładniejsze urządzenie tym precyzyjniej potrafi wskazać wartość energii dla punktu charakterystycznego.

3. Istotne znaczenie dla jakości pomiaru ma czas pomiaru. W mojej ocenie użyliśmy zbyt krótkiego czasu ekspozycji, co spowodowało dodatkowe rozmycie spektrogramów.

Jedna z tych krawędzi jest na wykresie niewidoczna w związku z tym, nie jesteśmy w stanie przed dokładnymi obliczeniami stwierdzić, dla której krawędzi odczytaliśmy numer kanału.

Wartości teoretyczne są tak zbliżone do siebie, że wykres spektrum zlewa się w tym miejscu w jedno.

Fizyka2. Sprawozdanie z laboratorium Ćwiczenie 11: Spektrometr scyntylacyjny

Str. 2

---