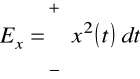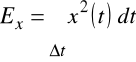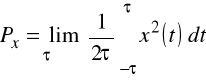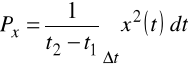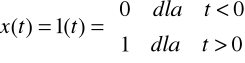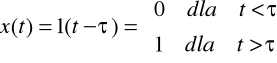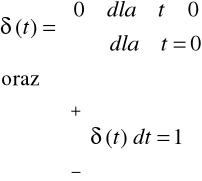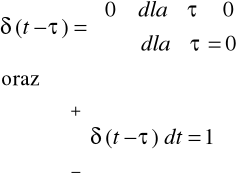2. SYGNAŁY ELEKTRYCZNE ZDETERMINOWANE I ICH WYBRANE MODELE MATEMATYCZNE

2.1. WPROWADZENIE

W teorii obwodów elektrycznych

FUNKCJE opisujące zmienność w czasie wielkości elektrycznych nazywamy przebiegami czasowymi tych wielkości lub SYGNAŁAMI.

Sygnały związane z obwodem elektrycznym są funkcjami czasu t określonymi w pewnej dziedzinie.

Dziedziną sygnałów rozpatrywanych w teorii obwodów jest: przedział lub (dodatnia półoś liczbowa), co odpowiada przypadkowi, gdy opisywane zjawiska rozpoczynają się w chwili t = 0; lub przedział (cała oś liczbowa), co zwykle odpowiada przypadkowi, gdy opisywane zjawiska trwają długo od chwili początkowej tak, że można je uważać za nie mające swojego początku w czasie.

UWAGA: Nasze rozważania będą obejmowały wyłącznie

sygnały deterministyczne.

2.2. KLASYFIKACJA I PARAMETRY SYGNAŁÓW

SYGNAŁY

Energia Ex sygnału x:

jest nieskończona lub nieokreślona

jest skończona

dla sygnałów o nieskończonym czasie trwania

dla sygnałów impulsowych Dla sygnału o czasie trwania Δ t∈(t1, t2)

Moc średnia Px sygnału x

jest skończona.

O OGRANICZONEJ MOCY

O OGRANICZONEJ ENERGII

Jeżeli warunek okresowości

Gdy liczba T jest okresem sygnału x(t), to każda liczba kT (k∈N) jest też okresem tego sygnału. Najmniejszą spośród liczb T spełniającą równość nazywamy okresem właściwym.

jest spełniony

nie jest spełniony

OKRESOWE

NIEOKRESOWE

HARMONICZNE

ODKSZTAŁCONE

PARAMETRY CHARAKTERYZUJĄCE

SYGNAŁY OKRESOWE

Dla sygnału okresowego x o wartościach x(t):

• Moc średnia

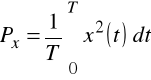
(2.1)

• Wartość maksymalna - największa wartość chwilowa jaką sygnał osiąga - oznaczamy ją jako X_m

• Wartość średnia całookresowa (jest to średnia arytmetyczna tego sygnału obliczona za jeden okres)

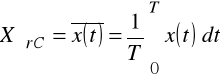
(2.2)

• Wartość średnia półokresowa (jest to średnia arytmetyczna tego sygnału obliczona za połowę okresu)

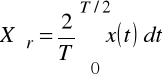
(2.3)

• WARTOŚĆ SKUTECZNA (jest to pierwiastek kwadratowy z wartości średniej kwadratu sygnału obliczonej za jeden okres, inaczej - pierwiastek kwadratowy ze średniej mocy sygnału)

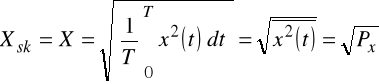
(2.4)

2.3. SKOK JEDNOSTKOWY, DELTA DIRACA

W analizie obwodów elektrycznych ważną rolę spełniają dwa rodzaje sygnałów, opisanych przez funkcję jednostkową i dystrybucję Diraca.

SKOK JEDNOSTKOWY

Funkcja skoku jednostkowego, zwana też skokiem jednostkowym, oznaczana przeważnie przez 1(t) - określana jest następująco:

(2.5)

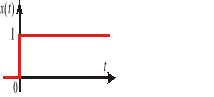
Rys.2.1. Skok jednostkowy

Ze wzoru (2,5) wynika, że w chwili t = 0 pojawia się sygnał o wartości „jeden” i następnie dla czasów t > 0 nie ulega on zmianie (rys.2.1). Każde wymuszenie stałe doprowadzone do obwodu w chwili t = 0 można traktować jako iloczyn sygnału jednostkowego i wielkości stałej.

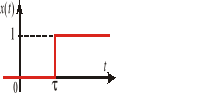
Jeśli skok jednostkowy pojawia się z opóźnieniem, np. τ (rys.2.2), to mamy do czynienia ze skokiem jednostkowym opóźnionym (przesuniętym) oznaczonym 1(t-τ) i opisanym wzorem (2.6)

(2.6)

Rys.2.2. Skok jednostkowy przesunięty

DELTA DIRACA

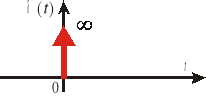
Funkcję dystrybucji Diraca δ(t), zwaną też uogólnioną funkcją δ(t), deltą Diraca (rys.2.3) definiujemy następująco:

(2.7)

Rys.2.3. Delta Diraca

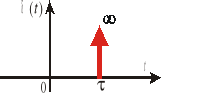
Jeśli w równaniach (2.7) w miejsce t wstawimy (t-τ) otrzymamy deltę Diraca przesuniętą o τ (rys.2.4), tj. wielkość δ(t-τ) o własnościach:

(2.8)

Rys.2.4. Delta Diraca przesunięa

2.4. SYGNAŁY HARMONICZNE

W grupie przebiegów okresowych szczególne znaczenie mają sygnały harmoniczne, tzn. cosinusoidalne i sinusoidalne. Ponieważ jednak:

,

nazwiemy je ogólnie sinusoidalnymi (sinusoidalnie-zmiennymi).

Sygnałami harmonicznymi nazywamy sygnały, których przebieg jest sinusoidalną funkcją czasu

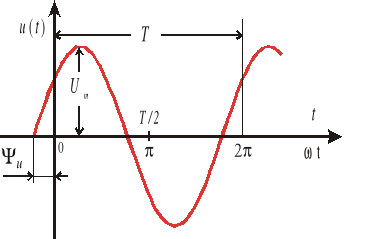
Załóżmy, że rozpatrujemy sygnał sinusoidalny w postaci napięcia:

(2.9)

Rys.2.5.

gdzie: u(t) - wartość chwilowa napięcia;

U_m - wartość maksymalna napięcia (nazywana amplitudą);

- początkowy kąt fazowy, faza początkowa napięcia w chwili t = 0;

- kąt fazowy, faza napięcia w chwili t;

ω =2π f - pulsacja (częstotliwość kątowa) mierzona w rad/s;

f =1/T - częstotliwość mierzona w Hz, będąca odwrotnością okresu.

W czasie odpowiadającym jednemu okresowi faza napięcia zmienia się o 2π, tzn.
. Na rys. 2.5. na osi odciętych oznaczono skalę czasu i skalę kątową.

Wartość średnia (półokresowa) napięcia sinusoidalnego wynosi wg wzoru (2.3)

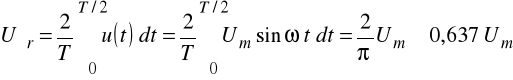
(2.9)

Wartość skuteczna napięcia sinusoidalnego zgodnie ze wzorem (2.4) wynosi

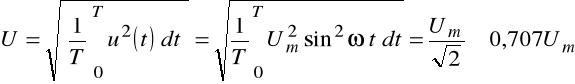
(2.10)

Oznacza to, że równanie chwilowe opisujące napięcie harmoniczne możemy przedstawić w postaci:

(2.11)

2.5. SYGNAŁ WYKŁADNICZY

Funkcja wykładnicza jest traktowana w teorii obwodów w sposób szczególny. Wynika to stąd, że:

• każdy sygnał występujący w praktyce może być zawsze wyrażony w postaci sumy funkcji wykładniczych;

• w przypadku obwodów liniowych odpowiedź obwodu na wymuszenie wykładnicze jest także wykładnicza.

Przyjmijmy, że sygnał wykładniczy ma postać:

(2.12)

Współczynnik s występujący w wykładniku jest zespolony

(2.13)

a zatem
(2.14)

Rozpatrzmy szczególne przypadki w zależności od tego jakie wartości przyjmuje s.

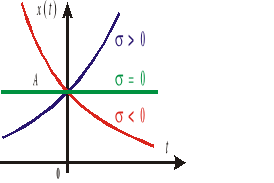
1. Jeżeli s jest liczbą rzeczywistą (tzn. ω = 0) wtedy i ma charakter zależny od wartości σ (rys.2.6)
gdy σ < 0, sygnał x(t) ma charakter monotonicznie malejącej funkcji czasu; gdy σ = 0, sygnał x(t) jest sygnałem stałym o wartości A; gdy σ > 0, sygnał x(t) ma charakter monotonicznie rosnącej funkcji czasu.	Rys.2.6.

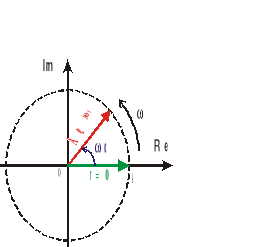
2. Jeżeli s jest liczbą urojoną (tzn. σ=0) wtedy sygnał x(t) może być interpretowany na płaszczyźnie zmiennej zespolonej za pomocą tzw. wektora wirującego (rys.2.7)
obracającego się z prędkością kątową ω w kierunku przeciwnym do ruchu wskazówek zegara. Położenie tego wektora na płaszczyźnie w danej chwili t określone jest za pomocą kąta ωt.	Rys.2.7.
Czynnik spełnia rolę operatora obrotu, natomiast jest modułem wektora.

Uwzględniając wzór Eulera

(2.15)

można wektor wirujący wyrazić za pomocą dwóch składowych

(2.16)

Część rzeczywista wektora wirującego przedstawia sygnał o charakterze cosinusoidalnym

(2.17)

Część urojona wektora wirującego przedstawia sygnał o charakterze sinusoidalnym

(2.18)

Wynika stąd, że najczęściej spotykane przebiegi wielkości elektrycznych stanowią szczególne przypadki sygnału o charakterze wykładniczym.

2.6. OPIS SYMBOLICZNY SYGNAŁU HARMONICZNEGO

Rozpatrzmy ponownie sygnał sinusoidalny w postaci napięcia:

(2.19)

Związek pomiędzy wektorem wirującym na płaszczyźnie zmiennej zespolonej a rozpatrywanym sygnałem sinusoidalnym przedstawia rys.2.8.

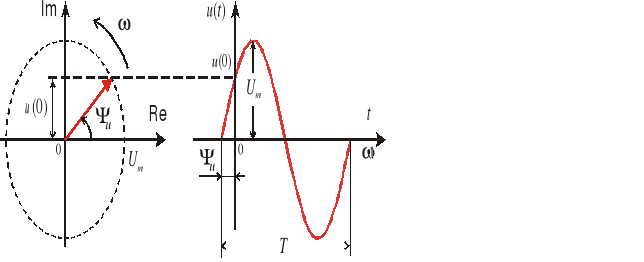
Rys.2.8.

Wartość chwilowa napięcia w chwili t = 0 wynosi

(2.20)

W chwili tej wektor wirujący o amplitudzie U_m jest nachylony względem osi liczb rzeczywistych pod kątem
. Rzut tego wektora na oś liczb urojonych wynosi u(0), czyli wartość chwilowa sygnału sinusoidalnego jest równa rzutowi wektora wirującego na oś liczb urojonych.

Analitycznie można to ująć, zgodnie z zależnością (2.18), następująco:

dla każdej chwili t

(2.21)

Sygnał sinusoidalny:

posiada następującą

POSTAĆ SYMBOLICZNĄ (symboliczną wartość chwilową):

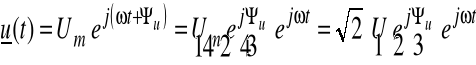
(2.22)

Czyli:

(2.23)

UWAGI:

• 
  

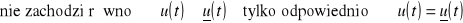
• natomiast:
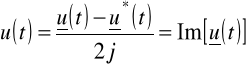
  (2.24)

Metoda symboliczna zapisu przebiegów sinusoidalnych pozwala traktować je jako przebiegi wykładnicze.

- 38 -

- 37 -

wartość skuteczna

amplituda

(wartość max.)

(rzeczywista)

wartość chwilowa

U_m

symboliczna amplituda

/postać zespolona amplitudy/

/wskaz amplitudy/

symboliczna wartość skuteczna

/wskaz wartości skutecznej/

U

---