WAT	Laboratorium z elektrotechniki
Przedmiot:	Elektrotechnika
Grupa szkoleniowa: L9X2S1	Skład grupy: 1.Olga Moniuszko 2.Ewelina Chmielewska 3.Joanna Balcerzak 4.Robert Filiks 5.Michał Musur - L9X3S1	Data wykonania ćw: 8.03.10	Data oddania sprawozdania z ćw:24.03.10
				Prowadzący:	Ocena:
Temat:	Badania liniowych obwodów elektrycznych

1. Cel ćwiczenia :

Celem ćwiczenia jest przypomnienie podstawowych praw rządzących przepływem prądu stałego w obwodach elektrycznych - prawa Ohma i Kirchhoffa - oraz ich weryfikacja poprzez pomiary napięcia, natężenia prądu i rezystancji.

2. Wstęp teoretyczny:

Zadanie I

Polega na sprawdzeniu teoretycznych wyników dla prawa Ohma w obwodzie nierozgałęzionym przy regulowanym napięciu U i przy stałej rezystancji R oraz porównaniu ich z wynikami otrzymanymi podczas doświadczenia.

Rys.1. Schemat badanego układu

Prawo Ohma

Wartość naprężenia prądu I występującego w danym elemencie obwodu elektrycznego jest wprost proporcjonalna do napięcia U na zaciskach tego elementu i odwrotnie proporcjonalna do rezystancji R.

Interpretując to możemy stwierdzić że gdy napięcie wzrasta 2-krotnie, wtedy wywołany tym napięciem przepływ prądu też osiągnie natężenie 2 razy większe, gdy napięcie wzrośnie 5 krotnie, to natężenie prądu też powinno wzrosnąć 5 razy w stosunku do wartości początkowej.

Po przekształceniu tego wzoru można uzyskać inne, równoważne wzory:

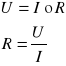
Rys. 2. Charakterystyka prądowo napięciowa przewodnika spełniającego prawo Ohma jest linią prostą.

Bierzemy pod uwagę uogólnione prawo Ohma dotyczące tylko obwodów nierozgałęzionych tzn. takich, w których we wszystkich elementach obwodu występuje ten sam prąd elektryczny. Prawo to jest zależnością miedzy prądem I występującym w obwodzie elektrycznym oraz równoważnym napięciem źródłowym E wszystkich źródeł napięcia w obwodzie .Wartość naprężenia prądu I występującego w obwodzie jest wprost proporcjonalna do wartości sumy algebraicznej wszystkich źródeł napięcia w tym obwodzie i odwrotnie proporcjonalna do rezystancji równoważnej obwodu.

Pomiary			Obliczenia			Błąd pomiaru
U [V]	I [A]	R [Ω]	I [A]	R [Ω]	U [V]	I [A]
1	0,030	33,3	0,030	33,333	0,999	0,000
2	0,060	33,3	0,060	33,333	1,998	0,000
3	0,088	33,3	0,090	34,091	2,930	0,002
4	0,118	33,3	0,120	33,898	3,929	0,002
5	0,148	33,3	0,150	33,784	4,928	0,002
1	0,022	44,4	0,023	45,455	0,977	0,001
2	0,036	54,4	0,037	55,556	1,958	0,001
3	0,046	64,4	0,047	65,217	2,962	0,001
4	0,053	74,4	0,054	75,472	3,943	0,001
5	0,058	84,4	0,059	86,207	4,895	0,001

Tabela 1. Wyniki pomiarów dla prawa Ohma

Wnioski:

Dla obwodu nierozgałęzionego natężenie prądu jest wprost proporcjonalne do przyłożonego napięcia i odwrotnie proporcjonalne do rezystancji. Błędy pomiarowe wynikają z rezystancji wewnętrznej kabli i przyrządów oraz dokładności sprzętu pomiarowego. Natomiast opór danego odbiornika ma wartość stałą. Błąd pomiarowy może wynikać ze zmiany temperatury odbiornika pod wpływem przepływającego przez niego prądu.

Zadanie II

Pierwsze prawo Kirchhoffa:

W dowolnym węźle obwodu suma algebraiczna natężeń prądów wpływających i wypływających do węzła równa się zeru, czyli

Węzłem obwodu nazywamy punkt, w którym łączy się pewna liczba gałęzi obwodu.

Do pomiaru mającego na celu doświadczalne sprawdzenie pierwszego prawa Kirchhoffa wykorzystano:

• źródło napięcia E

• amperomierze (mierniki natężenia prądu) A, A₁, A₂, A₃

• oporniki R₁, R₂, R₃

Rys.3. Schemat badanego układu.

Do obliczeń wykorzystano wzory:

I=I₁+I₂+I₃ [A]

Pomiary								Obliczenia						Błąd pomiaru
U [V]	I [A]	I1 [A]	I2 [A]	I3 [A]	R1 [Ω]	R2 [Ω]	R3 [Ω]	Rz [Ω]	I [A]	U [V]	I1 [A]	I2 [A]	I3 [A]	I [A]	I1 [A]	I2 [A]	I3 [A]
1	0,157	0,086	0,043	0,028	11,1	22,2	33,3	6,055	0,157	0,951	0,086	0,043	0,028	0,000	0,000	0,000	0,000
2	0,325	0,177	0,089	0,059	11,1	22,2	33,3	6,055	0,325	1,968	0,177	0,089	0,059	0,000	0,000	0,000	0,000
3	0,484	0,264	0,133	0,088	11,1	22,2	33,3	6,055	0,485	2,930	0,263	0,132	0,087	0,001	0,001	0,001	0,001
4	0,644	0,352	0,177	0,177	11,1	22,2	33,3	6,055	0,706	3,899	0,290	0,115	0,115	0,062	0,062	0,062	0,062
5	0,799	0,437	0,220	0,146	11,1	22,2	33,3	6,055	0,803	4,838	0,433	0,216	0,142	0,004	0,004	0,004	0,004
1	0,100	0,046	0,030	0,022	21,1	32,2	43,3	9,848	0,098	0,985	0,048	0,032	0,024	0,002	0,002	0,002	0,002
2	0,148	0,063	0,047	0,037	31,1	42,2	53,3	13,403	0,147	1,984	0,064	0,048	0,038	0,001	0,001	0,001	0,001
3	0,177	0,072	0,057	0,047	41,1	52,2	63,3	16,867	0,176	2,986	0,073	0,058	0,048	0,001	0,001	0,001	0,001
4	0,197	0,078	0,064	0,054	51,1	62,2	73,3	20,288	0,196	3,997	0,079	0,065	0,055	0,001	0,001	0,001	0,001
5	0,210	0,081	0,068	0,059	61,1	72,2	83,3	23,684	0,208	4,974	0,083	0,070	0,061	0,002	0,002	0,002	0,002

Tabela 2. Wyniki pomiarów dla I prawa Kirchhoffa

Wnioski:

W obwodzie zamkniętym rozgałęzionym zauważamy, że suma prądów wypływających z węzła I₁, I₂, I₃ nie jest równa prądowi wpływającemu-I. Wynika to z rezystancji wewnętrznej kabli i przyrządów oraz dokładności sprzętu pomiarowego.

A

R

---