Opracowanie: Mateusz Winiarski
WYKŁAD 3
OBLICZANIE CAŁEK Z UŁAMKÓW PROSTYCH II RODZAJU
![]()
całka I1 całka I2

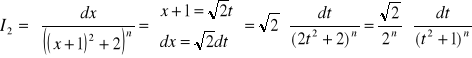
całka In
Wyprowadzenie wzoru rekurencyjnego na In
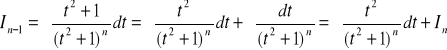
całka I
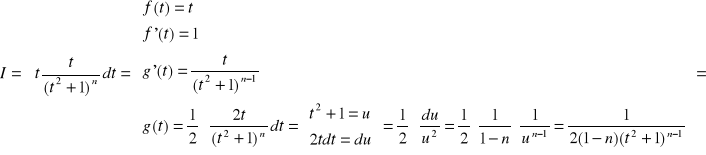
![]()
całka In
![]()
![]()
CAŁKOWANIE FUNKCJI NIEWYMIERNYCH
Metoda współczynników nieoznaczonych Lagrange'a
![]()
gdzie: Vn-1(x) - wielomian stopnia n-1 o nieznanych współczynnikach
![]()
- nieznana liczba
Różniczkując obie strony równania otrzymujemy:
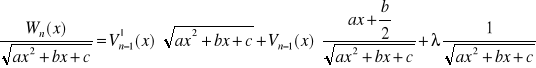
Mnożąc obie strony równania przez ![]()
otrzymujemy:
![]()
Przyrównując współczynniki przy odpowiednich potęgach wielomianów znajdujemy z otrzymanego układu równań nieznane współczynniki wielomianu Vn-1(x) oraz λ.
Pozostaje znaleźć całkę ![]()
. Powyższa całka daje się sprowadzić przez odpowiednie podstawienie do postaci:
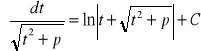
gdy ![]()
![]()
gdy ![]()
PRZYKŁAD 3.1
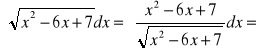
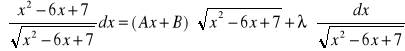
Różniczkując obie strony równania otrzymujemy:
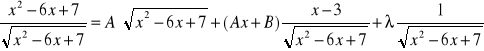
Mnożąc obie strony równania przez ![]()
otrzymujemy:
![]()
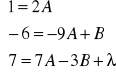
![]()
Czyli:
![]()
całka I1
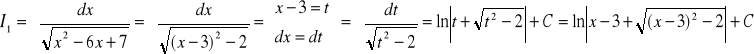
Zatem:
![]()
PRZYKŁAD 3.2

![]()
Podstawienie Eulera
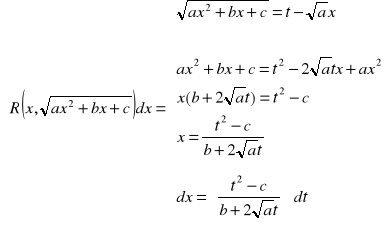
gdzie R jest funkcją wymierną; ![]()
PRZYKŁAD 3.3
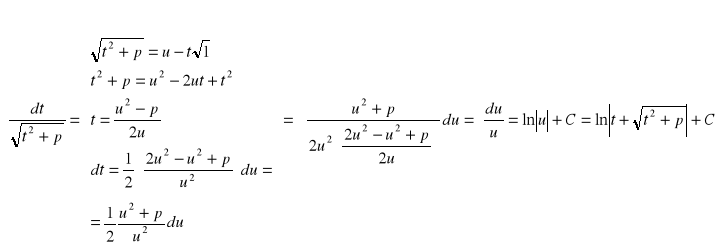
Całka sprowadzalna do typu Lagrange'a
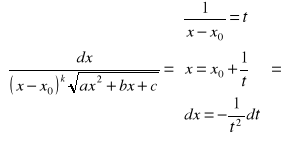
po przekształceniach 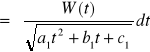
CAŁKOWANIE FUNKCJI NIEWYMIERNYCH c.d.
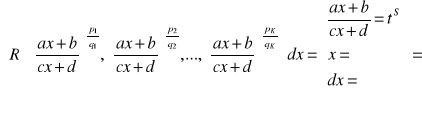
po podstawieniu otrzymujemy całkę z
funkcji wymiernej
gdzie: s - największa wspólna wielokrotność liczb q1,q2,...,qk
PRZYKŁAD 3.4
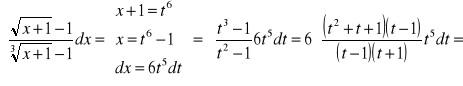
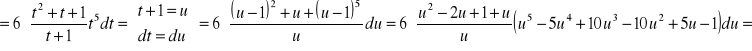
![]()
![]()
CAŁKOWANIE FUNKCJI TRYGONOMETRYCZNYCH
10 ![]()
a) ![]()
(przynajmniej jedna nieparzysta, np. ![]()
)
![]()
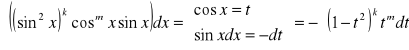
![]()
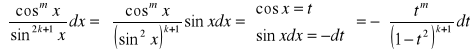
b) ![]()
(obie parzyste)
zasada: zamieniamy na funkcję podwojonego kąta
zał: ![]()
![]()
![]()
wymnażamy i dostajemy całkę tego samego typu
korzystamy ze wzorów: ![]()
; ![]()
; ![]()
PRZYKŁAD 3.5
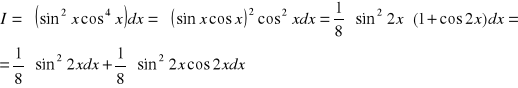
Niech I1 = ![]()
I2 = ![]()
![]()
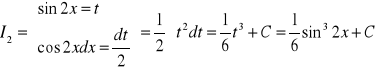
![]()
20
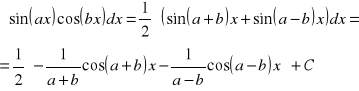
korzystamy ze wzorów:![]()
![]()
![]()
30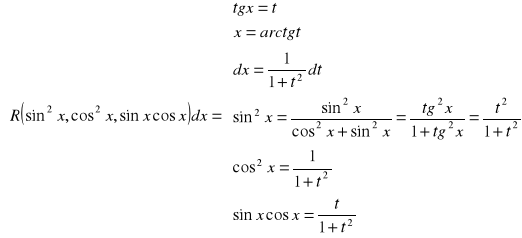
PRZYKŁAD 3.6
![]()
{z 1-ki trygonometrycznej} 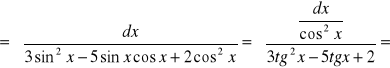
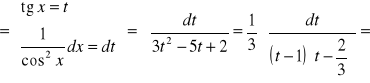
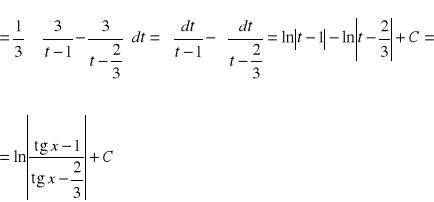
40 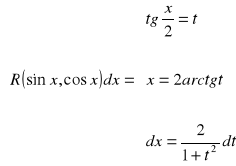
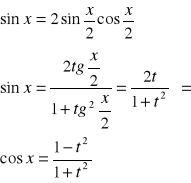
Metoda zasłaniania stosujemy gdy w mianowniku ułamka mamy tylko iloczyn wielomianów stopnia 1 w potędze 1
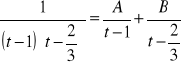

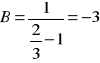
bo: 
dla ![]()

bo: 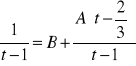
dla ![]()
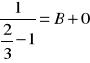
MIARA I CAŁKA
DEFINICJA 3.1 (ILOCZYN KARTEZJAŃSKI)
![]()
- zbiory
![]()
- iloczyn kartezjański zbiorów ![]()
i ![]()
![]()
- zbiory
![]()
- iloczyn kartezjański zbiorów ![]()
DEFINICJA 3.2 (RODZINA PODZBIORÓW)
![]()
- zbiór, ![]()
- zbiór wszystkich podzbiorów![]()
![]()
![]()
![]()
- rodzina podzbiorów zbioru![]()
PRZYKŁAD 3.7
![]()
![]()
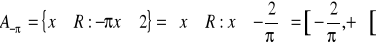
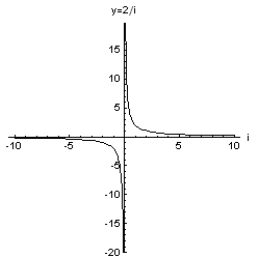
DEFINICJA 3.3 (POŁĄCZENIE, PRZECIĘCIE)
![]()
![]()
![]()
- rodzina podzbiorów zbioru ![]()
![]()
- połączenie zbiorów rodziny ![]()
![]()
- przecięcie zbiorów rodziny ![]()
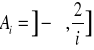
dla ![]()
![]()
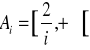
dla ![]()
![]()
Wyszukiwarka