METODY PRZESTRZENI STANÓW

Sposoby przejścia między różnymi opisami

Opis obiektu w przestrzeni stanów nie jest jednoznaczny, tj. różne zestawy macierzy A, b, c mogą opisywać obiekt o tych samych własnościach. Powstaje pytanie jak wybrać wektor stanu mając opis obiektu w postaci transmitancji. Istnieje kilka standardowych sposobów przejścia, które pozwalają na uzyskanie tzw. kanonicznych postaci macierzy A, b, c (metoda bezpośrednia, równoległa, iteracyjna). Weźmy obiekt opisany transmitancją :

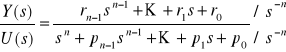
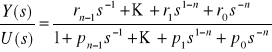
, gdzie

, czyli

.

Rysujemy schemat blokowy wewnętrznej struktury obiektu pamiętając, że mnożenie przez s^-1 oznacza całkowanie.

r_n-1

r_n-2

...... ....

U(s) E(s) Y(s)

∫ ∫ ... ∫ r₀

x_n x_n-1 x₂ x₁

-p_n-1

-p_n-2

.... . . . . .

-p₀

Na poszczególne zmienne stanu x_i (t) wybieramy wielkości :

Po przejściu do dziedziny czasu otrzymuje się układ równań różniczkowych :

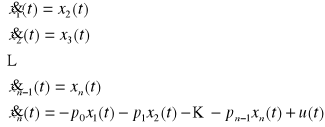
równanie wyjścia :

Wykorzystując zapis macierzowy :

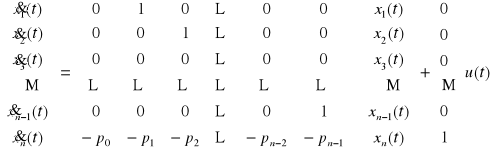
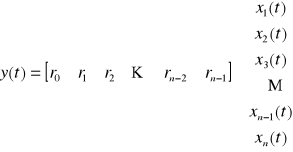
W ten sposób otrzymaliśmy jedną z postaci kanonicznych Brunowsky'ego - Luenbergera macierzy A, b, c. Jest to tzw. postać kanoniczna dla sterowania. Stosując inny tok postępowania można otrzymać tzw. postać kanoniczną dla obserwowania.

;

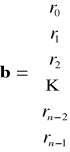
Przejście odwrotne, tzn. z opisu przestrzeni stanów do transmitancji wykonuje się następująco :

Przejście pomiędzy równaniem różniczkowym a transmitancją wykonuje się za pomocą przekształcenia Laplace'a.

Sterowalność i obserwowalność

W przypadku opisu wektorem stanu, może zdarzyć się tak, że przy dostępnym sterowaniu nie jesteśmy w stanie wpływać na niektóre zmienne. Mówimy wtedy, że te zmienne nie są sterowalne. Analogicznie niektóre zmienne stanu mogą w ogóle nie wpływać na wyjście. Mówimy wtedy, że te zmienne nie są obserwowalne. Ogólnie zmienne stanu można podzielić na cztery kategorie.

x - zmienne stanu

sterowalne

i obserwowalne

niesterowalne y(t)

i obserwowalne

u(t) sterowalne

i nieobserwowalne

niesterowalne

i nieobserwowalne

Pojęcie sterowalności i obserwowalności prześledźmy na przykładzie obiektu jakim jest myślowy model zegara wskazówkowego. Wielkości wejściowe są wprowadzane do obiektu za pomocą pokręteł umieszczonych z tyłu. Wielkościami wyjściowymi jest położenie wskazówek na cyferblacie. Cały mechanizm zegara przetwarza położenie pokręteł na położenie wskazówek. Zmiennymi stanu są sprężyny znajdujące się wewnątrz zegara. Zmienne stanu reprezentują zmagazynowaną w obiekcie energię. Kółka zębate są członami proporcjonalnymi i stanowią fizyczne połączenie pomiędzy wejściem, zmiennymi stanu i wyjściem. Można je interpretować jako współczynniki macierzy. Zmienne stanu są sterowalne, jeżeli kręcąc pokrętłami mamy wpływ na daną sprężynę. Zmienne stanu są obserwowalne, gdy stan danej sprężyny ma wpływ na położenie wskazówek. Sterowalność i obserwowalność zależy od wewnętrznych połączeń w strukturze obiektu. Dla obiektów liniowych wykryto [Kalman] odpowiedni warunek matematyczny, pozwalający testować wewnętrzną strukturę obiektu.

Twierdzenia o sterowalności i obserwowalności

Układ liniowy stacjonarny o jednym wejściu jest sterowalny wtedy i tylko wtedy, gdy rząd macierzy sterowalności Q jest pełny, gdzie

,

czyli rz Q = n.

W praktyce sprawdza się warunek : czy det Q ≠ 0.

Układ liniowy stacjonarny o jednym wyjściu jest obserwowalny wtedy i tylko wtedy, gdy rząd macierzy obserwowalności N jest pełny.

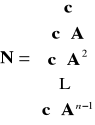
, czyli rz N = n.

W praktyce sprawdza się warunek det N ≠ 0.

Obiekt zapisany w postaci kanonicznej do sterowania jest w pełni sterowalny. Obiekt zapisany w postaci kanonicznej do obserwowania jest w pełni obserwowalny.

Liniowa transformacja wektora stanu.

Obiekt jest opisany przy pomocy następujących równań stanu :

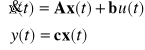
Chcemy by obiekt był opisany przy pomocy innego wektora stanu, zdefiniowanego w sposób następujący :

gdzie T - macierz transformacji, spełniająca następujące warunki :

dim T = n, co oznacza, że wektory x i v mają ten sam wymiar,

rz T = n ⇔ det T ≠ 0 - macierz jest nieosobliwa

W nowych współrzędnych obiekt jest opisany równaniami :

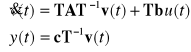
Transformacja T wektora stanu działa w sposób następujący na trójkę macierzy A, b, c.

Opis za pomocą wektora stanu nie jest jednoznaczny. Dwa obiekty mają taką samą dynamikę wtedy i tylko wtedy, gdy ich równania charakterystyczne maję te same pierwiastki. Liniowa transformacja wektora stanu nie zmienia położenia pierwiastków równania charakterystycznego.

Cele konstruowania układu regulacji automatycznej

0. Zapewnić stabilność

1. Spełnić wymogi, co do kształtu przebiegu przejściowego.

2. Spełnienie wymogów co do odchyłki statycznej.

3. Zapewnić sterowanie optymalne wg. określonego kryterium.

W punkcie 1. wymogi są określone za pomocą czasu regulacji, odchyłki dynamicznej, konieczności wyeliminowania zakłóceń.

Koncepcja realizacji celu.

Stosujemy proporcjonalne sprzężenie zwrotne od poszczególnych zmiennych stanu. Zakładamy, że wszystkie stany są dostępne pomiarowo.

x₁

z(t) x₂ y(t)

. . . . . . c

_ x_n

g₀

g₁

. . . ...

g_n

Po wprowadzeniu sprzężenia zwrotnego, nowe sterowanie ma postać :

, gdzie

.

Idąc tym tropem otrzymujemy (dla uproszczenia zapisu pomijamy w zapisie zależność od czasu):

Wprowadzenie sprzężenia zwrotnego doprowadziło do transformacji T trójki macierzy opisujących obiekt sterowania.

Sformułowanie zagadnienia

Dane:

1. Własności obiektu sterowania w postaci wektora współczynników wielomianu charakterystycznego :

2. Pożądane własności układu regulacji (obiekt z odpowiednim sprzężeniem zwrotnym) - również w postaci wektora współczynników wielomianu charakterystycznego :

Pożądany wielomian charakterystyczny dobieramy tak, aby były spełnione warunki 0 i 1. Uzyskujemy to przez odpowiednie umiejscowienie biegunów.

3. Macierze A, b są w postaci kanonicznej do sterowania.

Szukane :

Znaleźć taki wektor g , aby układ sterowania miał pożądane własności określone wektorem
.

Rozwiązanie :

Z jednej strony zachodzi :

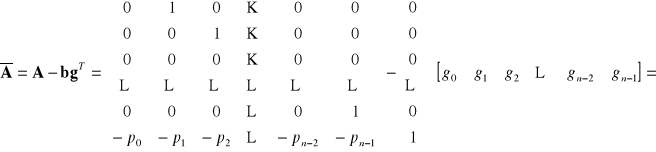
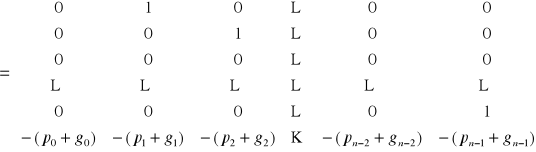
Z drugiej strony mamy :

,

zatem otrzymujemy układ równań :

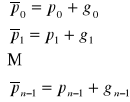
i ostatecznie

.

Wynik ten jest słuszny, jeżeli macierze A,b,c są w postaci kanonicznej dla sterowania. W przeciwnym przypadku musimy jeszcze dokonać odpowiedniej transformacji liniowej - o czym potem.

Obserwator stanu

Rozważania przeprowadzone wcześniej są słuszne, gdy wszystkie zmienne stanu są dostępne pomiarowo. Często zdarza się jednak tak, że poszczególne zmienne nie są dostępne dla układu regulacji. Wynika to z faktu , że nie jesteśmy w stanie w sposób zadowalający wyznaczać pochodnych wyższych rzędów ze zmierzonych sygnałów. Obserwatory stanu konstruuje się właśnie w celu udostępnienia zmiennych stanu.

Wydawałoby się, że nie ma tu żadnego problemu. Wystarczyłoby działać sygnałem wejściowym u(t) na układ o takich samych własnościach dynamicznych jak obiekt sterowania. Jednakże w praktyce nie znamy warunków początkowych, w jakich znajduje się obiekt. Jak również zakłócenia mogą powodować rozbieżność między rzeczywistymi zmiennymi stanu a ich estymatami generowanymi przez obserwator. Stąd też zachodzi konieczność konstruowania takiego obserwatora, dla którego ta rozbieżność dążyłaby asymptotycznie do zera.

Na początku lat 70-tych Luenberger zaproponował następującą strukturę obserwatora:

u(t)
c

x(t) y(t)

. . . . . . .

Naszym celem jest takie dobranie parametrów obserwatora (tzn. macierzy
) tak, aby :
, gdzie

Odejmując stronami równania dynamiki obiektu i obserwatora otrzymuje się :

Przyjmujemy, że macierze obserwatora są następujące :

czyli :

Otrzymaliśmy autonomiczny układ dynamiczny ze względu na e(t), którego rozwiązaniem jest (rozwiązanie jednorodnego układu równań różniczkowych) :

Jeżeli wartości własne macierzy
leżą w lewej półpłaszczyźnie, to spełniony jest warunek e(t) → 0. Wektor k dobieramy tak, by otrzymać jak najszybszą zbieżność.

-Sformułowanie zagadnienia

Dane :

1. wektor współczynników wielomianu charakterystycznego obiektu sterowania - p,

2. wektor współczynników wielomianu charakterystycznego obserwatora -
,

3. macierze A, c są w postaci kanonicznej dla obserwowania.

Szukane :

Tak dobrać wektor k, aby macierz
miała pożądane własności dynamiczne.

Rozwiązanie :

Z jednej strony mamy :

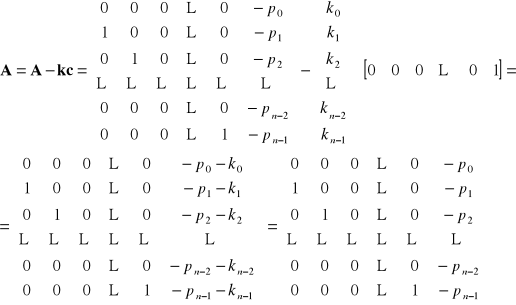
Prowadzi to do równości :

Dualność

Zagadnienia konstruowania regulatora i obserwatora są dualne. Podsumujmy uzyskane dotychczas rezultaty.

DANE :

Opis obiektu sterowania w przestrzeni stanów za pomocą macierzy A,b,c. Własności dynamiczne obiektu są określone przez współczynniki wielomianu charakterystycznego :

:

REGULATOR	OBSERWATOR
CEL
Tak dobrać wektor g , aby układ sterowanie miał pożądane własności dynamiczne :	Tak dobrać wektor k, tak aby obserwator miał pożądane własności dynamiczne :
TWIERDZENIE 1
1. Jeżeli obiekt jest w pełni sterowalny oraz 2. Macierze A, b są w postaci kanonicznej dla sterowania, TO :	1. Jeżeli obiekt jest w pełni obserwowalny oraz 2. Macierze A, c są w postaci kanonicznej dla obserwowania, TO :
TWIERDZENIE 2
Jeżeli obiekt jest w pełni sterowalny, ale macierze A, b są w dowolnej postaci TO :	Jeżeli obiekt jest w pełni obserwowalny, ale macierze A, c są w dowolnej postaci, TO :

Macierz W jest utworzona ze współczynników wielomianu charakterystycznego obiektu sterowania :

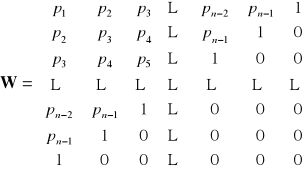
Algorytm konstruowania układu regulacji

1. Wyznacz współczynniki wielomianu charakterystycznego dla obiektu sterowania, pamiętając by p_n = 1.

2. Przedstaw obiekt w postaci kanonicznej dla obserwowania, sprawdź sterowalność (obserwowalność wynika z przyjętej postaci).

Jeżeli niedostępne są zmienne stanu to :

3. Określ pożądane własności dynamiczne obserwatora podając położenia biegunów :
.

4. Wyznacz współczynniki wielomianu charakterystycznego obserwatora, korzystając z zależności :

.

5. Wyznacz :
i przyjmij
,

6. Określ pożądane własności dynamiczne układu sterowania podając położenie biegunów :
.

7. Wyznacz współczynniki wielomianu charakterystycznego układu sterowania :

8. Wyznacz

---