Rafał Guzewicz
Gr. 27
Zespół 1
Ćwiczenie 35
Badanie pętli histerezy magnetycznej ferromagnetyków i ferrytów przy użyciu oscyloskopu.
1. Wiadomości wstępne.
Pojawienie się pętli histerezy na ekranie oscyloskopu jest wynikiem działania powszechnej siły tarcia, która występuje podczas przeorientowania domen w materiale. W wyniku działania zewnętrznego pola H wzrasta indukcja B w próbce (aż do wartości Bs -nasycenia) -krzywa pierwotnego namagnesowania. Przy zmniejszaniu pola zewnętrznego do 0, indukcja w próbce maleje osiągając wartość Br- indukcja szczątkowa- wykres jednak przechodzi inną drogą (krzywa II). Jeżeli przyłożymy teraz przeciwne pole H o wartości Hc zwanym polem koercji spowoduje zmalenie indukcji do zera. Przy dalszym wzroście pola natężenia H w tym kierunku indukcja będzie rosła osiągając nasycenie w kierunku przeciwnym (- BS). Idąc w drugą stronę otrzymujemy wykres symetryczny.
Przy dużym polu koercji o szerokiej pętli histerezy mówimy o ferromagnetyku twardym - wykorzystywanym m. in. do tworzenia magnesów trwałych. Gdy mamy małe pole koercji histerezy wąskiej pętli histerezy mówimy o ferromagnetyku miękkim - wykorzystywanym
m.in. do budowy rdzeni transformatorów.
Pole zawarte w pętli histerezy odpowiada pracy potrzebnej na przeorientowanie domen i jest miarą użyteczności materiału do konkretnych celów.
Podczas ćwiczenia zajmowaliśmy się badaniem pętli histerezy dla różnych materiałów.
W celu otrzymania pętli histerezy zastosowaliśmy oscyloskop. Schemat układu wykorzystanego w czasie ćwiczeń przedstawia poniższy rysunek:
Układ jest tak dobrany, aby wytwarzał sygnał napięciowy proporcjonalny do pola H (podawany jest on na płytki odchylające X) i sygnał napięciowy proporcjonalny do pola B (podawany na płytki odchylające Y).
2. Przebieg ćwiczenia
W pierwszym etapie ćwiczenia obserwowaliśmy obraz na ekranie oscyloskopu dla różnych materiałów. Pierwszym z nich musiał być ferromagnetyk miękki, ponieważ zaobserwowaliśmy na ekranie wąską pętlę histerezy. Dla drugiej próbki nie otrzymaliśmy żadnej pętli, więc był to paramagnetyk. Następne dwie próbki posiadały szeroką pętlę histerezy i wywnioskowaliśmy z tego, że są to materiały twarde.
W drugiej części ćwiczenia zbadaliśmy dwa toroidy, których parametry znajdują się w tabeli:
Materiał |
Pole przekroju
|
Liczba zwojów uzwojenia Pierwotnego |
Liczba zwojów uzwojenia wtórnego |
Długość uzwojenia
|
|
S+ΔS [m2] |
N1 |
N2 |
l+Δl [m] |
Ferryt (spiek) |
0,0001± 0,000002 |
130
|
1200 |
0,100±0,001 |
Permaloj (zwinięta taśma) |
0,000096 ±0,000004 |
250 |
600 |
0.080±0,001 |
Wyniki pomiarów znajdują się w tabelach poniżej.
Materiał: ferryt
Lp.:
|
I skuteczne w uzwojeniu pierwotnym
|
Wychylenie X na ekranie oscyloskopu dla:
|
Indukcji nasycenia
|
Indukcja resztkowa
|
|
|
|
Pola koercji
|
Maksymalnego wychylenia
|
|
|
|
Isk±∆Is [A]
|
xc ± ∆xc [mm]
|
xmax±∆xmax [mm]
|
US±∆US [V]
|
Ur+ΔUr [V] |
0,76 ± 0,11 |
25 ±1 |
31 ±1 |
0,095 ± 0,002 |
0,067 ± 0,002 |
|
0,66 ± 0,11 |
24 ±1 |
27 ±1 |
0,090 ± 0,002 |
0,063 ± 0,002 |
|
0,59 ± 0,11 |
45 ±1 |
49 ±1 |
0,085 ± 0,002 |
0,060 ± 0,002 |
|
0,54 ± 0,11 |
42 ±1 |
44 ±1 |
0,080 ± 0,002 |
0,056 ± 0,002 |
|
0,42 ± 0,11 |
33 ±1 |
34 ±1 |
0,074 ± 0,002 |
0,052 ± 0,002 |
|
0,33 ± 0,0367 |
27 ±1 |
0,060 ± 0,002 |
0,042 ± 0,002 |
||
0,27 ±0,0367 |
43 ±1 |
0,044 ± 0,002 |
0,031 ± 0,002 |
||
0,23 ± 0,0367 |
37 ±1 |
0,034 ± 0,002 |
0,024 ± 0,002 |
||
0,19 ± 0,0367 |
31 ±1 |
0,025 ± 0,002 |
0,018 ± 0,002 |
||
0,16 ± 0,0367 |
26 ±1 |
0,019 ± 0,002 |
0,013 ± 0,002 |
||
Błąd natężenia skutecznego (dla dwóch różnych zakresów):
![]()
![]()
![]()
Do obliczeń wartości B, H i μ skorzystaliśmy z następujących wzorów:
,
,
Nr
|
materiał |
Isk ± ΔIsk [A] |
Imax ± ΔImax [A] |
Uc ± ΔUc [V] |
H±ΔH [A/m] |
B ± ΔB [T] |
μ ± Δμ
|
1 |
FERRYT |
0,76 ± 0,11 |
1,075 ± 0,156 |
0,095 ± 0,002 |
1127 ± 216,2 |
0,158 ± 0,038 |
111,56 ± 48,23 |
2 |
|
0,66 ± 0,11 |
0,933 ± 0,156 |
0,090 ± 0,002 |
1078 ± 214,4 |
0,15 ± 0,036 |
110,73 ± 50,05 |
3 |
|
0,59 ± 0,11 |
0,834 ± 0,156 |
0,085 ± 0,002 |
995,7 ± 213,1 |
0,142 ± 0,034 |
113,49 ± 51,46 |
4 |
|
0,54 ± 0,11 |
0,764 ± 0,156 |
0,080 ± 0,002 |
948,1 ± 212,2 |
0,133 ± 0,033 |
111,63 ± 52,68 |
5 |
|
0,42 ± 0,11 |
0,594 ± 0,156 |
0,074 ± 0,002 |
749,5 ± 210 |
0,123 ± 0,03 |
130,68 ± 68,49 |
6 |
|
0,33 ± 0,0367 |
0,467 ± 0,052 |
0,060 ± 0,002 |
607,1 ± 73,5 |
0,1 ± 0,025 |
131,08 ± 48,64 |
7 |
|
0,27 ±0,0367 |
0,382 ± 0,052 |
0,044 ± 0,002 |
496,6 ± 72,4 |
0,073 ± 0,019 |
116,98 ± 47,58 |
8 |
|
0,23 ± 0,0367 |
0,325 ± 0,052 |
0,034 ± 0,002 |
422,5 ± 71,7 |
0,057 ± 0,016 |
107,49 ± 48,36 |
9 |
|
0,19 ± 0,0367 |
0,269 ± 0,052 |
0,025 ± 0,002 |
349,7 ± 71 |
0,042 ± 0,012 |
95,57 ± 46,79 |
10 |
|
0,16 ± 0,0367 |
0,226 ± 0,052 |
0,019 ± 0,002 |
293,8 ± 70,4 |
0,032 ± 0,01 |
86,67 ± 47,86 |
Do obliczenia Imax oraz ∆ Imax skorzystałem z następujących zależności:
Imax= Isk√2, ΔImax=Δ Isk√2
Do obliczenia błędu ∆H skorzystałem z metody różniczki zupełnej (wyniki wstawiłem
do tabeli):
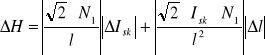
Do obliczenia błędu ∆B skorzystałem z metody różniczki zupełnej (wyniki wstawiłem do tabeli):
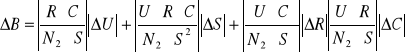
Jako ΔR i ΔC przyjęliśmy 10% wartości R i C.
Błąd ∆μ obliczyłem z metody różniczki zupełnej (wyniki wstawiłem do tabeli):
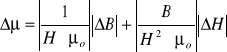
Materiał |
Bs ± ΔBs [T] |
Br ± ΔBr [T] |
FERRYT |
0,158 ± 0,038 |
0,112 ± 0,028 |
|
0,15 ± 0,036 |
0,105 ± 0,026 |
|
0,142 ± 0,034 |
0,1 ± 0,025 |
|
0,133 ± 0,033 |
0,093 ± 0,024 |
|
0,123 ± 0,03 |
0,087 ± 0,022 |
|
0,1 ± 0,025 |
0,07 ± 0,019 |
|
0,073 ± 0,019 |
0,052 ± 0,015 |
|
0,057 ± 0,016 |
0,04 ± 0,012 |
|
0,042 ± 0,012 |
0,03 ± 0,01 |
|
0,032 ± 0,01 |
0,022 ± 0,008 |
Tabela z wynikami dla drugiego toroidu:
Materiał permaloj
Lp.:
|
I skuteczne w uzwojeniu pierwotnym
|
Wychylenie X ekranie oscyloskopu dla:
|
Indukcji nasycenia
|
Indukcja Resztkowa
|
|
|
|
Pola koercji
|
Maksymalnego wychylenia
|
|
|
|
Isk±∆Is [A]
|
xc ± ∆xc [mm]
|
xmax±∆xmax [mm]
|
US±∆US [V]
|
Ur+ΔUr [V] |
1 |
0,005± |
23 |
38 |
0,040 |
0,034 |
2 |
0,0026± |
22 |
38 |
0,038 |
0,032 |
3 |
0,0013± |
38 |
0,036 |
0,03 |
|
4 |
0,00103± |
30 |
0,035 |
0,29 |
|
5 |
0,00083± |
25 |
0,034 |
0,28 |
|
6 |
0,00073± |
22 |
0,032 |
0,27 |
|
7 |
0,00063± |
46 |
0,03 |
0,25 |
|
8 |
0,00057± |
4 |
0,027 |
0,23 |
|
9 |
0,0005± |
36 |
0,025 |
0,02 |
|
10 |
0,00043± |
33 |
0,023 |
0,019 |
|
Nr
|
materiał |
Isk ± ΔIsk [A] |
Imax ± ΔImax [A] |
Uc ± ΔUc [V] |
H±ΔH [A/m] |
B ± ΔB [T] |
μ ± Δμ
|
1 |
PERMALOJ |
0,005± |
0,0071±0,0016 |
0,040 |
12,208± 0,228 |
0,139± 0,0362 |
9060,67±2528,91 |
2 |
|
0,0026± |
0,0037±0,0016 |
0,038 |
6,0856± 0,119 |
0,132±0,011 |
17259,65±1775,92 |
3 |
|
0,0013± |
0,0018±0,0016 |
0,036 |
5,114±0,059 |
0,125±0,011 |
19452,26±4081,39 |
4 |
|
0,00103± |
0,0015±0,0016 |
0,035 |
4,261±0,047 |
0,122±0,011 |
22784,44±2305,65 |
5 |
|
0,00083± |
0,0012±0,0016 |
0,034 |
3,409±0,038 |
0,118±0.011 |
27545,15±2874,81 |
6 |
|
0,00073± |
0,001±0,0016 |
0,032 |
2,841±0,033 |
0,111±0.01 |
31091,51±3162,18 |
7 |
|
0,00063± |
0,0009±0,0016 |
0,03 |
2,557±0,029 |
0,104±0.01 |
32366,28±3479,22 |
8 |
|
0,00057± |
0,0008±0,0016 |
0,027 |
2,273±0,026 |
0,094±0,01 |
32909,29±3877,43 |
9 |
|
0,0005± |
0,0007±0,0016 |
0,025 |
1,989±0,023 |
0,087±0,01 |
34807,64±4403,38 |
10 |
|
0,00043± |
0,0006±0,0016 |
0,023 |
1,705±0,02 |
0,08±0,009 |
37338,40±4638,56 |
![]()
![]()
Imax= Isk√2, ΔImax=Δ Isk√2
Do obliczenia błędów: ∆H, ∆B, ΔR, ΔC i ∆μ skorzystałem z zależności jak dla materiału pierwszego. Wszystkie wartości zostały od razu umieszczone w tabelach.
Materiał |
Bs ± ΔBs [T] |
Br ± ΔBr [T] |
Permaloj |
0,139±0,0362 |
0,118±0,011 |
|
0,132±0,011 |
0,111±0,011 |
|
0,125±0,011 |
0,104±0,01 |
|
0,122±0,011 |
0,101±0,01 |
|
0,118±0.011 |
0,097±0,01 |
|
0,111±0.01 |
0,094±0,01 |
|
0,104±0.01 |
0,087±0,01 |
|
0,094±0,01 |
0,08±0,01 |
|
0,087±0,01 |
0,069±0,009 |
|
0,08±0,009 |
0,066±0,009 |
Po zakończeniu części drugiej obserwowaliśmy co będzie się działo z pętlą histerezy ferromagnetyka stopniowo ogrzewanego. Po zanurzeniu materiału w oleju parafinowym i stopniowym podgrzewaniu widzieliśmy, że zachodzą zmiany na ekranie oscyloskopu. Pętla kurczyła się za sprawą spadku indukcji magnetycznej temperaturze.. Przy temperaturze około 250 oC stwierdziliśmy zanik pętli histerezy, czyli temperatura 250 oC dla badanego materiału jest temperaturą Curie. Stwierdzenie to jest jednak obarczone dużym błędem, ponieważ po odwróceniu procesu (wyjęliśmy próbkę z oleju i czekaliśmy, aż ostygnie) pętla histerezy pojawiła się dopiero dla temperatury 140 oC.
Wnioski
Zakładając, że wykonane obliczanie są wystarczające do porównania obu materiałów, można powiedzieć, że oba przedstawione tu materiały różnią się właściwościami magnetycznymi. Ich współczynniki przenikalności magnetycznej różnią się aż o kilka rzędów. Potwierdzają to też różne obrazy ich pętli histerezy zaobserwowane na oscyloskopie. Trudno wyciągnąć jakieś głębsze wnioski z wykonanych na podstawie pomiarów obliczeń, ponieważ uzyskaliśmy stosunkowo wysokie wartości błędów (sięgające w niektórych przypadkach nawet 50%), przez co możemy je traktować tylko orientacyjnie.
Wyszukiwarka