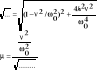
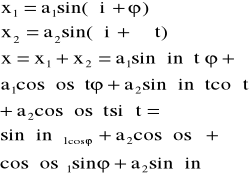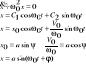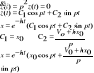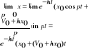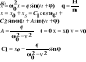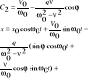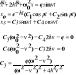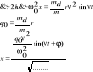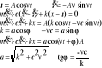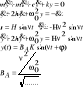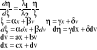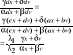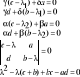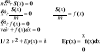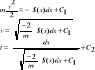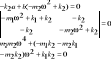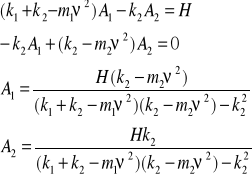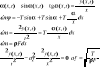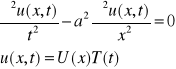Składanie ruchów harmonicznych: a) ta sama częstość. Wykonajmy podstawienie:

gdzie:

Suma ruchów n-harmonicznych:

b) dwa przebiegi harmoniczne o różnych częstościach drgań własnych i różnych przesunięciach fazowych: Możemy wyróżnić trzy przypadki: 1. a1<a2 i ω1<<ω2. Drgania wypadkowe:

2. a1>a2 i ω1<<ω2

3. ω1 i ω2 różnią się o niewielki przyrost Δω: Oznaczmy:

gdzie:

Taki przebieg drgań nazywamy dudnieniem:

c) stosunek częstości dwóch przebiegów harmonicznych jest pewną liczbą naturalną: ϕ=0

ϕ=π/2

Analiza harmoniczna: Każdy przebieg okresowy możemy rozłożyć na szereg składowych harmonicznych. Analiza opiera się na przedstawieniu dowolnego przebiegu okresowego za pomocą szeregu Fouriera:

Składowa dla n=1 nazywa się składową podstawową. Aby scharakteryzować amplitudy poszczególnych harmonicznych w widmie częstości tworzymy pary licz zapisanych w postaci:

Układanie równań ruchu: a) metoda oparta na prawie zachowania energii (metoda Rayleigha). Można ją stosować tylko do układów autonomicznych, w których mamy do czynienia ze stałością energii: b) metoda Newtona:

c) metoda d'Alemberta: d) równanie Lagrange'a II rodzaju: Qj - uogólniona siła zewnętrzna Rj - uogólniona siła tłumienia

Siły w ruchu drgającym: Siły zależne od przemieszczenia x nazywają się siłami wznawiającymi lub restytucyjnymi. Rodzaje sił wznawiających: a) siły grawitacyjne:

b) siły sprężyste:

Siły zależne od prędkości nazywamy siłami oporu. Są one zwykle skierowane przeciwnie do ruchu ciała. Rozpraszają energię powodując zanikanie ruchu. Niekiedy są skierowane zgodnie z ruchem ciała i wtedy mówimy o tzw. drganiach samowzbudnych. Najczęściej w układach liniowych mamy tłumienia wiskotyczne: . Siły zależne od czasu nazywamy siłami

wymuszającymi. Rodzaje: a) siły harmoniczne o stałej amplitudzie: b) wymuszenie bezwładnościowe:

c) wymuszenie kinematyczne:

d) wymuszenie impulsowe.

Klasyfikacja drgań: 1. Drgania układów o 1 st swobody, 2. O wielu st swobody, 3. Drgania układów ciągłych (o nieskończenie wielkiej liczbie stopni swobody). 1. drgania swobodne (brak siły wymuszającej), 2. Drgania samowzbudne. 3. Drgania wymuszone. 1. Nietłumione, 2. Tłumione. Oraz drgania parametryczne - parametry układu zmieniają się okresowo w czasie (np. sztywność), drgania liniowe i nieliniowe.

Drgania liniowe o 1^st swobody: Gdzie:

Energia takiego układu: Po podstawieniu x' i x i , że ω0^2=k/m i uproszeczeniu otrzymujemy:

Drgania swobodne o 1^st swobody z tłumieniem: Podstawiamy x", x' i x, oraz: otrzymujemy:

1. przypadek: h<ω0 p>0 tłumienie podkrytyczne: podst.

2. h=ω0=hkr Drgania krytyczne p=0

3. Drgania nadktytyczne h>ω0

Logarytmiczny dekrement tłumienia: wyraża sobą miarę tłumienia w układzie:

Drgania wymuszone:

1 część obrazuje drgania własne z częstością ω0 zależne tylko od warunków początkowych. Część 2 opisuje drgania własne zależne od siły wymuszające. Część 3 obrazuje drgania wymuszone. Aby uniknąć drgań 1 i 2 stałe C1 i C2 muszą być jednocześnie równe 0. Prowadzi to do następujących war. Pocz.

Dla ϕ=0 Dla ϕ=π/2

Współczynnik uwielokrotnienia amplitudy - stosunek amplitudy siły wymuszającej działającej w sposób statyczny do ugięcia statycznego (λst=q/ω0^2). Dla 2 przypadku: dla ϕ=0:

Dla przypadku 3:

Drgania wymuszone z tłumieniem:

Wymuszenie bezwładnościowe:

Wymuszenie kinematyczne:

Amortyzacja drgań: zniwelowanie skutków oddziaływania drgań. 1. przypadek - ochrona otoczenia od drgań układu:

ε - współczynnik prze-noszenia. Jeżeli ν/ω0> wtedy wsp-ółczynnik przenoszenia <1. Należy tak dobrać sztywność k, aby był spełniony warunek:

b) ochrona układu od drgań pochodzą-cych z otoczenia: W tym przypadku chcemy ochronić maszynę przed oddziaływaniem środowiska. Warunki optymalizacji zostają dokładnie takie same jak w przypadku a). Zależności na przebieg współczynnika amortyzacji są identyczne.

Doświadczalne określenie amplitud i przyspieszeń: Doświadczalny pomiar pozwala określić zakresy niebezpiecznych częstości, dużych amplitud w ruchu drgającym. Gdy drgania wykorzystywane są w sposób pasożytniczy pomiar pozwala określić optymalne zakresy prac urządzenia. a) pomiar parametrów, gdy badamy drgania względem nieruchomego układu rejestrującego:

b) badanie drgań względnych obiektu drgającego i czujnika drgań: Masa przemieszcza się o x, obiekt drgający o s. Przemieszczenie względne y=x-s.

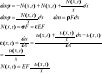
Widać z przebiegu Ba, że przyrząd sejsmiczny do pomiaru przemieszczeń powinien mieć częstość drgań własnych znacznie mniejszą od częstości drgań mierzonych. Jeżeli rozwiązanie tego równania przedstawimy w postaci:

Przyrządy sejsmiczne do pomiaru przyspieszeń powinny być tak skonstruowane, aby ich częstość własna była wielokrotnie wyższa od częstości drgań mierzonych.

Badania drgań na płaszczyźnie (przestrzeni) fazowej: badania topolo-giczne - na płaszczyźnie prędkość w fun-kcji przemieszczenia. Aby otrzymać ró-wnanie w formie potrzebnej do badania rozwiązania na płaszczyźnie fazowej sprowadzamy go do równania I stopnia. Trajektoria fazowa - miejsce geometry-czne wszystkich punktów odwzorowu-jących krzywą całkową równania Gdy trajektoria fazowa

jest linią zamkniętą - cykl graniczny. Styczna do trajektorii fazowej tworzy pewien kąt którego Jeśli jest on określony to mówimy o punktach regularnych (zwykłych). Jeżeli tg jest nieokreślony mówimy o punktach osobliwych.

Ogólne równanie ruchu: Gdy P i Q rozwiniemy w szereg potęgowy to cha-rakter punktów osobliwych można okre-ślić na podstawie części liniowej tych

funkcji: (dla układów liniowych). Przyjmijmy:

Po rozwinięciu i porównaniu wyrażenia z x i v w liczniku i mianowniku:

Każdej wartości c odpowiada jedna trajektoria fazowa. Jej charakter zależy od lambd. a) λ1≠λ2 - rzeczywiste, jednakowe znaki , gdy punkt osobliwy nosi nazwę węzła. B+c<0 węzeł stateczny. B+c>0 niestateczny.

B) λ1≠λ2 - rzeczywiste, mają przeciwne znaki, gdy (b-c)^2 +4ad>0 i bc-ad<0. Punkt osobliwy - siodło (niestateczne).

c) λ1 λ2 - zespolone, ale żadna z nich nie jest ani czysto rzeczywista, ani czysto urojona. (b-c)^2 +4ad<0 i b+c≠0. Otrzymujemy ognisko. B+c<0 stateczne, b+c >0 niestateczne.

d) sprzężone, czysto urojone: (b-c)^2 +4ad<0 i b+c=0. Środek lub centrum. Trajektorie fazowe są krzywymi zamkniętymi okrążającymi punkt osobliwy.

Zachowanie energii w drganiach liniowych: Każda trajektoria fazowa jest krzywą stałej energii mechanicznej. Minima-

lnej wartości energii potencjalnej odpo-wiada stateczne położenie równowagi. Pewnej wartości Ep=C1 odpowiada określona amplituda drgań a1. Dla układów nieliniowych:

Ep - energia potencjalna odniesiona do jednostki masy, h - energia mechaniczna układu. Zależność ta opisuje równanie trajektorii fazowej. Punkty, w których energia potencjalna ma wartości ekstremalne są punktami osobliwymi. W punktach tych

Jeżeli ekstremum energii potencjalnej to minimum, punkt osobliwy jest środkiem (centrum). Jeżeli maksimum to punkt osobliwy siodło (niestateczne).

Drgania nieliniowe: nie jest prawdziwa zasada superpozycji (złożenie wypadko-wego przebiegu z kilku przebiegów po-wstałych pod działaniem np. sił wymu-szających nie jest przebiegiem rzeczy-wistym w rozpatrywanym układzie). Rozwiązanie zależy bardzo silnie od warunków początkowych. Przy jednej danej częstości siły wymuszającej może wystąpić kilka rezonansów, mogą wystąpić drgania będące ułamkiem częstości siły wymuszającej, a także

drgania o częstościach będących krotnością częstości siły wymuszającej. Mimo nie istniejącego tłumienia mogą się pojawić drgania o skończonej wartości - drgania samowzbudne. Metoda ścisła Ek+Ep=const: S(x) - nieliniowa siła sprężysta:

Charakter S(x) pozwala na dokładne

rozwiązanie przez całkowanie za pomocą funkcji eliptycznych lub metodami numerycznymi. Metoda małego parametru (swobodne)

Metoda mał. Parametru (wymuszone)

Przykładowy przebieg krzywej rezonansowej dla drgań nieliniowych wymuszonych: Przy 1 stosunku ni/omega możliwe są drgania o 1 amplitudzie, przy drugim o dwóch, przy trzecim o trzech. To jakie drgania powstaną zależne jest od warunków początkowych przed włączeniem siły wymuszającej. Gdy stan układu jest w położeniu A to siła wymuszająca wywoła drgania o amplitudzie B1. Gdy był w stanie C to amplituda wzrośnie do B1.

Gdy był w D lub E to amp B3. Drgania B1 i B3 są stateczne. Drgania B2 można wywołać tylko przez specjalny dobór war pocz. Dla drgań tłumionych:

Zjawisko zeskoku: Jeżeli w badaniach układu nieliniowego doświadczalnie odtworzymy krzywą rezonansową zmie-niając częstości wymuszenia to kolejne stany drganiowe ustalą się kolejno przez punkty ABCDE. Przy dalszym zwiększaniu częstości nastąpi przeskok do punktu F i związana z tym zmiana amplitudy. Dalej amplituda zmieniać się będzie po krzywej FG. Gdy będziemy zmieniać częstości wymuszenia od większych (G) to w H nastąpi przeskok

do I i dalej amplituda zmieniać się będzie wzdłuż ICBA. Odcinek HE jest praktycznie nie do zrealizowania ze względu na niestateczność tych drgań.

Drgania swobodne o 2 st swobody:

Różniczkujemy i podstawiamy do równań. Równania te muszą być spełnione dla całego zakresu czasu t więc:

Układ o 2 st swobody ma dwie częstości drgań własnych. Jeżeli stosunek amplitud a/b>0 to masy drgają współbieżnie.

Jeżeli a/b<0 to masy drgają przeciwbieżnie.

Drgania wymuszone o 2 st swobody:

Rozwiązanie szczególne: różniczkujemy i podstawiamy do układu równań. Otrzymujemy:

Wprowadzamy współczynnik uwielokrotnienia amplitudy:

W przypadku gdy ν=ω1=ω2 wtedy μ1=0. Całkowity zanik drgań ciała o masie m1. Jest to tłumienie dynamiczne. Tłumik wykonuje następujący ruch:

Reakcja sprężyny jest równa co do wartości sile wymuszającej i ma zwrot przeciwny. Wady: drgania ciała 1 tłumione są do 0, praktycznie tylko dla jednej częstości siły wymuszającej. Tłumik jest mało efektywny. Po wprowadzeniu elementu tłumiącego między ciałami to równania ruchu:

Następuje wyraźne złagodzenie rezonansu. Nie następuje tłumienie do zera. Można tak dobrać punktu P i Q aby styczne do krzywych rezonansowych

w tych punktach były poziome. Występuje wtedy najsilniejsze złagodzenie rezonansu w szerokim zakresie częstości siły wymuszającej. Tłumik dynamiczny można nastroić na dwa sposoby: a) przy sile wymuszającej o stałej częstości stosuje się małe tłumienie, które eliminuje rezonans główny i prowadzi do warunku ν=ω1=ω2 spełnionego w przybliżeniu. B) wartość siły wymuszającej zmienia się w pewnym zakresie lub istnieje możliwość

występowania sił wymuszających o różnych częstościach stosujemy tłumik o większym współczynniku tłumienia i dobieramy parametry tak, aby uzyskać obniżenie amplitudy drgań ciała głównego w szerokim zakresie częstości.

Drgania układów ciągłych: a) równanie drgań struny: zakładamy: poprzeczne wymiary są znikomo małe, może wykonywać ruchy poprzeczne.

b) równanie drgań podłużnych pręta: pręt jednorodny, o stałym przekroju. Przekroje pozostają płaskie.

Problem brzegowy:

Spełnienie tej zależności dla każdego t i x jest możliwe tylko wtedy, gdy obie strony równania będą stale równe stałej wielkości:

War brzeg. u(0,t)=0 oraz warunki początkowe: u(x,0)=u0(x) oraz Podst. To do u(x,t)=U(x)T(t) mamy: U(0,t)=U(0)T(t)=0 oraz

T(t) nie może być =0. Ostatecznie otrzymujemy warunki brzegowe na funkcję U w postaci: U(0)=0 oraz U'(l)=0. Funkcje, które spełniają te warunki nazywamy funkcjami własnymi. Wartości ω dla których istnieją funkcje własne nazywamy wartościami własnymi.

Rozwiązanie na U(x): po podstawieniu war brzeg, oraz nietrywialne rozwiązanie jest możliwe, gdy:

Gdy ω=0 to U(x)=0. Gdy ω≠0 to Otrzymujemy nieskończony ciąg wartości własnych, każdej z nich odpowiada funkcja własna:

Musi ona spełniać warunki brzegowe oraz uwzględniając mamy Bn=0 czyli

---