Sprawozdanie nr 5
Ćwiczenie składało się z dwóch części.
Pierwsza część:
Pomiar wielkości æ = cp/cv.
W tym celu dokonaliśmy 10 pomiarów ciśnienia. Układ pomiarowy składał się ze szklanego balonu połączonego z pompką, manometrem oraz zaworkiem do kontroli ciśnienia we wnętrzu balonu.
Najpierw podwyższaliśmy ciśnienie powyżej ciśnienia atmosferycznego, następnie czekaliśmy do ustalenia się ciśnienia i zapisywaliśmy wartość h1, następnie otwieraliśmy zawór na krótki czas, aby ciśnienie zrównało się z atmosferycznym. Następnie przed dokonaniem kolejnego pomiaru czekaliśmy na kolejne ustalenie się ciśnienia i zapisywaliśmy pomiar jako h2.
Oto dokonane pomiary:
h'(mm) |
h”(mm) |
(h”-h')= h1 |
h'(mm) |
h”(mm) |
(h”-h')=h2 |
h1/(h1-h2)=æ |
155 |
449 |
294 |
270 |
332 |
62 |
1,27 |
160 |
442 |
282 |
269 |
335 |
66 |
1,31 |
154 |
450 |
296 |
270 |
334 |
64 |
1,28 |
178 |
425 |
247 |
272 |
331 |
61 |
1,33 |
240 |
365 |
125 |
288 |
315 |
27 |
1,28 |
225 |
380 |
108 |
285 |
320 |
35 |
1,48 |
272 |
332 |
60 |
296 |
308 |
12 |
1,25 |
132 |
470 |
338 |
263 |
340 |
77 |
1,30 |
150 |
453 |
303 |
271 |
333 |
62 |
1,26 |
215 |
390 |
175 |
281 |
322 |
41 |
1,31 |
Błędy systematyczne:
∆h=+-4mm
spowodowane :
+-2mm - menisk w manometrze
+- 1mm niepewność miarki w manometrze
+- 1mm paralaksa
-Średnia wartość æ=(1,27+1,31+1,28+1,33+1,28+1,48+1,25+1,30+1,26+1,31)/10=1,31
-błąd przypadkowy æ :
σ = |x - x|
σ1 =|1,27 - 1,30| = 0,03
σ2= |1,31 - 1,30| = 0,01
σ3= |1,28 - 1,30| = 0,02
σ4 =|1,33 - 1,30| = 0,03
σ5 =|1,28 - 1,30| = 0,02
σ6 =|1,48 - 1,30| = 0,18
σ7 =|1,25 - 1,30| = 0,05
σ8 =|1,30 - 1,30| = 0
σ9 =|1,26 - 1,30| = 0,04
σ10=|1,31 - 1,30| = 0,01
-średni błąd kwadratowy:
Sx= 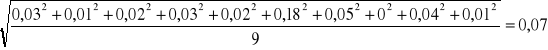
-błąd wartości średniej:
![]()
Zatem Wyliczona przez nas wartość æ = 1,31 +- 0,02
Wykres zależności h1(h2):
Współczynnik nachylenia prostej wynosi b= 0,207 +- 0,017
Wnioski:
Wyliczona wartość æ różni się znacząco od wartości teoretycznej, która w przypadku powietrza wynosi 1,4. Spowodowane jest to wieloma czynnikami, do teoretyczne æ wyznaczane było dla gazu doskonałego, którym to powietrze nie jest, następnie brak precyzyjnych przyrządów pomiarowych. Posiadane przyrządy miały duży błąd, a odczytywanie wyników było mocno subiektywne i inne dla każdego, kto odczytywał wynik. Czynnik ludzki oddziaływał tu w bardzo dużym stopniu.
Co widać w różnicy błędów systematycznych i przypadkowych.
Część druga
Wyznaczanie ciepła parowania wody na podstawie zależności temp. wrzenia od ciśnienia.
W tym ćwiczeniu mierzyliśmy temperaturę wrzenia wody w zależności od ciśnienia jakie panuje w bańce z wodą.
Do tego celu posłużył nam układ, którego schemat przedstawiam poniżej.
Przed wykonaniem pomiarów sprawdziliśmy ciśnienie atmosferyczne, jakie panuje w otoczeniu i wynosiło ono 990hPa czyli 742,56mmHg.
Oto wyniki naszych pomiarów:
Nr pomiaru |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
T[K] |
313,5 |
331,5 |
338,4 |
349,6 |
353 |
358 |
363 |
366 |
368 |
373 |
P mmHg(h1+h2) |
690 |
620 |
540 |
420 |
344 |
200 |
180 |
100 |
60 |
0 |
Następnie przeliczam ciśnienia na hPa za pomoca wzoru p = p0-(h1+h2)*ρg
p0 - ciśnienie atmosferyczne w danym momencie
h1-h2 - odchylenia poziomów rtęci w manometrze
g = 9.81 N/kg
ρ = 13.6 g/mm
Wyniki w tabelce poniżej:
Nr pomiaru |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Ciśnienie p(hPa) |
69,43 |
162,82 |
269,55 |
429,65 |
531,05 |
723,17 |
749,85 |
856,58 |
909,95 |
990 |
Poniżej wykres zależności temperatury od ciśnienia.
Następnym krokiem były obliczenia do wykonania kolejnego wykresu.
Wykresu lnp(1/T-1/T0)
*lnp:
ln(690)= 6,54
ln(620)=6,43
ln(540)=6,29
ln(420)=6,04
ln(344)=5,84
ln(200)=5,30
ln(180)=5,19
ln(100)=4,60
ln(60)=4,09
*(1/T-1T0)
1/313 K - 1/373 K= 0,00051K
1/331,5 K - 1/373 K= 0,00033 K
1/338,4 K - 1/373 K= 0,00027 K
1/349,6 K - 1/373 K=0,00017
1/353 K - 1/373 K= 0,00015
1/358 K - 1/373 K=0,00011
1/363 K - 1/373 K=0,00007
1/366 K - 1/373 K=0,00005
1/368 K - 1/373 K=0,00004
Wyniki Przedstawia tabelka:
lnp |
6,54 |
6,43 |
6,29 |
6,04 |
5,84 |
5,30 |
5,19 |
4,60 |
4,09 |
ln 0 |
1/T - 1/T0[K] |
0,00051 |
0,00033 |
0,00027 |
0,00017 |
0,00015 |
0,00011 |
0,00007 |
0,00005 |
0,00004 |
0 |
Współczynnik nachylenia prostej wynosi B = 4622,15 +- 1123,48
Na podstawie wykresu możemy wyznaczyć molowe ciepło parowania L , a następnie z tego ciepło parowania Lp.
lnp - lnp0 = (L/R)*(-1/T+1/T0)
lnp = (lnp0 +L/RT0)-L/RT
a= L/R
b=Lnp0 -1/RT0
a= 4622,15 +-1123,48
R=8,31 J/mol
L=R*a => 8,31 J/mol *4622,15= 38410,07 J/mol
∆L=∆a *R= 1123,48 *8,31 J/mol = 93336,12 J/mol
Lp= L/µ
µ=18g/mol
Lp= 38410,07J/mol / 18 g/mol =2133,89 J/g
∆Lp= 93336,12J/mol / 18 g/mol = 118,55 J/g
Lp eksperymentalne 2133,89 J/g +- 118,55 J/g (p=990 hPa)
Lp tablicowe 2300J/g (p=1013hPa)
Wnioski:
Wyznaczona wartość ciepła parowania różni się nieznacznie od tablicowej wartości. Jednak różnica ta jest dużo mniejsza niż przy pomiarze wartości æ w poprzedniej części ćwiczenia. Odchylenie te mieści się w granicy błędu. Wynika to z tego, że układ pomiarowy jest tu dużo bardziej zaawansowany i skomplikowany przez to dokładniejszy.
Ta niewielka różnica wynika z tego, iż pomiar książkowy dokonany był przy ciśnieniu 1013 hPa. A pomiar wykonywany w tym ćwiczeniu w ciśnieniu atmosferycznym 990 hPa.
Wyszukiwarka