Waldemar Gancarz
I BD 6.03.2009
Laboratorium z fizyki
Ćw. nr 27
Wyznaczanie indukcyjności cewki i pojemności kondensatora
w obwodzie prądu zmiennego
I. Zagadnienia do samodzielnego opracowania
Prąd sinusoidalnie zmienny, wielkości charakterystyczne - wartość średnia, skuteczna i szczytowa.
Prąd sinusoidalnie zmienny jest to charakterystyczny przypadek prądu elektrycznego okresowo zmiennego, w którym wartości chwilowe podlegają zmianom w powtarzalny, okresowy sposób, z określoną częstotliwością. Prąd sinusoidalny - zależności: natężenia prądu sinusoidalnego od czasu,
a także napięcia od czasu są opisane za pomocą matematycznej funkcji sinus:
I = I0sinωt oraz U = U0sinωt
gdzie: I0 - wartość maksymalna (szczytowa) natężenia albo inaczej amplituda natężenia, U0 - wartość maksymalna (szczytowa) napięcia albo inaczej amplituda napięcia, ω - tzw. częstość kołowa prądu przemiennego; jest to wielkość równa prędkości kątowej, z jaką obraca się wirnik prądnicy wytwarzającej dany prąd przemienny.
Wartość średnia (natężenia, napięcia, itd.) prądu okresowego to wartość takiego umyślonego
prądu stałego, który w czasie jednego okresu przenosi taki sam ładunek jak dany prąd okresowy.
Iśr=0
Wartość skuteczna (natężenia, napięcia, itd.) to wartość odpowiedniego parametru (natężenia, napięcia, itd.) takiego, umyślonego prądu stałego, który daje identyczny skutek energetyczny jak dany prąd okresowy (w tym samym czasie, będącym wielokrotnością jednego okresu).
Najczęściej definicję tę odnosi się do prądu przepływającego przez rezystor: wartość
skuteczna prądu okresowego to taka wartość umyślonego prądu stałego, który przepływając przez niezmienną rezystancję R w czasie jednego okresu T, powoduje wydzielenie na tej rezystancji takiej samej ilości energii cieplnej, co prąd okresowy w tym samym czasie.
![]()
Elementy R, L, C w obwodzie prądu zmiennego. Pojęcie reaktancji.
Reaktancja lub opór bierny to wielkość charakteryzująca obwód elektryczny zawierający kondensator (pojemność) lub cewkę (indukcyjność). Jednostką reaktancji jest Ohm. Reaktancję oznacza się na ogół symbolem X.
Reaktancja cewki (opór indukcyjny, induktancja) ma znak dodatni i oblicza się ją ze wzoru:
gdzie L to indukcyjność własna cewki,
pulsacja.
Reaktancja kondensatora (opór pojemnościowy, kapacytacja) oblicza się ją ze wzoru:
gdzie: C - pojemność kondensatora,
- pulsacja.
We wzorze na reaktancję składowa indukcyjna występuje ze znakiem dodatnim, a pojemnościowa - z ujemnym:
Wykresy wektorowe (fazowe).
Obwód szeregowy R L C. Pojęcie impedancji.
Impedancja, moduł impedancji, opór całkowity (ozn. Z) - wielkość opisująca elementy w obwodach prądu przemiennego.
Impedancja jest rozszerzeniem pojęcia rezystancja z obwodów elektrycznych prądu stałego, umożliwia rozszerzenie prawa Ohma na obwody prądu przemiennego.
Impedancja Z elementu obwodu prądu przemiennego jest definiowana jako
gdzie:
Ur - napięcie elektryczne,
Ir - natężenie prądu przemiennego.
Jest wypadkową oporu czynnego (rezystancji) R i biernego (reaktancji) X.
II. Metodologia wykonania ćwiczenia.
Układy pomiarowe do wyznaczania indukcyjności cewki i pojemności kondensatora
przy wykorzystaniu prawa Ohma tzw. metodą techniczną przedstawione są na rysunkach poniżej.
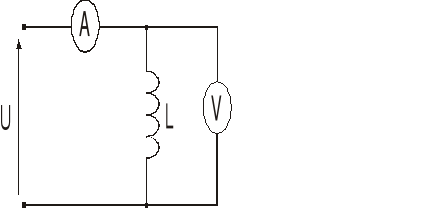
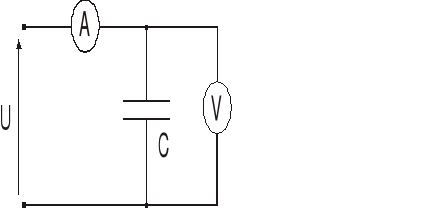
1. Zmontować obwód pomiarowy dla cewki do pomiarów przy prądzie stałym. Przy łączeniu obwodu zwrócić uwagę, aby zastosować mierniki przeznaczone dla prądu stałego.
2. Zasilając obwód pomiarowy dla cewki prądem stałym odczytać wartości prądu dla różnych wartości napięcia (max 12V).
3. Zmontować obwód pomiarowy dla cewki do pomiarów przy prądzie przemiennym.
Przy łączeniu obwodu zwrócić uwagę, aby zastosować mierniki przeznaczone dla prądu przemiennego. Mierniki prądu stałego zasilone prądem przemiennym ulegną uszkodzeniu!
4. Zasilając obwód pomiarowy prądem przemiennym odczytać wartości prądu dla różnych wartości napięcia (![]()
).
5. Pomiarów dla kondensatora przy prądzie stałym nie wykonuje się.
6. Zmontować obwód pomiarowy dla kondensatora do pomiarów przy prądzie przemiennym. Przy łączeniu obwodu zwrócić uwagę, aby zastosować mierniki przeznaczone dla prądu przemiennego. Mierniki prądu stałego zasilone prądem przemiennym ulegną uszkodzeniu!
7.Zasilając obwód dla kondensatora prądem przemiennym odczytać wartości prądu dla różnych wartości napięcia (![]()
).
Zależność U(I) dla obwodu z cewką prąd stały.
U_[ V] |
I_[A] |
u(U_)[V] |
u(I_)[A] |
R[Ω] |
Ru(R) [Ω] |
||
1 |
0,065 |
|
|
16,8 |
16,8±0,1 |
|
|
2 |
0,125 |
|
|
|
|
|
|
3 |
0,18 |
|
|
|
|
|
|
4 |
0,245 |
|
|
|
|
|
|
5 |
0,310 |
|
|
|
|
|
|
6 |
0,36 |
|
|
|
|
|
|
7 |
0,42 |
|
|
|
|
|
|
8 |
0,485 |
|
|
|
|
|
|
9 |
0,535 |
|
|
|
|
|
|
10 |
0,59 |
|
|
|
|
|
|
11 |
0,65 |
|
|
|
|
|
|
12 |
0,71 |
|
|
|
|
|
|
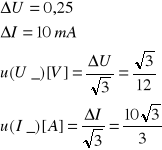
Wykres zależności U(I) cewki dla prądu stałego:
Zależność U(I) dla obwodu z cewką prąd zmienny.
|
|
u(U~)[V] |
u(I~)[A] |
Z[Ω] |
Zu(Z) [Ω] |
Lu(L) [Ωs] |
10 |
0,20 |
|
|
62,7 |
63,5±0,2 |
|
20 |
0,34 |
|
|
|
|
|
30 |
0,52 |
|
|
|
|
|
40 |
0,70 |
|
|
|
|
|
50 |
0,86 |
|
|
|
|
|
60 |
1,08 |
|
|
|
|
|
70 |
1,20 |
|
|
|
|
|
70 |
1,38 |
|
|
|
|
|
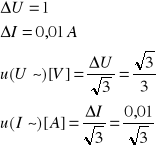
Wykres zależności U (I) cewki dla prądu zmiennego:
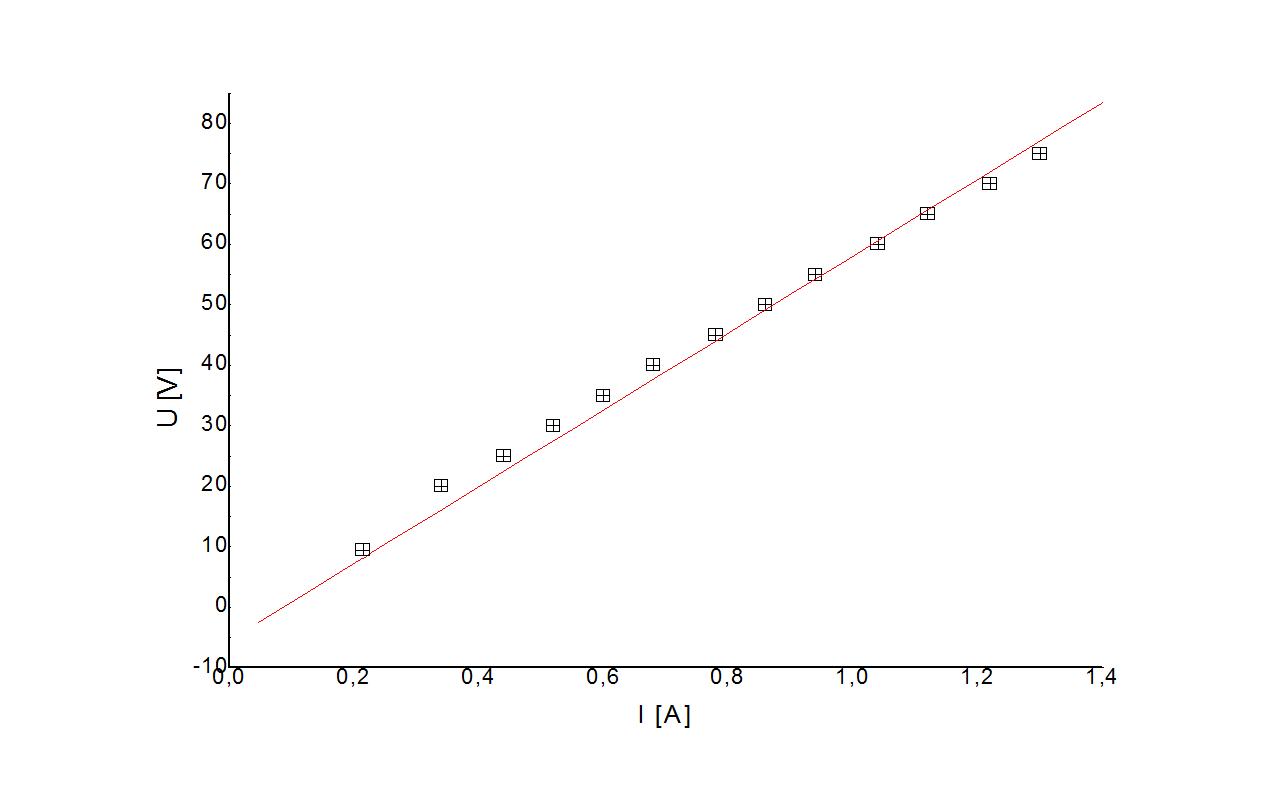
Obliczam indukcyjność cewki przyjmując za ƒ=50Hz:
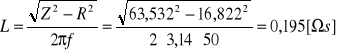
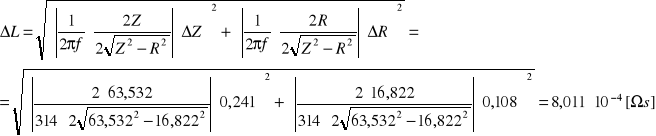
Zależność U(I) kondensatora dla prądu zmiennego.
|
|
u(U~)[V] |
u(I~)[A] |
XC [Ω] |
XCu(XC) [Ω] |
Cu(C) [µF] |
10 |
0,1 |
|
|
100 |
100±0,3 |
32,1±0,1 |
20 |
0,2 |
|
|
|
|
|
30 |
0,3 |
|
|
|
|
|
40 |
0,4 |
|
|
|
|
|
50 |
0,51 |
|
|
|
|
|
60 |
0,6 |
|
|
|
|
|
70 |
0,71 |
|
|
|
|
|
80 |
0,8 |
|
|
|
|
|
90 |
0,91 |
|
|
|
|
|
100 |
1 |
|
|
|
|
|
Wykres zależności U (I) kondensatora dla prądu zmiennego
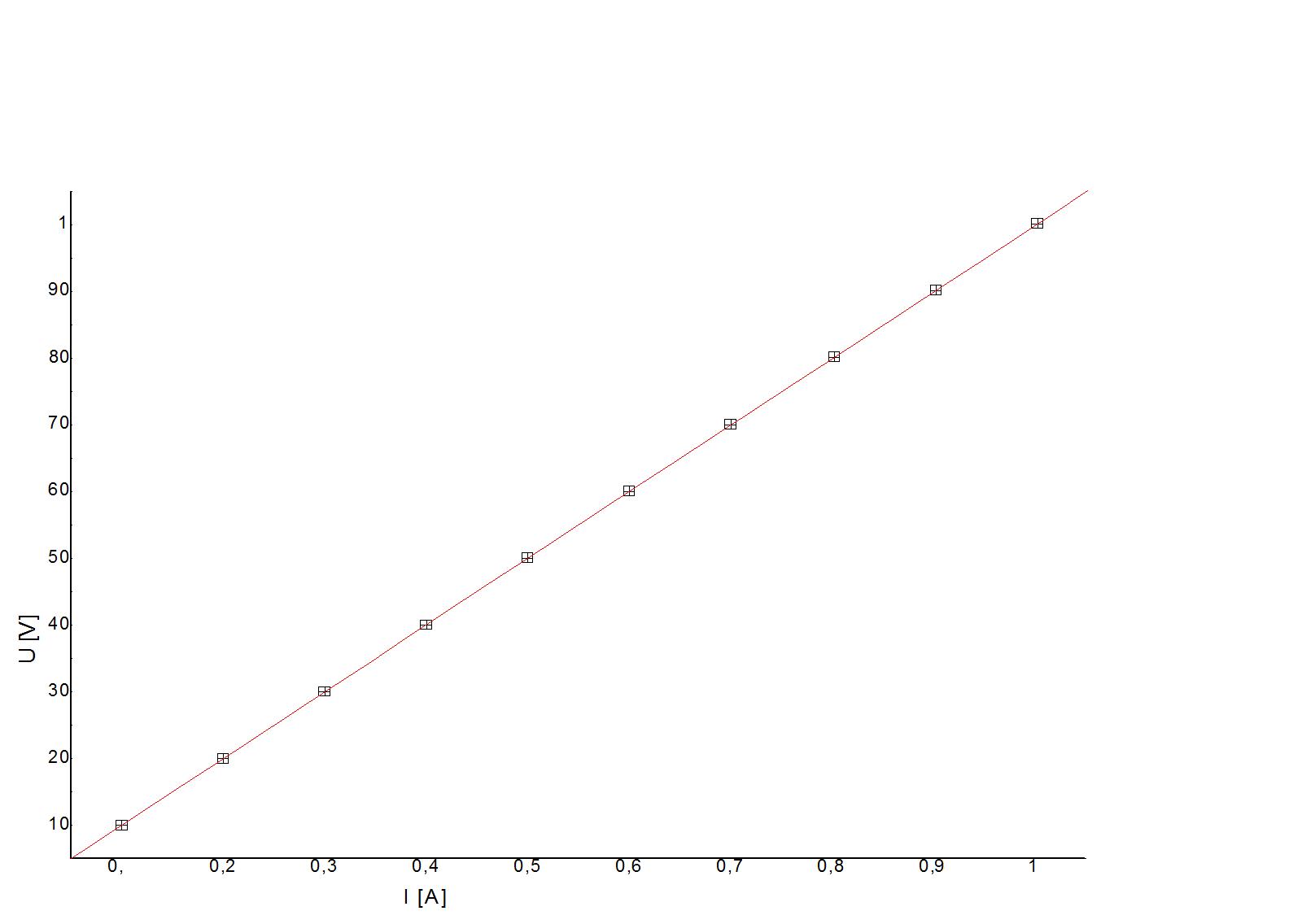
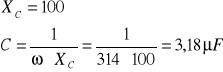
Mogę teraz przystąpić do wyliczenia pojemności kondensatora:
![]()
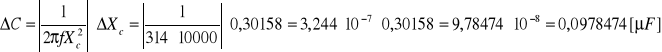
Wniosek: Podana przez program Origin wartość rezystancji cewki dla prądu stałego wynosi
16,8±0,1 [Ω], wartość rezystancji pozornej cewki dla prądu zmiennego podana przez program 63,5±0,2 [Ω], wyliczona wartość indukcyjności cewki dla prądu zmiennego o częstotliwości f=50Hz wynosi 0,195± 0,001[H], natomiast obliczona pojemność kondensatora jest równa 32,1±0,1 [µF]. Wydaje się to być bardzo prawdopodobnym wynikiem, ponieważ odczytana pojemności kondensatora wynosi 3,2[µF].
Wyszukiwarka