WEAiIE |
Biegański Marek Madej Marek |
Grupa I |
Zespół 11 |
|||
Laboratorium Fizyczne |
Temat: Przerwa energetyczna w germanie |
Nr ćwiczenia: 122 |
||||
Data wykonania: 20.05.1999 |
Data oddania:
26.05.1999 |
Zwrot do poprawy: |
Data odbioru: |
Data zaliczenia: |
Ocena: |
|
1. Cel ćwiczenia
Celem ćwiczenia jest wyznaczenie szerokości przerwy energetycznej w monokrysztale - w germanie - przez pomiar zależności jego oporu od temperatury.
2. Wprowadzenie teoretyczne
German jest tzw. półprzewodnikiem, czyli należy do grupy materiałów, które w temperaturze bliskiej zera bezwzględnego są izolatorami, natomiast w wyższych temperaturach posiadają wartość przewodności pośrednią między metalami i izolatorami. Półprzewodnikami są więc kryształy atomowe, które w temperaturze zera bezwzględnego możemy uważać za izolatory, ponieważ mają całkowicie zapełnione pasmo walencyjne i zupełnie puste pasmo przewodzenia, ale które mają przerwę energetyczną pomiędzy oboma pasmami nie większą niż 2 eV. Dla germanu przerwa ta (wg tablic) wynosi ok. 0.67 eV więc jest on dobrym przykładem półprzewodnika. Przewodnictwo półprzewodnika wzrasta gwałtownie ze zmianą temperatury, ponieważ każde wzbudzenie elektronowe do pasma przewodnictwa pozostawia dziurę w paśmie walencyjnym.
Przewodnictwo półprzewodnika powstające dzięki wzbudzeniom termicznym zwane jest przewodzeniem samoistnym. Istnieją też inne sposoby zwiększenie przewodnictwa, jak np.: przez wzbudzenie światłem (fotoprzewodnictwo). Przerwa energetyczna w półprzewodnikach określająca minimalną energie wzbudzenia, odpowiada energii fotonów z czerwonego czy podczerwonego obszaru widma elektromagnetycznego - dzięki temu przewodnictwo elektryczne półprzewodników wzrasta wraz ze wzrostem oświetlenia. Jeszcze innym sposobem zwiększenia przewodnictwa jest stosowanie domieszek do półprzewodnika. Polega to na zastąpieniu niektórych atomów w półprzewodniku atomami innego pierwiastka, mającymi w przybliżeniu takie same rozmiary, ale inną liczbę elektronów walencyjnych. Wynikające z tego przewodnictwo zwane jest przewodnictwem niesamoistnym, a procedurę taką nazywamy domieszkowaniem.
Przykładowo: jeśli niewielką ilość arsenu dodamy do stopionego germanu to domieszki arsenu będą miały wraz z germanem strukturę diamentu. Ponieważ arsen ma 5 elektronów walencyjnych a german tylko cztery, więc po utworzeniu wiązania kowalentnego german-arsen jeden z elektronów walencyjnych arsenu pozostanie wolny. Nie może on znaleźć się w paśmie walencyjnym i jest dosyć słabo związany na orbicie. Może więc oderwać się łatwo i przejść do pasma przewodzenia w temperaturze znacznie niższej od tej jaka byłaby potrzebna aby wyrwać jeden z elektronów pasma walencyjnego. Jest to związane z tym, że do wyrwania tego elektronu jest potrzebna dużo mniejsza energia, bowiem jego energia wiązania jest niewielka. W normalnych temperaturach wszystkie te elektrony przechodzą do pasma przewodzenia. Przewodnictwo elektronowe może być łatwo kontrolowane przez ilość wprowadzanych domieszek arsenu. Domieszka, która dostarcza wolnych elektronów nazywana jest donorem, a otrzymany przewodnik jest przewodnikiem typu n (od ang. negative - ujemny), ponieważ posiada nadmiar swobodnych elektronów.
Jeśli zaś do germanu dodamy niewielką ilość galu sytuacja będzie diametralnie różna od poprzedniej. Gal ma 3 elektrony walencyjne, więc przy tworzeniu wiązań kowalencyjnych zabraknie jednego elektronu na atom. Rezultatem tego jest dziura, która zachowuje się jak cząstka o dodatnim ładunku i masie, która może się poruszać w krysztale, gdyż kolejne elektrony zapełniając jedną dziurę tworzą natychmiast następną. Ruch elektronów jest więc jednocześnie ruchem dziur w krysztale. Z energetycznego punktu widzenia domieszka ta daje nieobsadzone poziomy dyskretne nieco powyżej wierzchołka pasma walencyjnego. Elektrony walencyjne mogą być łatwo wzbudzane do tych domieszkowych poziomów, na których mogą pozostać, zostawiając dziury w paśmie walencyjnym. Domieszka mająca za mało elektronów nazywana jest akceptorem, a otrzymany półprzewodnik - półprzewodnikiem typu p (od ang. positive - dodatni).
Wykres poziomów energetycznych półprzewodnika, podobnie zresztą jak i izolatora, charakteryzuje obecność przerwy energetycznej energii, której nie mogą zajmować elektrony. Jest to tzw. pasmo wzbronione. Przerwa energetyczna oddziela pasmo walencyjne (w niskich temperaturach całkowicie wypełnione przez elektrony) od pustego pasma przewodzenia. W przeciwieństwie do izolatora, w półprzewodnikach szerokość przerwy energetycznej Eg jest mała. Ze wzrostem temperatury część elektronów zostaje wzbudzona do pasma przewodnictwa i staje się elektronami swobodnymi. W paśmie walencyjnym powstaje więc taka sama dodatnich nośników prądu - dziur.
Zależność koncentracji elektronów swobodnych n i dziur p od temperatury dla półprzewodnika samoistnego (bez domieszek) można wyprowadzić korzystając z pojęć teorii pasmowej.
Liczba stanów w danym przedziale energii dE jest pierwiastkową funkcją energii, liczonej od pasma przewodzenia lub wierzchołka pasma walencyjnego. Obrazowo przedstawia tą zależność wykres 2a. Proporcjonalność tą zapisujemy:
g(E) ∼ E1/2.
Prawdopodobieństwo obsadzenia stanu przez elektron podaje funkcja rozkładu Fermiego - Diraca:
W naszym uproszczonym modelu, w którym pasmo walencyjne jest symetrycznym odbiciem pasma przewodzenia, poziom Fermiego EF znajduje się w połowie szerokości przerwy energetycznej. Liczba elektronów w przedziale energii dE jest więc równa g(E)p(E)dE. Całkowitą liczbę elektronów można obliczyć przez scałkowanie tej wielkości po całej szerokości pasma przewodzenia
Dla zwykłych przewodników dla których E - EF >> kT, dlatego w powyższym wzorze jedynkę w mianowniku można pominąć, co umożliwia łatwe obliczenie całki metodą przez podstawianie:
Przyjmujemy:
E/kT = x dE = kTdx
Otrzymujemy więc:
(1)
Ostatnie wyrażenie podcałkowe oznacza pewną liczbę rzeczywistą, której nie warto obliczać, bowiem wpływa ona tylko na nieznany współczynnik proporcjonalności. Jak wynika z rysunku, że w wybranej skali energii, w której za zero przyjęte jest dno pasma przewodnictwa, EF = - 0.5 Eg, gdzie Eg jest szerokością przerwy energetycznej. Zależność koncentracji nośników od temperatury przybiera zatem postać:
(2)
Przewodność właściwa półprzewodnika jest określona wzorem:
σ = e n μn + e p μp
gdzie e oznacza ładunek elementarny, zaś μn i μp - odpowiednio ruchliwości elektronów i dziur.
Przewodnictwo zmienia się z temperaturą zarówno za skutek opisanego równaniem (2) wzrostu liczby nośników prądu, jak i zmiany ich ruchliwości.
Ruchliwość nośników w przewodnikach, podobnie jak w metalach, maleje ze wzrostem temperatury na skutek oddziaływania z drganiami sieci krystalicznej. Spadek ruchliwości prawie całkowicie kompensuje czynnik T3/2 we wzorze (2) i w rezultacie temperaturowa zależność przewodności właściwej względnie oporu elektrycznego (R ∼ 1/σ) jest opisana przez czynnik wykładniczy:
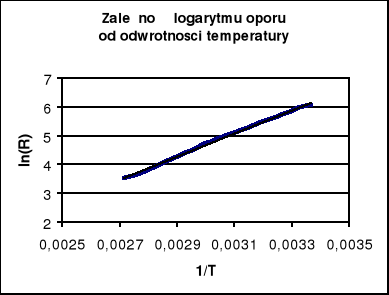
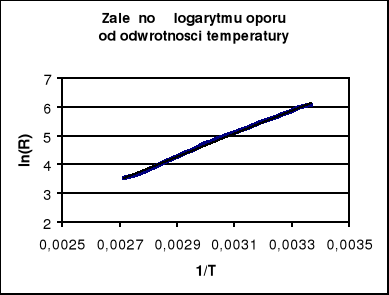
W celu uzyskania wartości Eg wyniki pomiarów oporności monokryształu germanu w funkcji temperatury przedstawiamy w formie:
Wykres zależności lnR w funkcji 1/T przedstawia prostą, której współczynnik nachylenia a jest proporcjonalny do szerokości przerwy energetycznej
a = Eg / 2k
Wartość współczynnika obliczono korzystając z metody najmniejszych kwadratów.
3. Wyniki pomiarów i ich opracowanie
k = 1,381e-23 - stała Boltzmana
t - przybliżona temperatura germanu,
R - zmierzony opór półprzewodnika,
n - ilość pomiarów.
GERMAN
Pomiar |
t [°C] |
T [K] |
R [Ω] |
1/T = x |
ln R = y |
x2 |
x • y |
1 |
24 |
297,16 |
434,7 |
0,003365 |
6,07465 |
1,13E-05 |
0,020442 |
2 |
25 |
298,16 |
428,2 |
0,003354 |
6,05959 |
1,12E-05 |
0,020323 |
3 |
30 |
303,16 |
353,0 |
0,003299 |
5,86646 |
1,09E-05 |
0,019351 |
4 |
35 |
308,16 |
285,1 |
0,003245 |
5,65284 |
1,05E-05 |
0,018344 |
5 |
40 |
313,16 |
237,5 |
0,003193 |
5,47016 |
1,02E-05 |
0,017468 |
6 |
45 |
318,16 |
198,7 |
0,003143 |
5,29179 |
9,88E-06 |
0,016632 |
7 |
50 |
323,16 |
164,5 |
0,003094 |
5,10291 |
9,58E-06 |
0,015791 |
8 |
55 |
328,16 |
136,7 |
0,003047 |
4,91778 |
9,29E-06 |
0,014986 |
9 |
60 |
333,16 |
116,0 |
0,003002 |
4,75359 |
9,01E-06 |
0,014268 |
10 |
65 |
338,16 |
91,2 |
0,002957 |
4,51305 |
8,74E-06 |
0,013346 |
11 |
70 |
343,16 |
77,1 |
0,002914 |
4,34510 |
8,49E-06 |
0,012662 |
12 |
75 |
348,16 |
64,2 |
0,002872 |
4,16200 |
8,25E-06 |
0,011954 |
13 |
80 |
353,16 |
51,5 |
0,002832 |
3,94158 |
8,02E-06 |
0,011161 |
14 |
85 |
358,16 |
43,8 |
0,002792 |
3,77963 |
7,8E-06 |
0,010553 |
15 |
90 |
363,16 |
37,7 |
0,002754 |
3,62966 |
7,58E-06 |
0,009995 |
16 |
95 |
368,16 |
33,5 |
0,002716 |
3,51154 |
7,38E-06 |
0,009538 |
|
|
|
Suma |
0,048579 |
77,07239 |
0,000148 |
0,236814 |
Na podstawie znalezionych warto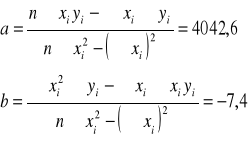
ści a i b można znaleźć błąd wartości a:
Pomiar |
(y-(ax+b))2 |
1 |
0,00523152 |
2 |
0,00174452 |
3 |
0,00012695 |
4 |
0,00007275 |
5 |
0,00033323 |
6 |
0,00182811 |
7 |
0,00254685 |
8 |
0,00313030 |
9 |
0,00587278 |
10 |
0,00024071 |
11 |
0,00047311 |
12 |
0.00061400 |
13 |
0,00232241 |
14 |
0,00253363 |
15 |
0,00201647 |
16 |
0,00014011 |
Suma: |
0,02867490 |
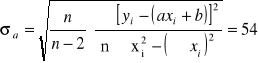
Tak więc współczynnik nachylenia prostej wynosi a = 4042 ± 54.
Korzystając z wyprowadzonych wcześniej zależności możemy obliczyć wartość przerwy energetycznej w germanie:
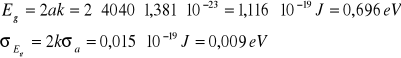
Eg = 0,696 (9) eV
TERMISTOR
Pomiar |
t [°C] |
T [K] |
R [Ω] |
1/T = x |
ln R = y |
1 |
24 |
297,16 |
360,1 |
0,003365 |
5,88638 |
2 |
25 |
298,16 |
345,9 |
0,003354 |
5,84615 |
3 |
30 |
303,16 |
268,0 |
0,003299 |
5,59098 |
4 |
35 |
308,16 |
197,3 |
0,003245 |
5,28472 |
5 |
40 |
313,16 |
162,5 |
0,003193 |
5,09067 |
6 |
45 |
318,16 |
137,7 |
0,003143 |
4,92507 |
7 |
50 |
323,16 |
115,4 |
0,003094 |
4,74840 |
8 |
55 |
328,16 |
96,1 |
0,003047 |
4,56538 |
9 |
60 |
333,16 |
83,0 |
0,003002 |
4,41884 |
10 |
65 |
338,16 |
67,6 |
0,002957 |
4,21360 |
11 |
70 |
343,16 |
58,7 |
0,002914 |
4,07244 |
12 |
75 |
348,16 |
50,3 |
0,002872 |
3,91800 |
13 |
80 |
353,16 |
40,9 |
0,002832 |
3,71113 |
14 |
85 |
358,16 |
35,0 |
0,002792 |
3,55534 |
15 |
90 |
363,16 |
31,0 |
0,002754 |
3,43398 |
16 |
95 |
368,16 |
28,0 |
0,002716 |
3,33220 |
- 6 -
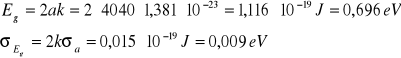
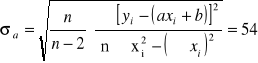
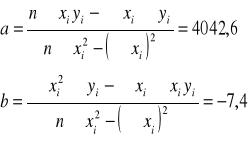
Wyszukiwarka