Z1
1. Wymień siły działające w cieczach.
Na płyn mogą działać siły powierzchniowe(zwane także ciśnieniowymi) - ściskające, - styczne oraz objętościowe (zw. masowymi)- bezwładności, -de Lamberta i siły styczne.
2. Podaj równanie ciągłości dla przepływu ustalonego płynu ściśliwego.
Równanie ciągłości: ρ1·V1·F1=ρ2· V2·F2=const. Q1=Q2 Q1= ρ1·V1·F1 Q2=ρ2·V2·F2
3. Podaj definicję lepkości cieczy.
Lepkość cieczy jest to właściwość polegająca na stawianiu oporu przy wzajemnym przesuwaniu się cząsteczek względem siebie. Własność tą ma jedynie ciecz znajdująca się w ruchu, a zależy ona od rodzaju cieczy i jej temperatury. W obliczeniach praktycznych posługujemy się tzw. kinematycznym współczynnikiem lepkości, który jest ilorazem dynamicznym μ i gęstości cieczy ρ
Wartości te podawane są tabelarycznie.
4. Podaj od jaki czynników zależy ilość energii przekazanej cieczy w obrębie wirnika pompy odśrodkowej.
Przyrost energii płynu w obrębie wirnikia odniesiony do jednostki masy zależy od:
prędkości obrotowej,
promienia wirnika,
kąta ustawienia łopatek.
5. Przedstaw graficznie regulację upustową.
Zadanie:
1. Do obydwu ramion częściowo wypełnionej rtęcią U-rurki wlano dwie różne ciecze o gęstościach ρ1i ρ2
tak, że ich wysokość nad poziomem rtęci w ramionach jest jednakowa i wynosi H. Oblicz różnicę poziomów rtęci.
Zad. 2.
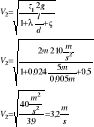
Oblicz prędkość wody wypływającej z otwartego zbiornika poziomą, gładką rurką o średnicy d=5mm i długości l=5m, jeżeli wiadomo, że wysokość słupa cieczy nad osią przewodu wynosi h=2m, ς0=0,5 a lepkość dynamiczna wody wynosi μ=0,001kg/sm
D
h d
l = 5 m
d = 5 mm
h = 2 m
μ = 0,001kg/sm
V1 = ?
D >> d ⇒V1 = 0
λ=f(Re)=f(V2)
należy zastosować metodę kolejnych przybliżeń:
1. Zakładamy dokładność obliczeniową:
ε = 0,2≤|V2n-1 + V2n|
2. zakładamy V2 = 3m/s
3. obliczamy Re
5. Podstawiamy λ do wzoru:
6. sprawdzamy
|3,2 - 3| = 0,2 = ε
Odp: Prędkość w wypływającej wody wynosi
V2 = 3,2 m/s
Zadanie 3:
Oblicz jaka powinna być oporność linii upustowej, aby wydatek wody tłocznej przez pompę M8/8 do pojedynczej linii W75 o długości l=2000m, zakończonej prądownicą φ13 zmalał o połowę.
Dane:
S075 = 0,001s2/dm6
S13 = 2,89 ms2/dm6
H =A - AQ2
Hmax = 120 m
Qmax = 20 dm3/s
A = Hmax = 120 m
Q' = 0,5 ∙ Q =0,5 ∙ 4,8 dm3/s
Q' = 2,4 dm3/s
Odp:
Aby wydatek zmalał o połowę należy uzyskać straty na upuście wielkości
0,124 ms2/dm6
Zestaw 2
1. Podaj równanie Eulera i warunek równowagi cieczy.
2. Wykaż, że środek naporu na dowolną ścianę pochyłą leży poniżej środka ciężkości figury jaką tworzy dana ściana.
Ad 2. Przyrost wysokości ciśnienia P/H - P0/H = z jest równy głębokości zanurzenia i jest do niego wprost proporcjonalny. Napór N na ściankę naczynia N=H∙z∙F
F - pow. Ścianki, z - głębokośsc zanurzenia jej środka ciężkości tworzącego środek naporu hydrostatycznego, a nie środka geometrycznego który leży nieco powyżej.
3. O czym świadczy równość liczb Reynoldsa w dwóch różnych przepływach?
Równość liczb Reynoldsa świadczy o tym, że mamay do czynienia z takim samym ruchem np laminarnym Re<2320 lub burzliwym Re>2320 panującym w przewodzie.
Lub, że opory w tych przepływach spowodowane są wyłącznie lepkością.
4. Podaj zależność na straty liniowe.
Straty liniowe:
λ - współczynnik oporów liniowych bezwymiarowy zależy od lepkości cieczy,
l/d - wymiary geometryczne przewodu,
V2 - prędkość przepływu do kwadratu
Straty miejscowe
5. Na czym polega regulacja pomp wirowych ?
Regulacja pomp wirowych w praktyce sprowadzasię do zmiany punktu pracy pompy. Zmiane tę możemy osiągnąć poprzez :
zmianę charakterystyki przewodu (dławienie, upust),
zmianę charakterystyki pompy (zmiana prędkości obrotowej)
w większych pompach regulujemy również poprzez zmianę kąta udstawienia łopatek wirnika.
Zad. 1. Oblicz wielkość naporu wody na płaską kwadratową klapę o boku a, usytuowaną na płaskiej ścianie zbiornika nachylonej pod kątem α = 450 do poziomu, jeżeli głębokość zanurzenia jej
Nz = ρgV
V = b∙a∙h - ¼ π∙a2∙b
V = b∙a(h- ¼ π∙a)
Nz = ρ∙g∙a∙b(h- ¼ π∙a)
Nx = ρ∙g∙Zs∙F'
Zad. 2 Woda wypływa poziomą rurką o długości l=2m i srednicy d z otwartego naczynia. Wiedząc, że wysokość cieczy poinad osią rurki wynosi 2m oraz współczynnik strat lokalnych na wlocie dorurki wynosi
ς=0,5. Określ maksymalną średnicę, przy którejprzepływ będzie laminarny. Przyjąć μ=0,001kg/sm
Dane:
ς = 0,5
μ = 0,001kg/sm
l = 2m
h = 2m
D>>d⇒V1=0
z1 = h
z2 = 0
p1 = p2 = pbar
O zasięgu strumienia zwartego decydują:
- średnica pyszczka prądownicy,
- ciśnienie na pyszczku prądownicy,
- kąta pod jakim ustawimy prądownicę podczas podawania zwartego prądu wody.
Hpr -ciśnienie wylotowe
φpr - współczynnik zależny od średnicy pyszczka
d - srednica pyszczka w [mm].
5. Wyprowadz zależność na oporność zastępczą dwóch idenycznych przewodów
ułożonych równolegle w płaskim terenie.
QC = Q1 + Q2
∆hstr = Sz ∙ QC2
∆hstr1 = Sz1 ∙ Q12
∆hstr2 = Sz2 ∙ Q22
Zad. 1. Określić składowe i wypadkową siłę naporu działającą na powierzchnię dna naczynia o kształcie prostopadłościanu o wymiarach axbxh, jeżeli wiadomo, że powierzchnia ta stanowi ¼ walca o promieniu a i wysokości b a jej oś leży w
płaszczyźnie boku o wymiarach bxh w odległości a od dna.
Pierwiastek musi spełniać:
0> Q2 > Qp
Zest. 3.
1. Od czego zależy napór na ścianę zakrzywioną dowolnie zorientowaną w przestrzeni?
Napór na ścianę zakrzywioną dowolnie zorientowaną w przestrzeni zależy od wartości składowych pionowej Nz i poziomej Nx N=√Nz2+Nx2
Składowa pionowa naporu na ścianę zakrzywioną jest co do modułu równa ciężarowi słupa cieczy zawartego między rozpatrywaną ścianą a lustrem cieczy Nz=ρgV składowa pozioma naporu na ścianę zakrzywioną jest równa naporowi na rzut tej ściany na dowolną płaszczyznę pionową Nx=ρgZsF'
2. jaka jest różnica pomiędzy przepływem ustalonym i nieustalonym?
Przepływem ustalonym (trwałym) nazywamy taki ruch, jeżeli wszystkie elementy ruchu zależą wyłącznie od położenia cząsteczki, a nie zależą od czasu, czyli nie ulegają w czasie żadnym zmianom.
Przepływ nazywamy nieustalonym (nietrwałym), gdy pewne elementy ruchu zmieniają się w czasie.
Przepływ ustalony dzieli się jeszcze na przepływ jednostajny i niejednostajny (zmienny).
Przepływ nazywamy jednostajnym, kiedy wszystkie przekroje poprzeczne strumienia są takie same, a w odpowiednich punktach tych przekrojów panują jednakowe prędkości.
Przepływ nazywamy niejednostajnym, gdy przekroje poprzeczne strumienia są różne, a więc i prędkości niejednakowe.
3. Udowodnij, że w poziomym przewodzie o stałej średnicy przez który przepływa płyn nieściśliwy straty powodują jedynie zmniejszenie ciśnienia satycznego.
Na pokonanie oporów tarcia zużywa się energię ciśnienia, wskutek czego w czasie przepływu poziomego następuje spadek ciśnienia statycznego. Nazywa się stratą ciągłą.
4. Jakie czynniki decydują o zasięgu strumienia zwartego
Zad. 3. Określ wydatki i ciśnienia na prądownicach φ 13 zasilanych z motopompy M8/8, każda odzielną linią W75 przyjmując l1 = 500m, i l2 =1000m oraz różnicę wysokości między pompą a drugą prądownicą Δh = 10m
Dane:
S075 = 0,001s2/dm6
S13 = 2,89ms2/dm6
l1 = 500m
l2 =1000m
Δh = 10m
H = A - BQ2
Hmax = 120m,
Qmax = 20 dm3/s
Dolna gałąź Q1
Górna gałąź Q2
Q1+Q2=Qp
SzI∙Q12=SsII∙Q22
Q1= Qp - Q2
SzI ∙(Qp- Q2)= SsII∙Q22
SsI∙(Qp2- 2QpQ2 + Q22)-
- SsII∙Q22 = 0
SsI∙Qp2- SsI2QpQ2+ SsIQ22-
- SsII∙Q22 = 0
Q22(SsI- SsII)-Q2∙SsI2Qp + +SsI∙Qp2=0
środka geometrycznego wynosi h. Oblicz położenie środka naporu.
Zad 2.
Określ ciśnienie na króćcu ssawnym pompy pracującej z wydatkiem 0,01m3/s jeżeli wiadomo, że geometryczna wysokość ssania wynosi 6m, przewód ssawny ma długość 10 m, średnicę 0,1m i wewnętrzną powierzchnię gładką, łączny współczynnik lepkości dynamicznej μ = 0,001 kg/sm Dane:
d = 0,1m
μ = 0,001 kg/sm
l = 10 m
Q = 0,01 m3/s
hss = 6 m
Przepływ laminarny dla Re≤2320 to λ = 0,026
Średnica jest funkcją prędkości i należy zastosować metodę kolejnych przybliżeń.
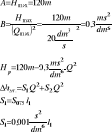
Zad. 3.Pompa M8/8 zasila układ węży składający się z linii głównej W75 o długości l1=400m, rozdzielacza i trzech linii gaśniczych W52 o długości l2=40m każda, zakończonych prądownicą φ12. Oblicz ciśnienie i wydatki na prądownicach. Określ przy jakiej różnicy wysokości rozpatrywany układ zapewnia uzyskanie optymalnych ciśnień na prądownicach.
Dane:
S075 = 0,001s2/dm6
S052 = 0,0054s2/dm6
S12 = 4,0 ms2/dm6
H =A - AQ2
Hmax = 120 m
Qmax = 20 dm3/s
Odp. Przy takim układzie nie jesteśmy w stanie uzyskać optymalnych ciśnień na prądownicach, chyba, że prądownice będą 16,5m poniżej pompy.
Zestaw 4.
1.Określ warunkim w jakich obowiązuje Prawo Pascala .
Prawo Pascala obowiązuje tylko wówczas gdy na ciecz będącą w równowadze nie działają żadne inne siły oprócz powierzchniowych. Wówczas ciśnienie w każdym punkcie płynu jest takie same.
2. Jak definiujemy predkość średnią strumienia?
W wypadku ruchu laminarnrgo w prostym przewodzie kołowym cząsteczki poruszają się po torach równoległych do osi rury, zaś samo zjawisko ruchu odbywa się bez jakichkolwiek zaburzeń. Warstewki cieczy przylegające bezpośrednio do ścianek przewodu będą miały prędkość bliską zeru, zaś najszybciej płynąć będą cząsteczki w osi przewodu.
Vśr.=Vmax/2 w ruchu laminarnym zaś w ruchu burzliwym Vśr.=0,83Vmax
4. Podaj definicję wzlotu strumienia zwarteg. Od czego zależy wzlot?
Wzlotem strumienia zwartego nazywamy wysokość do której maksymalnie może wzlecieć woda przy pionowym ustawieniu prądownicy.
5. Podaj równanie charakterystyki zastępczej dwóch identycznych pomp pracujących szeregowo.
Hp = A -B Q2
gdzie A = Hmax
Zad. 1.
Prodstopadłościenne naczynie którego podstawę stanowi kwadrat o boku a=0,02m wypełniono do wysokości h1=0,2m rtęcią, a następnie wlano do niego wodę, tak, że odległość lustra wody od dna wynosi h2=0,5m. Przyjmując ρrtęci=13600kg/m3 oraz ρwody=1000kg/m3 oblicz napór na część ściany bocznej stykającej się z rtęcią.
F = 0,2m x 0,02 m = 0,04m2
N = ρ∙g∙Zs∙F
Zad. 2. Przyjmując że dla gwałtownego rozszeżenia przewodu ς =[1-(d1/d2)2]2, określić warunki przy których ciśnieniestatyczne w miejscu gwałtownego rozszeżenia nie zmieni się.
Zad.3. Określić jaka powinna być oporność dodatkowego elementu dławiącego przepływ(zaworu), aby wydatek pompy M8/8 zasilający układ składający się z lini głównej W75 o długości L1=1000m, rozdzielacza i dwóch lini gaśniczych W52 o długości L2=40m zakończonych prądownicami φ13 zmniejsył się o połowę. Przyjąć że różnica poziomów pompy i prądownic wynosi ΔH=10m.
Dane:
S075 = 0,001s2/dm6
S052 = 0,0054s2/dm6
S13 = 2,89 ms2/dm6
H =A - AQ2
Hmax = 120 m
Qmax = 20 dm3/s
Odp. Aby zmniejszyś wydatek o połowę, oporność dodatkowa musi wynosić 6,4ms2/dm6.
Zestaw 5.
1. Wykaż, że ciśnienie jest wielkością skalarną.
W płynie pozostającym w równowadze względem ścian naczynia ciśnienie na element powierzchniowy, umieszczony w dowolnym punkcie nie zależy od przestrzeni orientacji tego elementu. To tzw. prawo niezależności
ciśnienia od orientacji elementu powierzchniowego, sformuowane przez Eulera, wyraża po prostu fakt, że ciśnienie w cieczy ma charakter skalarny (bezkierunkowy).
2. W jaki sposób w oparciu o równanie Eulera można wykazać, że przesunięcie po powierzchni ekwipotencjalnej nie wymaga żadnej pracy.
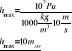
3. Określ teoretyczną wysokość ssania.
Teoretyczna wysokość ssania jest to najwyższa wysokość ssania obliczona teoretycznie dla cieczy doskonałej. Obliczana jest ze wzoru
Wysokość ssania jest maksymalna gdy pod tłokiem występuje stan graniczny tj. p=0 p=pa- ρgh
Jeżeli pa=105Pa; g=10m/s2; ρ=1000kg/m3 to:
Jak widać teoretyczna wysokość ssania jest zależna
Długość L2 jest funkcją ΔH dlatego należy zastosować metodę kolejnych przybliżeń.
poziomem pompy na wysokości ΔH. Określ warunek ze względu na L1 i ΔH, przy którym możliwe
będzie uzyskanie na prądownicach co najmniej ciśnień optymalnych.
Dane:
S075 = 0,001s2/dm6
S052 = 0,0054s2/dm6
S12 = 4,0 ms2/dm6
H =A - AQ2
Hmax = 120 m
Qmax = 20 dm3/s
z1 = z2 = 0
D>>d⇒ V = 0
Zad. 3. Motopompa M8/8 zasila układ złożony z linii głównej W75 o długości L1, rozdzielacza i trzech linii gaśniczych W52 o długości L2=40m zakończonych prądownicami φ12. Prądownice znajdują się ponad
od ciśnienia atmosferycznego i gęstości cieczy zasysanej.
4. Określ teoretyczny współczynnik strat dla prądownicy φ12 pryjmując μ=1,0.
5. Przedstaw graficznie regulację dławieniem.
Zad. 1. Oblicz składowe i wypadkową siłę naporu wody działającej na dno walcowatego naczynia o wysokości h i promieniu r, jeżeli wiadomo, że dno ma kształt półkuli zwróconej wypukłością ku górze.
Objętość kuli
V=4/3 πr3
Powierzchnia dna:
P= ½ πd2 = 2 πr2
Składowa pionowa:
Nz = ρgV
Składowa pozioma:
Nx = ρ∙g∙Zs∙ A'
V= πr2∙ h - 2/3 πr3
V= πr2(h - 2/3r)
Zs= h/r
Nz = ρ∙g∙ πr2(h - 2/3r)
Nx = ρ∙g∙ A'∙ (h - r/2)
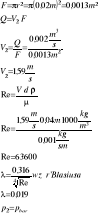
Zad. 2. W zbiorniku hydroforowym ciśnienie powietrza wynosi p=0,5MPa
. Określić maksymalną odległość na jaką można dostarczyć poziomym, gładkim przewodem o średnicy d=0,04m wydatek 2.0dm3/s. Przyjąć sumaryczny współczynnik strat lokalnych ς=2,0 oraz μ=0,001kg/sm.
P1=0,5MPa
D =0,04m ⇒ r = 0,02m
Q = 2dm3s
ς=2,0
μ=0,001kg/sm
![]()
H
Qc = Q
Qp
Qn
Q
Hp = f(Q)
ΔHstr=f(Q)Sz·Qu2
ΔHstr=Sz· Qu2
M = const
h
a
ρ2
ρ1
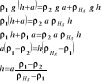
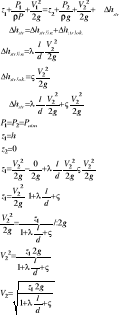
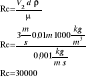
P
M8/8
L=2000m
upust
S13
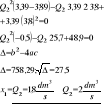
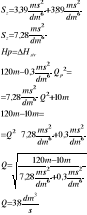
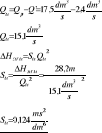
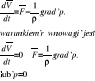
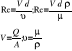
![]()
![]()
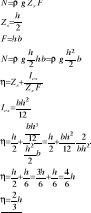
h ys
η H
α
N
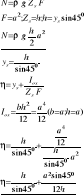
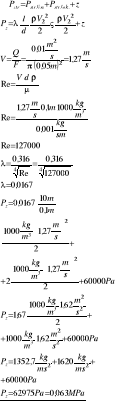
P
hss
Δhstr.
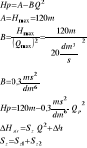
Δh
W75 l1 = 500m
P
W75 l2 = 1000m
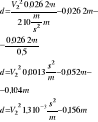
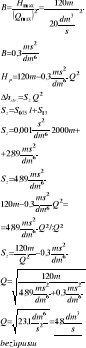
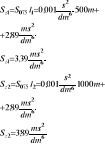


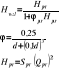
![]()
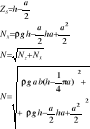
Q1
S=S01∙l1+Spr
Q2
S=S02∙l2+Spr
Qc
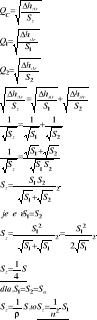
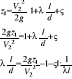
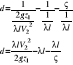


h
D
h
d
b
a

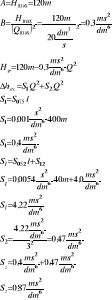
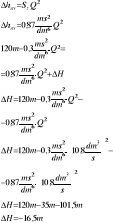
h/3
a
a
h/2
W75 l1 = 1000m
P

P
P
2hmax
hmax
h
h
H
h
h
Q
ΔHstr=Sz· Qu2
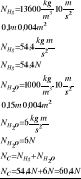
W52 l2 = 40m
![]()
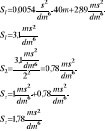
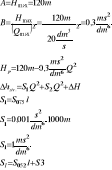
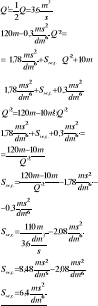

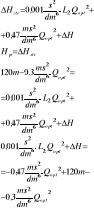
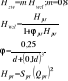
H
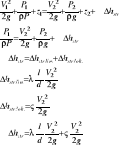
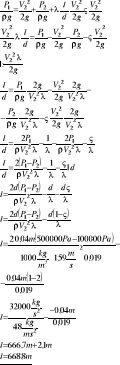
ΔHstr=(Sz+SREG) Qu2+ΔH
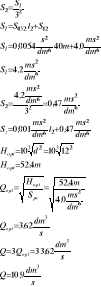

Q
ΔH
ΔQ
H
ΔHstr=f(Q)
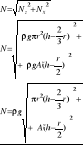
P1
d
D
Wyszukiwarka