Laboratorium Podstaw Fizyki
Nr ćwiczenia 53
Temat ćwiczenia: Prawo Ohma dla prądu przemiennego.
Nazwisko i Imię prowadzącego kurs: dr inż. T. Wiktorczyk
Wykonawca |
|
Imię i Nazwisko nr indeksu, wydział |
Ewelina Turek 185426 Martyna Zalewska 185146 Wydział Chemiczny |
Termin zajęć: dzień tygodnia, godzina |
Czwartek 17:05-18:45 |
Numer grupy ćwiczeniowej |
|
Data oddania sprawozdania |
17.03.2011 |
Ocena końcowa |
|
Zatwierdzam wyniki pomiarów.
Data i podpis prowadzącego zajęcia:
Adnotacje dotyczące wymaganych poprawek oraz daty otrzymania
poprawionego sprawozdania
1. Cel ćwiczenia
Sprawdzenie słuszności prawa Ohma poprzez analizę zależności natężenia prądu od napięcia Usk=f(Isk) dla układów RC, RL i RLC - wyznaczenie zawady tych układów oraz obliczenie wartości C i L.
Wstęp teoretyczny
Prąd przemienny (ang. alternating current, AC) - charakterystyczny przypadek prądu elektrycznego okresowo zmiennego, w którym wartości chwilowe podlegają zmianom w powtarzalny, okresowy sposób, z określoną częstotliwością. Wartości chwilowe natężenia prądu przemiennego przyjmują naprzemiennie wartości dodatnie i ujemne (stąd nazwa przemienny). Najczęściej pożądanym jest, aby wartość średnia całookresowa (tzn. składowa stała) wynosiła zero.
Jeżeli do zacisków układu złożonego z szeregowo połączonych: rezystancji R, pojemności C i indukcyjności L przyłożymy siłę elektromotoryczną sinusoidalnie zmienną:
E=E0sin t,
to w układzie popłynie prąd sinusoidalnie zmienny o natężeniu:
I=I0sin (t+),
gdzie
- przesunięcie fazowe między natężeniem prądu a siłą elektromotoryczną.
Między I0 i E0 zachodzi związek:
I0=E0/Z.
Powyższa zależność przedstawia prawo Ohma dla prądu przemiennego. Łatwo zauważyć, że rolę rezystancji w tym układzie prądu przemiennego spełnia Z zwane zawadą. Można wykazać, że jej wartość w takim układzie wynosi:
Z= R 2 + (L - 1/C)2
Jeżeli obwód składa się z połączonych szeregowo rezystancji R i indukcyjności L wówczas zawadę możemy opisać wzorem:
Z= R 2 + (L)2.
Przekształcając ten wzór możemy wyznaczyć indukcyjność L:
L= 1/2f (U/I)2 - (RL+R)2.
W przypadku obwodu zawierającego rezystancję R i pojemność C zawada wyraża się wzorem
Z= R2 + (1/C)2
Na podstawie tego wzoru możemy wyznaczyć pojemność C:
C= (2f (U/I)2 - R2 ) -1
Zestaw przyrządów
- Zestaw indukcyjności typ 2001 ZANiD
- Zestaw pojemności typ LIF - 04 - 114 - 2 ZANiD
- Opornik dekadowy kl. 0.1
- Autotransformator typ AM - 220
Rodzaj miernika |
Typ |
Dokładność przyrządu |
Amperomierz
|
Metex M3860D |
(± 2,5 % rdg + 3 dgt) |
Woltomierz
|
M890G |
± 0,8 % rdg + 3 dgt |
Zakres amperomierza: 400 [mA]
Zakres woltomierza: 200 [V]
Opór: 300 [Ω]
Autotransformator: f= 50Hz
Pomiary
Układ RC
1. Tabela pomiarów skutecznych wartości napięć Usk w zależności od skutecznych
wartości natężeń prądów oraz ich niepewności Isk w obwodzie RC.
Lp. |
Napięcie Usk [V] |
Niepewność pomiaru Usk |
Natężenie Isk [mA] |
Niepewność pomiaru Isk |
1. |
25 |
0,23 |
54,00 |
1,38 |
2. |
20 |
0,19 |
43,30 |
1,12 |
3. |
15 |
0,15 |
32,63 |
0,846 |
4. |
10 |
0,11 |
22,07 |
0,582 |
5. |
5 |
0,07 |
11,25 |
0,312 |
6. |
0 |
0,03 |
0,37 |
0,0393 |
Układ RL
2. Tabela pomiarów skutecznych wartości napięć Usk w zależności od skutecznych
wartości Isk ich niepewności w obwodzie RL.
Lp. |
Napięcie Usk [V] |
Niepewność pomiaru Usk |
Natężenie Isk [mA] |
Niepewność pomiaru Isk |
1. |
25 |
0,23 |
84,60 |
2,15 |
2. |
20 |
0,19 |
67,60 |
1,72 |
3. |
15 |
0,15 |
50,60 |
1,30 |
4. |
10 |
0,11 |
34,10 |
0,883 |
5. |
5 |
0,07 |
17,38 |
0,465 |
6. |
0 |
0,03 |
0,20 |
0,035 |
RL= 153 Ω
∆RL= 1 Ω
Układ RLC
3. Tabela pomiarów skutecznych wartości napięć Usk w zależności od skutecznych
wartości Isk ich niepewności w obwodzie RLC.
Lp. |
Napięcie Usk |
∆U |
Natężenie Isk |
∆Isk |
|
[V] |
[V] |
[mA] |
[mA] |
1. |
25,00 |
0,23 |
52,20 |
1,33 |
2. |
20,00 |
0,19 |
41,80 |
1,08 |
3. |
15,00 |
0,15 |
31,42 |
0,816 |
4. |
10,00 |
0,11 |
21,07 |
0,557 |
5. |
5,00 |
0,07 |
10,76 |
0,299 |
6. |
0,00 |
0,03 |
0,30 |
0,038 |
3. Wzory i przykładowe obliczenia
-Obliczanie średniej arytmetycznej:
Np. dla Usk:
![]()
-Obliczanie niepewności pomiaru
W przypadku pojedynczego pomiaru wielkości x niepewność pomiaru (∆x) wynika z dokładności przyrządu (δx)
∆x= δx
Np. dla ∆U1:
![]()
Układ RC
Lp. |
Napięcie Usk |
Niepewność pomiaru Usk |
Natężenie Isk |
Niepewność pomiaru Isk |
Z= (U/I) |
C |
∆C |
|
[V] |
[V] |
[mA] |
[mA] |
[Ω] |
[μF] |
[μF] |
1. |
25 |
0,23 |
54 |
1,38 |
462,963 |
9,032 |
0,548 |
2. |
20 |
0,19 |
43,3 |
1,12 |
461,894 |
9,068 |
0,247 |
3. |
15 |
0,15 |
32,63 |
0,846 |
459,700 |
9,144 |
0,257 |
4. |
10 |
0,11 |
22,07 |
0,582 |
453,104 |
9,379 |
0,266 |
5. |
5 |
0,07 |
11,25 |
0,312 |
444,444 |
9,712 |
0,303 |
6. |
0 |
0,03 |
0,37 |
0,0393 |
0,000 |
0 |
0 |
![]()
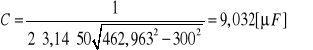

Układ RL:
Lp. |
Usk |
∆ Usk |
Isk |
∆Isk |
|
L |
∆L |
|
[V] |
[V] |
[mA] |
[mA] |
[Ω] |
[H] |
[H] |
1. |
25 |
0,23 |
84,6 |
2,15 |
295,51 |
Błąd w Pomiarach
|
Błąd w Pomiarach
|
2. |
20 |
0,19 |
67,6 |
1,72 |
295,86 |
|
|
3. |
15 |
0,15 |
50,6 |
1,3 |
296,45 |
|
|
4. |
10 |
0,11 |
34,1 |
0,883 |
293,26 |
|
|
5. |
5 |
0,07 |
17,38 |
0,465 |
287,69 |
|
|
6. |
0 |
0,03 |
0,2 |
0,035 |
0 |
|
|
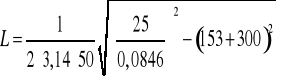
Brak rozwiązania, ponieważ nie można wyciągnąć pierwiastka kwadratowego z liczby ujemnej. Nie można również z tego powodu obliczyć ∆L.
Układ RLC:
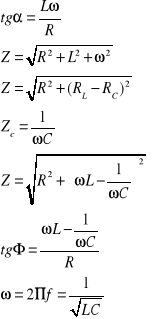
Ponieważ nie możemy wyliczyć L, skorzystałam ze wzoru powyżej i po kilku przekształceniach otrzymałam:
![]()
|
|
|
|
|
|
|
|
|
|
Lp. |
Napięcie Usk |
∆U |
Natężenie Isk |
∆Isk |
C |
tgɵ |
L |
|
|
[V] |
[V] |
[mA] |
[mA] |
|
|
|
|
1. |
25 |
0,23 |
52,2 |
1,33 |
9,032 |
0 |
1,12294E-06 |
|
2. |
20 |
0,19 |
41,8 |
1,08 |
9,068 |
0 |
1,11848E-06 |
|
3. |
15 |
0,15 |
31,42 |
0,816 |
9,144 |
0 |
1,10919E-06 |
|
4. |
10 |
0,11 |
21,07 |
0,557 |
9,379 |
0 |
1,08139E-06 |
|
5. |
5 |
0,07 |
10,76 |
0,299 |
9,712 |
0 |
1,04432E-06 |
|
6. |
0 |
0,03 |
0,3 |
0,038 |
0 |
|
0 |
![]()
Wyszukiwarka