Politechnika Wrocławska
Wydział Geoinżynierii, Górnictwa i Geologii
Badania skał w trójosiowym stanie naprężenia
Wykorzystanie wyników badań do określenia parametrów kryteriów wytrzymałościowych:
- Kryterium Coulomba - Mohra
- Kryterium Hoeka - Browna
Prowadzący: Dr inż. A. Wojtaszek |
Wykonali:
Justyna Serwik Krzysztof Zimniak Wojciech Berhel |
Wrocław, 16.05.2005r.
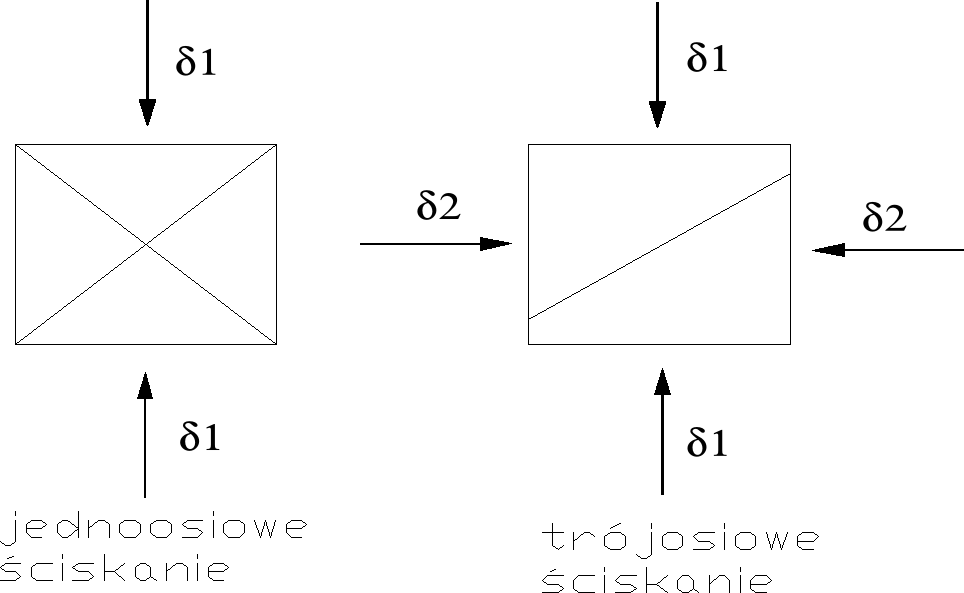
Złożoność warunków i stanów obciążeń skal zalegających w masywie wymaga badania ich właściwości mechanicznych nie w jednoosiowym, lecz w trójosiowym stanie naprężeń. Przeprowadzenie takich badań jest możliwe w laboratorium, przy zastosowaniu specjalnych urządzeń ciśnieniowych pozwalających na modelowanie stanu naprężeń zbliżonych do naprężeń naturalnych. Zróżnicowanie składowych stanu naprężenia osiąga się poddając próbkę skalną działaniu wszechstronnego ciśnienia. Stosuje się wiec zasadę Karmana, według której na jednoosiowy stan naprężenia nakłada się hydrostatyczny stan ciśnień ( σ1 > σ2 = σ3 ). Badania przeprowadza się na próbkach walcowych dla których większe naprężenie główne σ1 jest przykładane zgodnie z osią pionowa próbki, natomiast mniejsze naprężenie główne σ2 = σ3 oddziaływuje po obwodzie próbki w kierunku radialnym.
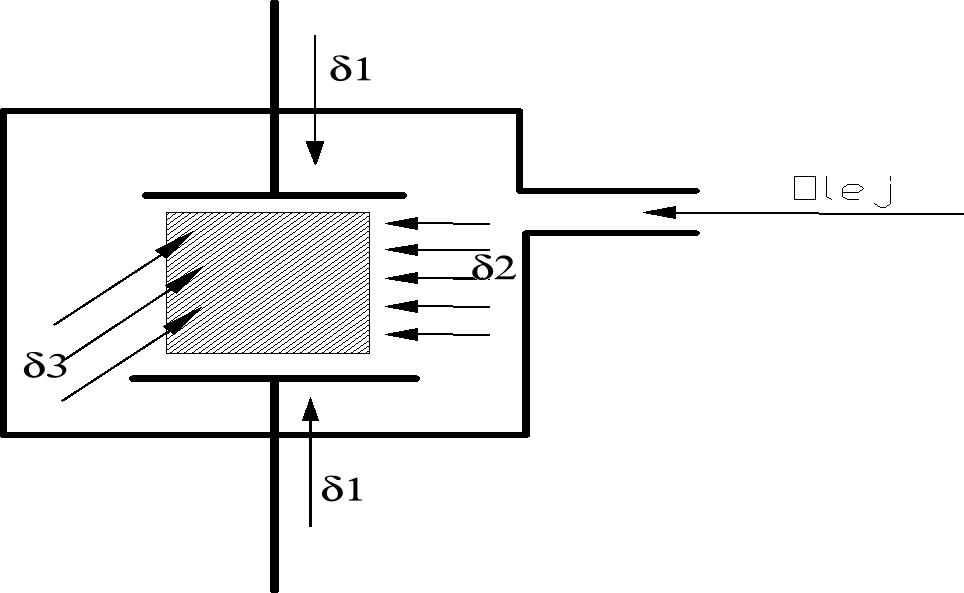
Badanie przeprowadza się w komorze Karmana, w której realizowany jest osiowo - symetryczny stan naprężenia. Ciśnienie boczne jest wywierane przez olej, natomiast obciążenie pionowe można uzyskać w sposób mechaniczny przy użyciu prasy hydraulicznej. Odpowiednio spreparowaną próbkę umieszcza się w specjalnej osłonie gumowej, która chroni próbkę przed dostępem oleju do próbki. Całość umieszcza się w komorze. Próbka ma średnicę 40 mm i smukłość równą 1. W celu odwzorowania stanu naprężeń, jaki panuje w górotworze stosuje się ciśnienia w zakresie 100MN/m2 dla ciśnienia pionowego. Stosowanie tak dużych ciśnień bocznych wywieranych przez olej na próbkę wymaga opracowania specjalnych rodzajów uszczelnień w systemie hydraulicznym oraz w komorze badawczej.
Typowe badanie skal w aparacie trójosiowego ściskania polega na określaniu wytrzymałości trzech próbek pochodzących z tej samej próbki pierwotnej, przy rożnych ciśnieniach bocznych. Na ogol przyjmuje się następujące stopnie ciśnienia bocznego: 20, 40, 60 MN/m2.
Rys. Komora Karmana.
Zniszczenie próbek poddanych wszechstronnemu ciśnieniu następuje powoli, przy jednoczesnym wzroście ciśnienia w układzie hydraulicznym i spadku obciążenia pionowego. W warunkach jednoosiowego ściskania próbki rozpadają się zazwyczaj na drobne odłamki, a w niektórych przypadkach występują dwa stożki okruchowe.
Natomiast w stanie trójosiowego ściskania zniszczenie próbek jednoosiowych następuje wzdłuż powierzchni zorientowanych ukośnie do podstawy. Charakterystyczne jest pojawienie się na powierzchni bocznych poziomych pęknięć, równoległych do podstaw.
Sposoby przeprowadzania doświadczeń w komorze Karmana :
klasyczny: wkładamy badaną próbkę do komory, i ustalamy ciśnienie boczne oleju na poziomie 20MPa. Następnie przystępujemy do ściskania próbki za pomocą tłoków aż do zniszczenia skały. Podobnie robimy przy ciśnieniach 40 i 60MPa.
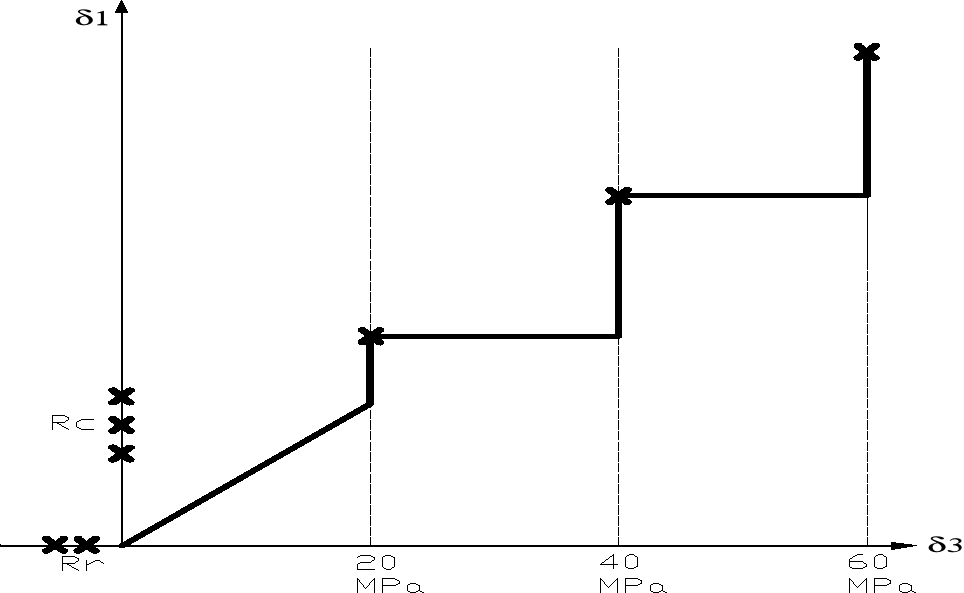
wielokrotnego zniszczenia: przy wielokrotnym zniszczeniu próbka musi zostać „opasana” czujnikami (tensometrami), które mierzą odkształcenie. Po włożeniu próbki do komory komputer ustala ciśnienie boczne na 20MPa i załącza tłoki ściskające skałę. Czujniki które są umieszczone na skale wskażą komputerowi w którym momencie ma przestać ściskać próbkę skały (tuż przed zniszczeniem). Następnie zostaje ustalone ciśnienie boczne na poziomie 40MPa i znowu zostają załączone tłoki, które tak samo jak poprzednio przestaną ściskać tuż przed zniszczeniem próbki. Czynności te zostają powtórzone przy ciśnieniu 60MPa.
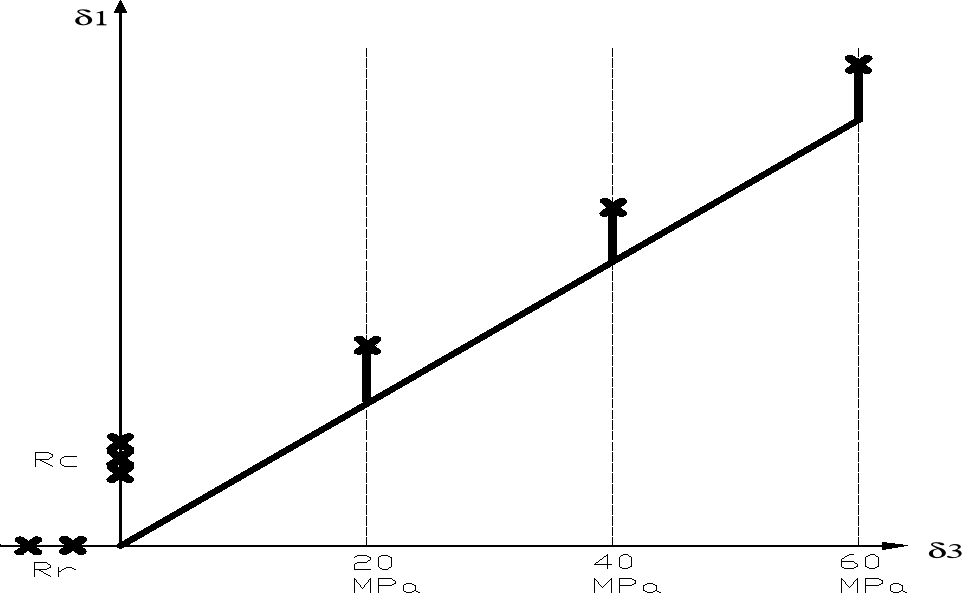
ciągłego zniszczenia: przy przeprowadzaniu doświadczenia metodą ciągłego zniszczenia próbka również zostaje oklejona czujnikami które rejestrują zmianę odkształcenia. W tym przypadku ponownie ustalamy ciśnienie boczne na poziomie 20MPa, a następnie wraz ze wzrostem ciśnienia jednocześnie ściska się próbkę.
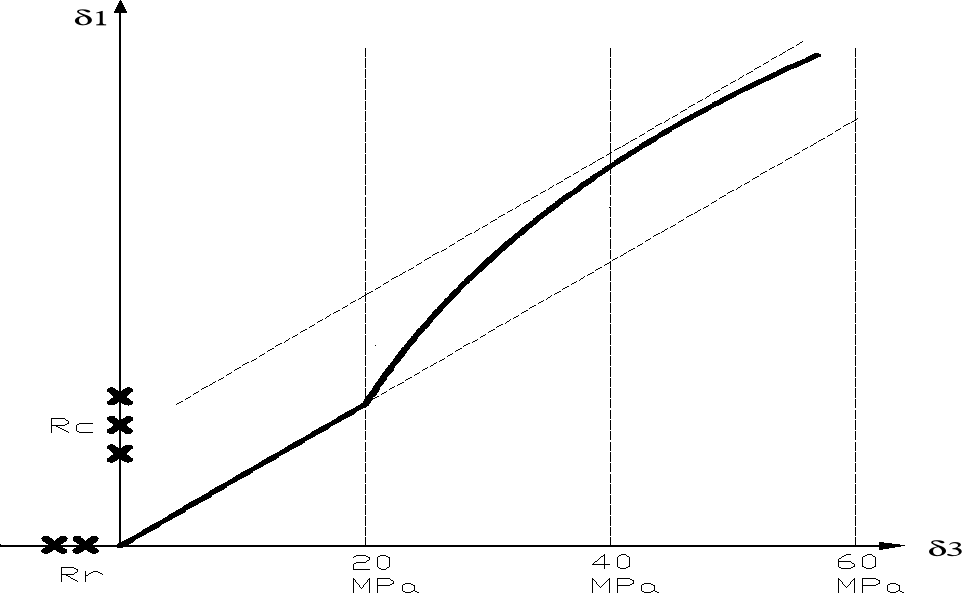
Opracowanie wyników przy użyciu kryterium Coulomba-Mohra polega na wykreśleniu obwiedni granicznych kół naprężeń reprezentujących ciśnienia wywierane przez próbkę w poszczególnych etapach badania, przy zadanym ciśnieniu bocznym.
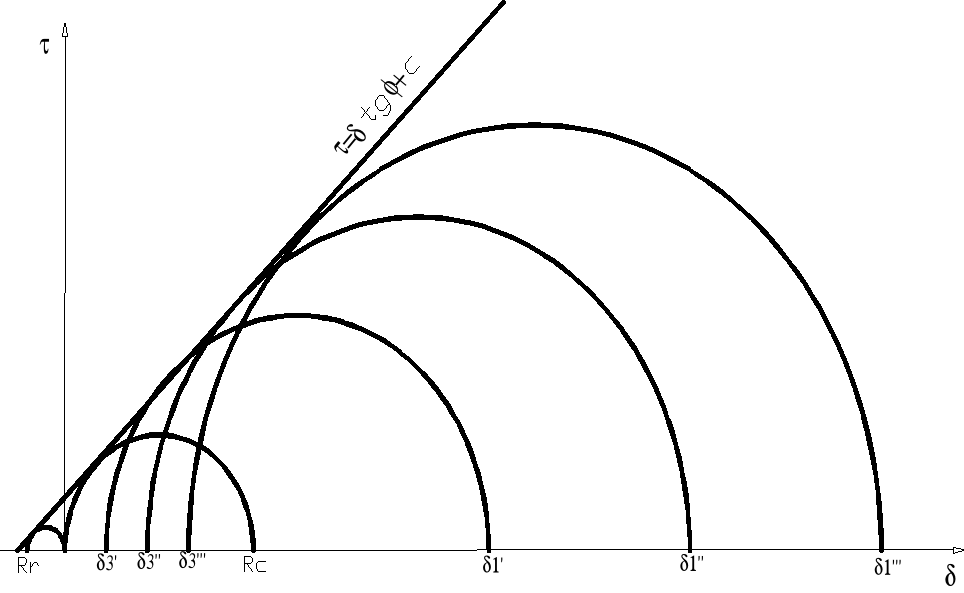
Rys. Teoretyczny przebieg obwiedni wytrzymałościowej
W tym celu nanosi się w układzie współrzędnych σ - τ poszczególne wartości i wykreśla się styczna, która jest w najprostszym przypadku linia prostą opisaną równaniem:
τ = σ tg ϕ + c
τ - naprężenie ścinające (styczne) [MPa]
σ - naprężenie normalne [MPa]
ϕ - kat tarcia wewnętrznego [o]
c - kohezja (spójność) [MPa]
Rzeczywisty przebieg obwiedni wytrzymałościowej ilustruje poniższy rysunek:
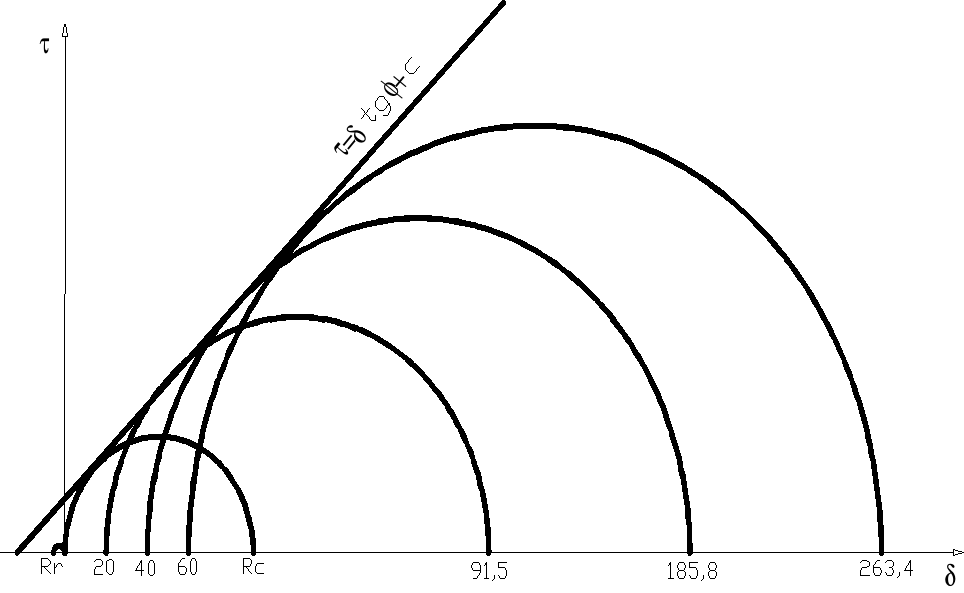
Jak widać na powyższym rysunku wytrzymałość skały na rozciąganie Rr jest bardzo mała przez co nie można poprowadzić prostej stycznej do wszystkich kół Mohra. Dlatego prosta styczna
τ = σ tg ϕ + c
została podzielona na dwie: dla kół jednoosiowego ściskania (Rr i Rc) oraz dla kół Rc i trójosiowego ściskania. Przez co w wynikach obliczeń otrzymamy dwa parametry c oraz dwa kąty ϕ które są odpowiedzialne za zniszczenie.
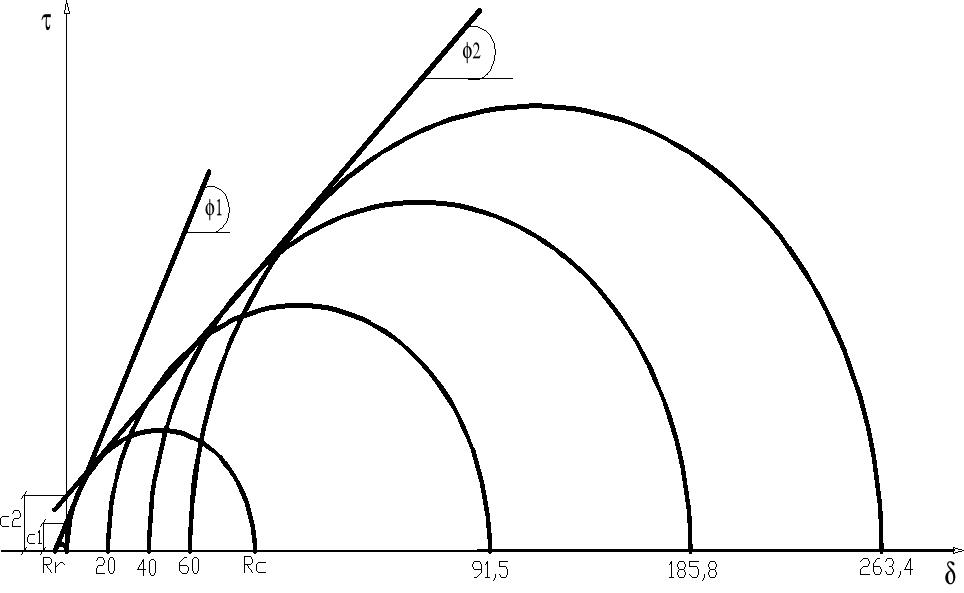
Aby było możliwe zastosowanie kryterium Coulomba-Mohra należy przejść do postaci
σ1 = f (σ3)
Wyprowadzenie wzoru:
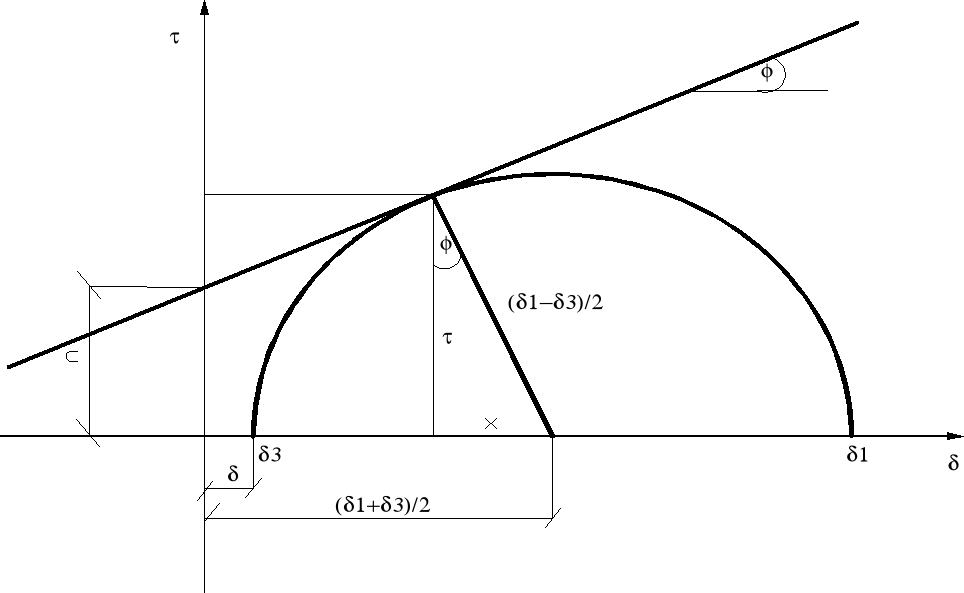
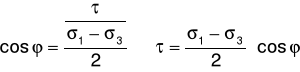
- styczne
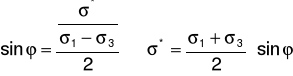
- normalne
![]()
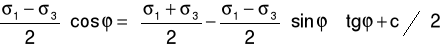
![]()
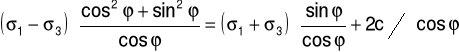
![]()
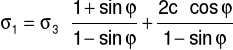
Następnie wprowadzając dane do komputera, przy użyciu arkusza kalkulacyjnego Excel, określiliśmy metodą najmniejszych kwadratów równanie prostej y = ax + b, odpowiadające w/w równaniu/
Dzięki temu z wzoru
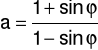
wyliczony został kąt tarcia wewnętrznego ϕ.
Natomiast spójność c obliczamy na podstawie wzoru
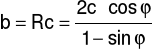
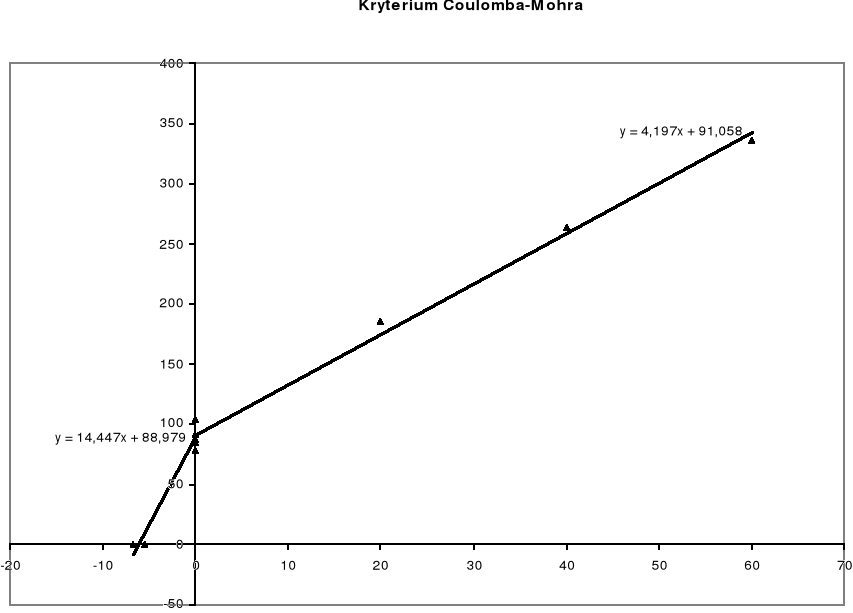
Kryterium Coulomba - Mohra
Dane wejściowe
Skała - piaskowiec drobnoziarnisty
Rr = 6,7 Mpa Rr = 5,5 Mpa
Rc = 78,7 MPa Rc = 91,5 MPa Rc = 87,8 MPa Rc = 104,3 MPa Rc = 84,3 MPa
|
Wyniki badań w komorze trójosiowej:
σ3 |
σ1 |
20 |
185,8 |
40 |
263,4 |
60 |
336,3 |
Parametry jednoosiowego stanu naprężeń:
Po aproksymacji prostej w układzie Rc - Rr otrzymujemy równanie postaci y = ax + b, gdzie:
a = 14,447
b = 88,979.
Równanie ma wówczas postać: y = 14,447x + 88,979.
Równanie to odpowiada równaniu:
![]()
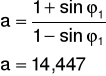
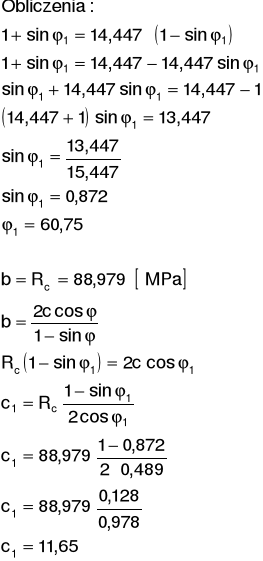
![]()
Parametry trójosiowego stanu naprężeń:
Po aproksymacji prostej w układzie σ1 - σ3 otrzymujemy równanie prostej postaci
y = ax + b
gdzie
a = 4,197
b = 91,058.
Równanie ma postać: y = 4,197x + 91,058.
Równanie to odpowiada równaniu:
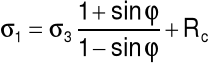
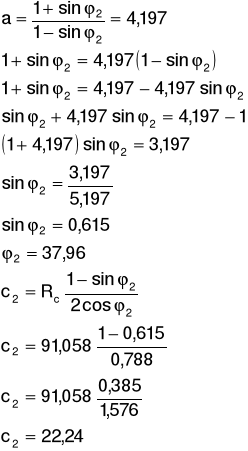
Zestawienie wyników obliczeń w tabeli:
σ3 [MPa] |
σ1 [MPa] |
ϕ1 [°] |
c1 [MPa] |
ϕ2 [°] |
c2 [MPa] |
Rc [MPa] |
20 |
185,8 |
60,75 |
11,65 |
37,96 |
22,24 |
88,979 |
40 |
263,4 |
|
|
|
|
|
60 |
336,3 |
|
|
|
|
|
Kryterium Hoeka - Browna
σ3 [MPa] |
σ1 [MPa] |
|
-6,7 |
0 |
44,89 |
-5,5 |
0 |
30,25 |
0 |
78,7 |
6193,69 |
0 |
91,5 |
8372,25 |
0 |
87,8 |
7708,84 |
0 |
104,3 |
10878,49 |
0 |
84,3 |
7106,49 |
20 |
185,8 |
27489,64 |
40 |
263,4 |
49907,56 |
60 |
336,3 |
76341,69 |
Po wprowadzeniu danych do arkusza kalkulacyjnego Excel określiliśmy metodą najmniejszych kwadratów równanie prostej y = ax + b, które odpowiada równaniu:
Współczynnikiem kierunkowym prostej jest .
Równanie prostej:
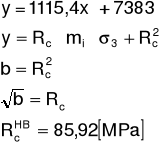
Określenie parametru mi:
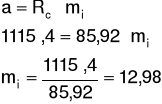
Stąd równanie:
![]()
Ma końcową postać:
![]()
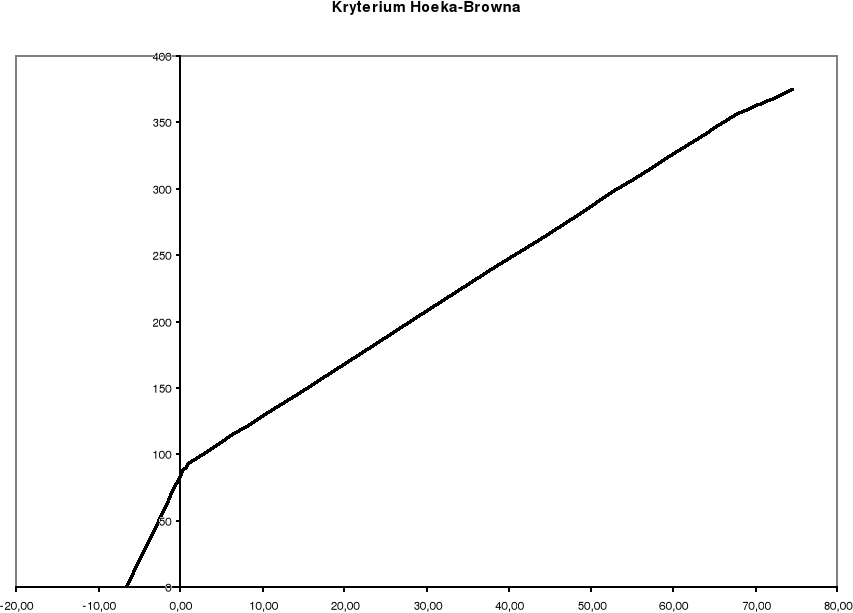
Po połączeniu obu kryteriów (Coulomba-Mohra i Hoeka-Browna) Uzyskano następujący wykres:
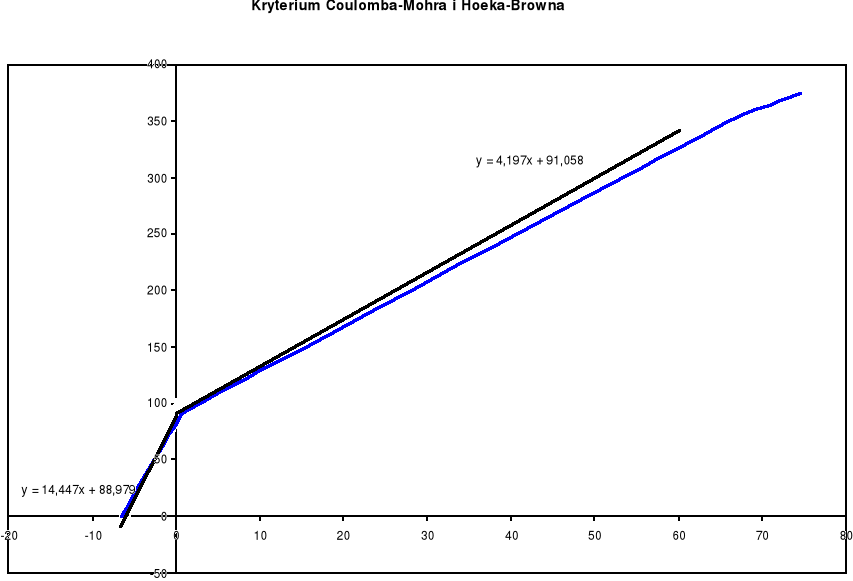
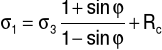
Wyszukiwarka