Moment siły względem punktu
Momentem siły względem punktu ( nazwanego punktem „O” ) nazywamy wektor momentu ![]()
O równy iloczynowi wektorowemu promienia ![]()
wyprowadzonego z punktu O do wektora ![]()
i wektora siły ![]()
. ![]()
O ![]()
=![]()
![]()
![]()
![]()
![]()
Jego kierunek ( ![]()
O ) jest prostopadły do płaszczyzny utworzonej przez wektory ![]()
i ![]()
. Jego wartość jest równa ![]()
=Fd. Zwrot ![]()
O zgodny z regułom śruby prawoskrętnej.
Składowe przyspieszenia punktu w naturalnym układzie współrzędnych
Przyspieszenie styczne ( powoduje zmianę modułu wektora prędkości, przyspieszenie styczne ma kierunek wektora predkości) at, przyspieszenie normalne( powoduje zmiane kierunku wektora predkosci i jest skierowane w strone środka krzywizny toru) an
Ruch złożony (parametry)
Ruchu złożony:
W zależności od układu odniesienia względem, którego badamy ruch mamy odczynienia z ruchem względnym i bezwzględnym.
Ruch ciała względem nieruchomego ciął w układzie odniesienia nazywamy ruchem bezwzględnym.
Ruch ciała względem ruchomego układu odniesienia nazywamy względny.
Ruch układu ruchomego względem nieruchomego ciała nazywamy ruchem unoszenia.
Prędkość w ruchu względnym{złożonym}:
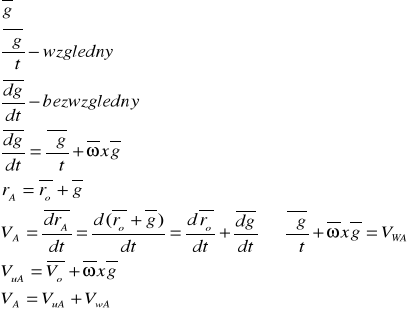
Przyspieszenie w ruchu złożonym:
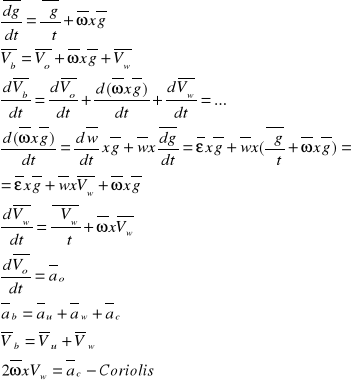
Zasada równowagi pracy i energii kinetycznej
Ek=L Energia kinetyczna punktu jest równa pracy jaką wykonał punkt aby przebić drogę s
Dynamiczne równania ruchu płaskiego 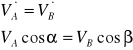
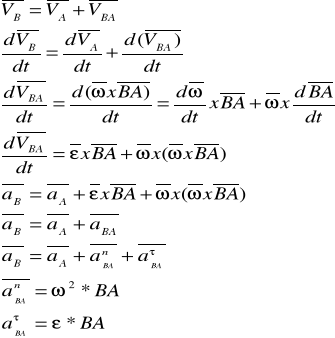
Prawa Newtona
I Prawo Newtona. Jeżeli na ciało nie działają żadne siły lub działające siły równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym po lini prostej.
II Prawo Newtona. Jeżeli na ciało działa siła ( wypadkowa wszystkich sil działających na punkt materialny jest różna od zera ), to porusza się ono względem inercjalnego układu odniesienia ruchem zmiennym z przyspieszeniem wprost proporcjonalnym do siły, a odwrotnie proporcjonalnym do masy ciała. Kierunek i zwrot wektora przyspieszenia są zgodne z kierunkiem i zwrotem wektora siły.
![]()
![]()
III Prawo Newtona. Jeżeli dwa ciała A i B działają wzajemnie na siebie, to siła ![]()
AB, z jaką ciało A działa na ciało B i siła ![]()
BA, z jaką ciało B działa na ciało A, są równe co do wartości, mają ten sam kierunek, ale przeciwne zwroty.
![]()
AB= -![]()
BA
Prawo Grawitacji Newtona. Każde dwa punkty materialne przyciągają się wzajemnie siłą wprost proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu odległości między nimi.
![]()
12=g![]()
![]()
- wektor jednostkowy, g - stała grawitacji
dynamiczne równania ruchu pkt materialnego
zasada D'Alemberta
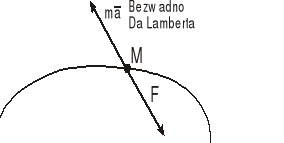
Na punkt materialny M działają siły rzeczywiste, które w każdej chwili równoważą się z siłą bezwładności tego punktu, tzw. Siłą Da Lamberta.
![]()
![]()
Siłą bezwładności ( lub siłą Da Lamberta ) nazywamy fikcyjną siłę ![]()
równą co do wartości iloczynowi masy i przyspieszenia punktu materialnego lecz przeciwnie do tego przyspieszenia skierowana.
W układzie Kartezjańskim: ![]()
Z równania ![]()
wynikają następujące równania różniczkowe: ![]()
Przykład. Punkt materialny o masie m wyrzucony jest z prędkością początkową v0 pod kątem α do poziomu - wyznacz wysokość i zasięg rzutu.
Ped masy, kręt
Pęd iloczyn masy ciała i jego predkosci p=mV
Praca mechaniczna
jest to iloczyn siły i odległosci przebytej przez punkt położenia tej siły w kierunku jej działania
L=F*s ; L=M*φ
Energia kinetyczna, zasada równowartosci pracy i energi kinetycznej
Energia kinetyczna jest energią ruchu definiowaną jako pracę jaką wykonuje poruszające się ciało,zanim zostanie doprowadone do spoczynku Ek= mV2/2, Ek=L
potencjalne pole sił, energia potencjalna
Energia potencjalna to energia zmagazynowana w ciele lub układzie wskutek jego położenia, kształtu lub stanu
zasda zachowania energii Ec=Ek+Ep
zasada ruchu srodka masy
Pochodna pędu jest równa sunie sil się wewnętrznych działających na układ w danym czasie.
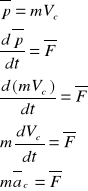
Środek masy punktów porusza się tak jakby w nim skąpione były wszystkie siły działające na układ punktów.
zasada zachowania pędu, i kretu
Pęd uk. Punktów materialnych jest równy iloczynowi masy wszystkich punktów i prędkości środka masy układu punktów materialnych.
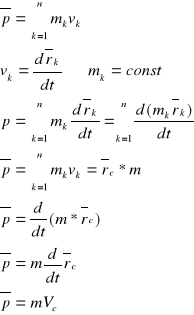
moment bezwladnosci < moemnty dewiacji
Momentem bezwładności ciała względem osi nazywamy granice, do której dąży suma iloczynów mas i kwadratów odległości od danej osi.
Moment bezwładności względem osi jest równy sumie momentów bezwładności względem dwóch wzajemnie prostopadłych płaszczyzn przecinających się wzdłuż tych osi, natomiast biegunowy moment bezwładności równy jest sumie momentów bezwładności względem trzech wzajemnie prostopadłych płaszczyzn przecinających się w biegunie albo połowie sumy momentów bezwładności względem trzech prostopadłych do siebie osi poprowadzonych z bieguna.
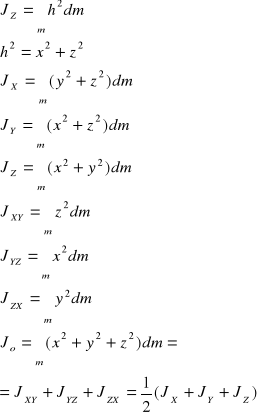
Momenty dywinacji
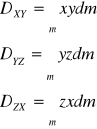
energia kinetyczna w ruchu postepowym i obrotowym
Ek=mV2/2 ; Ek=Iω2/2
twierdzenie Koeniga
ruch postepowy
Ruch postępowy ciała sztywnego:
Równolegle przesuniecie ciała sztywnego względem układu odniesienia nazywamy ruchem postepowym. Każdy punkt wykonuje przesuniecie równolegle zwane translacja.
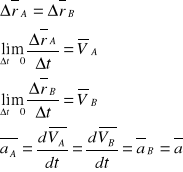
Wyszukiwarka