Badania operacyjne - to naukowa metoda rozwiązywania problemów z zakresu podejmowania decyzji kierowniczych.

Obszar wiedzy wykorzystywany w badaniach operacyjnych to spora część zakropkowanego obszaru na poniższym rysunku.

Pole zastosowań badań operacyjnych obejmuje sporządzanie matematycznych, ekonomicznych i statystycznych opisów (modeli) procesów decyzyjnych charakteryzujących się dużą złożonością (i często niepewnością). Takie opisy (modele) umożliwiają precyzyjne analizowanie złożonych procesów decyzyjnych i ułatwiają podejmowanie najlepszej decyzji.

Podstawowym narzędziem badań operacyjnych jest model.
Model (tutaj) jest to równanie (lub układ równań) za pomocą którego odzwierciedlamy procesy decyzyjne i społeczno-gospodarcze zachodzące w życiu gospodarczym.

Procesy decyzyjne dzielimy je na 4 podstawowe klasy. Podział jest ściśle związany z ilością i jakością informacji jaką dysponuje decydent w procesie podejmowania decyzji. Mówimy o podejmowaniu decyzji w warunkach:

1. pewności. Ma to miejsce wówczas, gdy każdej decyzji odpowiada jeden tylko wynik z prawdopodobieństwem równym jedności (mówimy, że proces jest zdeterminowany).

2. niepewności. Ma to miejsce wówczas, gdy każdej decyzji odpowiada więcej niż jeden wynik (mówimy, że proces jest procesem stochastycznym). Nie znamy jednak prawdopodobieństwa z jakim dany wynik może wystąpić.

3. ryzyka. Ma to miejsce wówczas, gdy każdej decyzji odpowiada więcej niż jeden wynik, ale znamy prawdopodobieństwo z jakim dany wynik może wystąpić.

4. częściowej informacji. Ma to miejsce wówczas, gdy każdej decyzji odpowiada więcej niż jeden wynik Nie znamy co prawda prawdopodobieństwa z jakim dany wynik może wystąpić, ale możemy próbować je oszacować dzięki znajomości niektórych charakterystyk nieznanego rozkładu prawdopodobieństwa, np. wartość oczekiwana, wariancja, mediana, dominanta, itp.

Elementy teorii decyzji - gry z naturą

	reakcja rynku (natury)
decyzja firmy	wysoka akceptacja	niska akceptacja
- duży system	200	20
- średni system	150	20
- mały system	100	60

Mamy do czynienia ze swoistą grą. W grze tej bierze udział dwóch graczy:

1. decydent (firma ), która ma trzy możliwości

2. natura (rynek usług), która ma dwie możliwości

"Przeciwnik" decydenta (rynek, natura) nie jest zainteresowany wynikiem gry.

Podstawowe sposoby analizowania gry z naturą oparte są na

1. analizie macierzy wypłat (macierzy korzyści lub macierzy strat) oraz

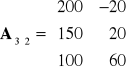
2. analizie drzewa decyzyjnego

Podejmowanie decyzji w warunkach niepewności

1. kryterium MaxiMax (skrajne postępowanie ryzykanta, optymisty)

2. kryterium MaxiMin (skrajne postępowanie asekuranta, pesymisty)

3. kryterium Hurwicza (postępowanie wypośrodkowane pomiędzy postępowaniem ryzykanta i asekuranta)

4. kryterium Savage'a (postępowanie minimalizujące straty z tytułu źle podjętej decyzji; kryterium to jest nazywane również kryterium MiniMax żalu lub kryterium MiniMax dogodnej straty)

5. kryterium Laplace'a (postępowanie maksymalizujące oczekiwany zysk; wszystkie stany natury są jednakowo prawdopodobne)

Kryterium MaxiMax

Należy wybrać taką decyzję
, że

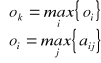
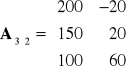
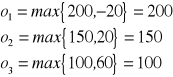
Kryterium MaxiMin

Należy wybrać taką decyzję
, że

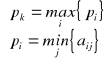
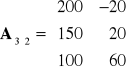
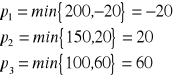
Kryterium Hurwicza

Niech
oznacza skłonność do ryzyka przy decyzji

. Należy wybrać taką decyzję
, że

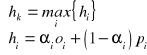
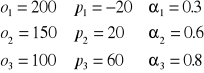
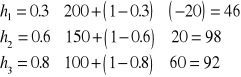
Kryterium Savage'a (MiniMax "żalu")

W pierwszym kroku należy zbudować macierz "żalu"

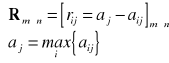
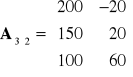
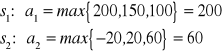
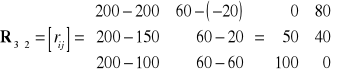
Należy wybrać taką decyzję
, że

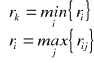
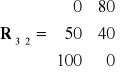
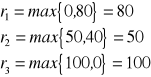
Kryterium Laplace'a

Przyjmuje się tutaj, że prawdopodobieństwo zaistnienia każdego z n stanów natury jest jednakowe i wynosi

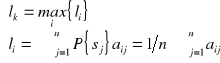
Należy wybrać taką decyzję
, że

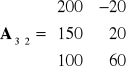
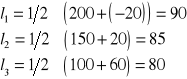
Podejmowanie decyzji w warunkach ryzyka

Dla każdego stanu natury
(
) określone jest prawdopodobieństwo zaistnienia tego stanu i wynosi
. Prawdopodobieństwa te noszą nazwę prawdopodobieństw a priori.

oraz

Działając w warunkach niepewności możemy posłużyć się następującymi kryteriami wyboru decyzji:

1. kryterium maksymalnej oczekiwanej wartości (MOW) zysku

2. kryterium minimalnego oczekiwanego "żalu"

Kryterium maksymalnej oczekiwanej wartości (MOW)

Należy wybrać taką decyzję
, że

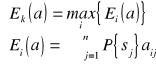
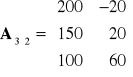
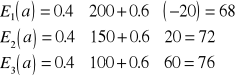
Kryterium minimalnego oczekiwanego "żalu"

Należy wybrać taką decyzję
, że

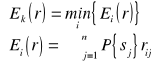
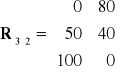
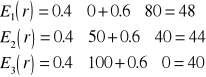
Cena graniczna doskonałej informacji

Cena graniczna doskonałej (perfekcyjnej) informacji jest to maksymalna kwota jaką warto zainwestować w dodatkowe badanie związane z poznaniem przyszłego zachowania się natury (rynku).

Doskonałą (perfekcyjną) informację definiujemy jako wiedzę
o przyszłym stanie natury przed podjęciem decyzji.

Można zadać sobie pytanie jaką korzyść osiągnęlibyśmy w warunkach doskonałej informacji? Wielkość tą nazwiemy oczekiwaną korzyścią w warunkach doskonałej (perfekcyjnej) informacji (OKPI).

oraz

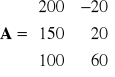
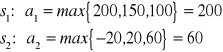
Cena graniczna doskonałej informacji (CGPI) wynika z porównania korzyści osiąganej w warunkach doskonałej informacji z korzyścią osiąganą w warunkach "normalnych" tj. w warunkach kiedy decyzja musi być podjęta przed zarejestrowaniem stanu natury.

Stanowi to różnicę pomiędzy kwotą OKPI i kwotą MOW.

Otrzymaną kwotę możemy interpretować jako maksymalną cenę, którą bylibyśmy skłonni zaakceptować za dodatkowe badanie rynku w celu zyskania większej pewności w zakresie reakcji rynku na proponowane usługi.

Zauważmy, że otrzymana kwota jest równa minimalnemu oczekiwanemu "żalowi"
, tj.

Cena graniczna doskonałej informacji jest równa minimalnemu oczekiwanemu "żalowi"

Podejmowanie decyzji z wykorzystaniem dodatkowej informacji

Załóżmy, że na zaistnienie stanu natury (rynku)
ma istotny wpływ K czynników (wskaźników)
. Celem analizy Bayesowskiej jest poznanie prawdopodobieństw warunkowych
, tj. prawdopodobieństw zaistnienia stanu natury
pod warunkiem, że wystąpił czynnik
(
). Prawdopodobieństwa
nazywane są w analizach problemów decyzyjnych prawdopodobieństwami a posteriori i są zrewidowaną formą prawdopodobieństw a priori
.

Najczęściej mamy do czynienia z sytuacją kiedy w wyniku dodatkowych badań (eksperymentów) oszacowano prawdopodobieństwa warunkowe

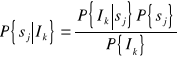
gdzie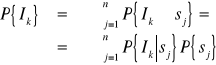

zainteresowanie	stan rynku
konkurencyjnych firm	duży popyt	niski popyt
- minimalne	10%	50%
- umiarkowane	40%	30%
- znaczne	50%	20%

oraz

	0.1	0.5
	0.4	0.3
	0.5	0.2

	0.4	0.1	0.40.1=0.04	0.040.34=0.1176
	0.6	0.5	0.60.5=0.30	0.300.34=0.8824
	1.0		=0.34	1.0000

	0.4	0.4	0.40.4=0.16	0.160.34=0.4706
	0.6	0.3	0.60.3=0.18	0.180.34=0.5294
	1.0		=0.34	1.0000

	0.4	0.5	0.40.5=0.20	0.040.32=0.6250
	0.6	0.2	0.60.2=0.12	0.300.32=0.3750
	1.0		=0.32	1.0000

W zależności od "zachowania się" wskaźnika
decyzjami optymalnymi będą:

1. d3 jeżeli wystąpi wskaźnik I1 (niewielkie zainteresowanie konkurencji) ponieważ

2. d1 jeżeli wystąpi wskaźnik I2 (umiarkowane zainteresowanie konkurencji) ponieważ

3. d1 jeżeli wystąpi wskaźnik I3 (znaczne zainteresowanie konkurencji) ponieważ

Oczekiwaną korzyść osiąganą przy dodatkowej informacji (OKDI) definiujemy jako

Różnicę pomiędzy oczekiwaną korzyścią przy uwzględnieniu dodatkowej informacji (OKDI), a oczekiwaną korzyścią bez uwzględnienia dodatkowej informacji (MOW) nazywamy oczekiwaną wartością dodatkowej informacji (OWDI).

Efektywność dodatkowej informacji (EDI) definiujemy jako stosunek oczekiwanej wartości dodatkowej informacji (OWDI) do ceny granicznej doskonałej informacji (CGPI)

1

Dorota Miszczyńska, Marek Miszczyński, KBO UŁ, Elementy teorii decyzji

---