Podstawowy wzór teorii kinetycznej gazu.
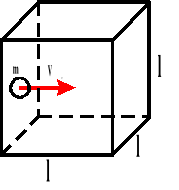
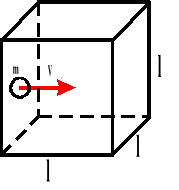
W zbiorniku znajduje się „n” cząsteczek gazu. Bierzemy jedną cząsteczkę, która porusza się od ściany do ściany i z powrotem.
Przyrost pędu wynosi:
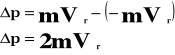
Przyrost pędu jest równy udzielonemu popędowi:
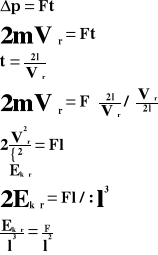
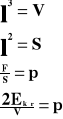
Powyższy wzór przedstawia ciśnienie, jakie wywiera jedna cząsteczka gazu na ścianki naczynia.
Ponieważ w naczyniu znajduje się „n” cząsteczek gazu, a sześcian ma trzy pary ścian, to ciśnienie jakie wywiera gaz na ścianki naczynia wynosi:
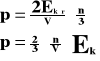
l - wymiar sześcianu
m - masa gazu
p - ciśnienie
V - prędkość
F - siła
Ek - energia kinetyczna
n - ilość cząsteczek
Parametry określające stan fizyczny gazu.
Aby rozwiązać wszystkie problemy fizyczne związane z gazem, należy znać jego parametry, którymi są:
ciśnienie - p
temperatura - T
objętość -V
Związek temperatury z energią kinetyczną.
![]()
Stosunek energii kinetycznej gazu do jego temperatury jest wielkością stałą.
Ek - energia kinetyczna gazu
T - temperatura gazu
C - wielkość stała
Bezwzględna skala temperatur.
T[K] |
t[C] |
|
|
373,16 |
100 |
|
|
273,16 |
0 |
|
|
|
|
|
|
|
|
0 |
-273,16 |
|
|
Aby przejść ze skali Celsjusza na skalę Kalwina należy:
![]()
Aby przejść ze skali Kalwina na skalę Celsjusza należy:
![]()
Równanie gazu doskonałego.
Aby wyprowadzić równanie gazu doskonałego korzystamy z podstawowego wzoru teorii kinetycznej.
![]()
Z zależności energii kinetycznej gazu do jego temperatury bezwzględnej.
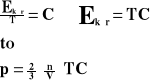
Przenosimy na lewą stronę wartości zmienne.
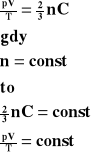
Dla stałej masy gazu stosunek iloczynu ciśnienia i objętości tego gazu do jego temperatury bezwzględnej jest wielkością stałą.
Ek - energia kinetyczna
n - ilość cząsteczek
V - objętość
T - temperatura bezwzględna
C - wielkość stała
p - ciśnienie
Równanie Clapeyrona.
Bierzemy jeden mol gazu w warunkach naturalnych.
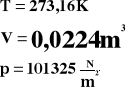
Powyższe wartości podstawiamy do równania gazu doskonałego.
![]()
Powyższa wartość została nazwana stałą gazową.
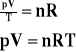
![]()
Czyli:
Powyższy wzór jest równaniem Clapeyrona.
Liczbę moli możemy obliczyć ze stosunku masy gazu do masy atomowej tego gazu.
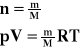
T - temperatura bezwzględna
V - objętość
p - ciśnienie
R - stała gazowa
n - ilość moli
M - masa atomowa
m - masa gazu
Przemiana izotermiczna.
Przemiana izotermiczna, to taka , w której wielkością stałą jest temperatura gazu, a zmiennymi są ciśnienie i objętość.
![]()
T - temperatura gazu
p - ciśnienie gazu
V - objętość gazu
Prawo Boyle'a-Mariotte'a
Przy
![]()
i
![]()
to
![]()
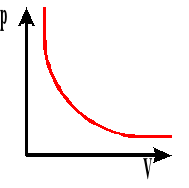
Przy stałej temperaturze, dla stałej masy gazu iloczyn ciśnienia i objętości jest wielkością stałą.
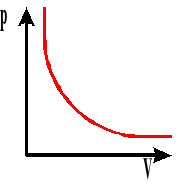
Izoterma gazu. Wykres zależności ciśnienia od objętości przy stałej temperaturze.
T - temperatura gazu
p - ciśnienie gazu
V - objętość gazu
m - masa gazu
Przemiana izobaryczna.
![]()
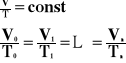
Przemiana izobaryczna, to taka przemiana, w której wielkością stałą jest ciśnienie, a objętość i temperatura są zmienne.
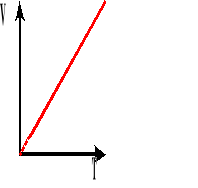
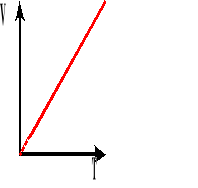
Wykres zależności objętości od temperatury, przy stałym ciśnieniu.
![]()
Współczynnik rozszerzalności objętościowej jest to względny przyrost objętości, przypadający na jednostkowy przyrost temperatury.
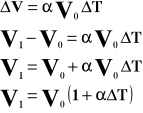
Powyższy wzór przedstawia objętość gazu po podgrzaniu go od T stopni.
- współczynnik rozszerzalności objętościowej
V - objętość gazu
T - temperatura gazu
p - ciśnienie gazu
Przemiana izochoryczna.
![]()
Przemiana izochoryczna, to przemiana, w której wielkością stałą jest objętość, a temperatura i ciśnienie zmieniają się.
V - objętość gazu
T - temperatura gazu
p - ciśnienie gazu
Prawo Charlesa.
Przy
![]()
i
![]()
to
![]()
![]()
Przy stałej objętości, dla stałej masy gazu stosunek ciśnienia do temperatury bezwzględnej jest wielkością stałą.
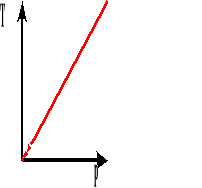
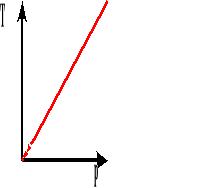
Wykres zależności ciśnienia od temperatury bezwzględnej przy stałej objętości.
![]()
Współczynnik rozprężliwości termicznej jest to względny przyrost ciśnienia przypadający na jednostkowy przyrost temperatury.
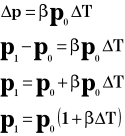
Powyższy wzór przedstawia wartość ciśnienia po podgrzaniu go o T stopni.
- współczynnik rozprężliwości termicznej
V - objętość gazu
T - temperatura gazu
p - ciśnienie gazu
m - masa gazu
Ciepło molowe.
Ciepłe molowym przy stałym ciśnieniu nazywamy taką ilość ciepła, która potrzebna jest do ogrzania jednego mola gazu o jeden stopień przy stałym ciśnieniu.
![]()
![]()
Ciepłe molowym przy stałej objętości nazywamy taką ilość ciepła, która potrzebna jest do ogrzania jednego mola gazu o jeden stopień przy stałej objętości.
Cp - ciepło molowe przy stałym ciśnieniu
CV - ciepło molowe przy stałej objętości
K - stała
Przemiana adiabatyczna.
Przemiana adiabatyczna jest to przemiana, w której zmienia się ciśnienie, objętość i temperatura, ale nie ma wymiany ciepła z otoczenia.
Równanie Poissona.
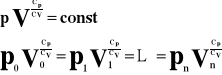
Lub:
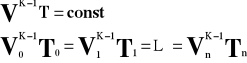
V - objętość gazu
T - temperatura gazu
p - ciśnienie gazu
Prawo Daltona.
![]()
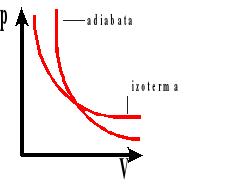
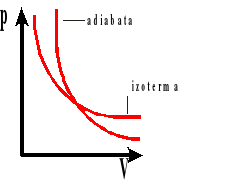
Wykres zależności ciśnienia od objętości dla przemian: adiabatycznej i izotermicznej.
P - ciśnienie gazu
V - objętość gazu
Właściwości sprężyste gazów, cieczy
i ciał stałych.
Wszystkie ciała posiadają sprężystość objętości, to znaczy, że po ustąpieniu siły powracają do swojej dawnej objętości.
Sprężystość postaci posiadają tylko ciała stałe, a ciecze i gazy przyjmują kształty pojemników, w których się znajdują.
Ciała stałe dzielimy na:
Sprężyste - które po ustąpieniu siły powracają do dawnej postaci;
Plastyczne - w wyniku działającej siły ulegają trwałym odkształceniom;
Kruche - w wyniku działającej siły ulegają zniszczeniu.
Prawo Hooke'a.
Prawo to dotyczy przyrostu długości, który następuje w wyniku działania sił wewnętrznych na ciało.
![]()
Przyrost długości rozciąganego pręta lub drutu zależy wprost proporcjonalnie od działającej siły i długości początkowej, a odwrotnie proporcjonalnie od przekroju poprzecznego powierzchni.
l - długość pręta lub drutu
F - działająca siła
S - pole przekroju poprzecznego
k - współczynnik proporcjonalności
Naprężenie wewnętrzne.
![]()
Naprężeniem wewnętrznym nazywamy stosunek siły działającej na ciało do pola przekroju poprzecznego rozciągniętego druta lub pręta.
F - działająca siła
S - pole przekroju poprzecznego
p - naprężenie wewnętrzne
Moduł Younga.
![]()
Modułem Yanga nazywamy wartość naprężenia wewnętrznego, które odpowiada podwojeniu długości ciała.
E - moduł Yanga
K - współczynnik proporcjonalności
Granica sprężystości i wytrzymałości.
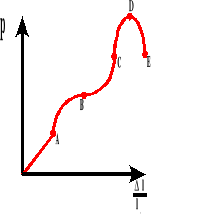
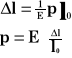
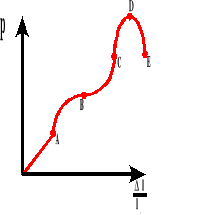
Wykres zależności wydłużenia względnego do naprężenia wewnętrznego.
A - granica proporcjonalności
B - granica sprężystości
B-C - obszar plastyczny
D - granica wytrzymałości
E - rozerwanie ciała
Wytrzymałością na rozerwanie nazywamy wartość naprężenia wewnętrznego, po której przekroczeniu następuje rozerwanie ciała.
L - długość pręta lub drutu
P - naprężenie wewnętrzne
E - moduł Yanga
Kryształy.
Wszystkie ciała możemy podzielić na krystaliczne i nie krystaliczne (bezpostaciowe).
Kryształ charakteryzują się regularną budową, w związku z tym można zbudować sieć krystaliczną. Najprostszą siec posiada sól kuchenna (sześcian). Kryształy charakteryzują się ściśle określoną temperaturę topnienia, a ciała bezpostaciowe mają pewne przedziały temperaturowe, w których to przechodzą w ciecz lub odwrotnie.
Kryształy możemy podzielić na:
monokryształy - powstają wokół jednego centrum krystalizacji;
polikryształy - powstają wokół wielu centrów krystalizacyjnych.
Siły między molekularne
(między cząsteczkowe).
Siły między molekularne są to siły wzajemnego oddziaływania między cząsteczkami.
Występujące siły to:
spójności - między cząsteczkami tego samego ciała;
przylegania - między cząsteczkami różnych ciał.
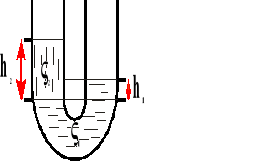
Włoskowatość.
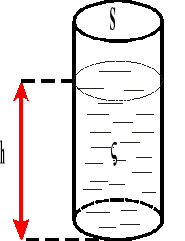
Włoskowatość jest to zjawisko kapilarne; zjawisko powstaje pod wpływem napięcia powierzchniowego; najpowszechniejszymi są zjawiska wciągania cieczy w wąskie rurki lub pory o ściankach zwilżonych przez wodę. W wyniku włoskowatości poziom cieczy w tych naczyniach może być wyższy, względnie niższy, niż wynika to z prawa naczyń połączonych.
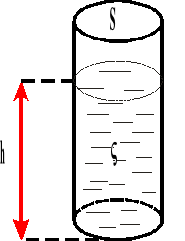
Wysokość słupka cieczy w tych naczyniach obliczamy ze wzoru:
![]()
h - wysokość
r - promień
g - przyspieszenie ziemskie
δ napięcie powierzchniowe
gęstość cieczy
Ciśnienie hydrostatyczne.
![]()
Ciśnienie wyraża się stosunkiem ciężaru ciała do powierzchni, na którą ono przypada.
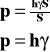
ale
![]()
to
![]()
p - ciśnienie hydrostatyczne
P - ciężar ciała
S - powierzchnia
h - wysokość
gęstość cieczy
γ ciężar właściwy cieczy
g - przyspieszenie ziemskie
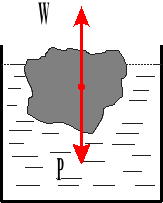
Prawo Archimedesa.
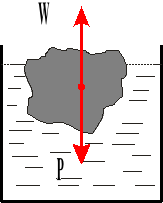
![]()
Na każde ciało zanurzone w ciecz działa siła wyporu skierowana pionowo do góry i równa ciężarowi cieczy wypartej przez to ciało.
W - siła wyporu
V - objętość
g - przyspieszenie ziemskie
c gęstość ciała
γc ciężar właściwy ciała
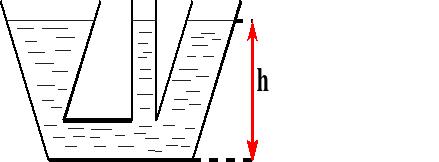
Naczynia połączone.
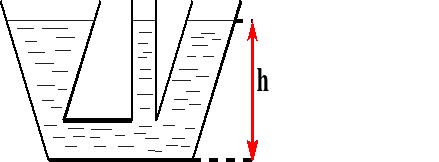
W naczyniach połączonych ciecz jednorodna (o tej samej gęstości) ustawia się na jednakowej wysokości.
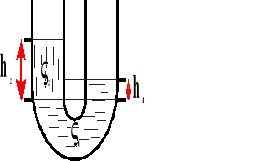
Na tej samej wysokości w naczyniach połączonych panuje taki samo ciśnienie.
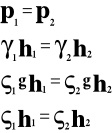
p - ciśnienie
h - wysokość
gęstość cieczy
γ ciężar właściwy cieczy
g - przyspieszenie ziemskie
Rozszerzalność liniowa ciał stałych.
![]()
Współczynnik rozszerzalności liniowej jest to względny przyrost długości przypadający na jednostkowy przyrost czasu.
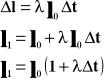
Powyższy wzór przedstawia długość ciała po podgrzaniu go o T stopni.
współczynnik rozszerzalności liniowej
T - temperatura
l - długość
Rozszerzalność objętościowa ciał stałych.
![]()
Współczynnik rozszerzalności objętościowej jest to względny przyrost objętości przypadający na jednostkowy przyrost temperatury.
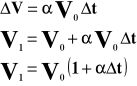
Powyższy wzór przedstawia objętość ciała po podgrzaniu go o T stopni.
współczynnik rozszerzalności objętościowej
T - temperatura
V - objętość
Gazy, ciecze i ciała stałe
Gazy, ciecze i ciała stałe
16
15
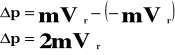
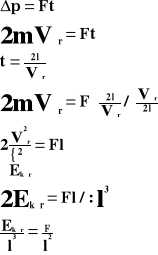
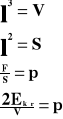
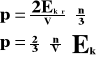
![]()
![]()
![]()
![]()
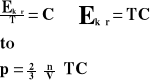
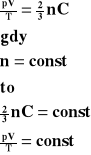
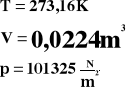
![]()
![]()
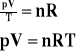
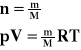
![]()
![]()
![]()
![]()
![]()
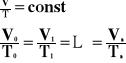
![]()
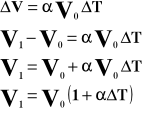
![]()
![]()
![]()
![]()
![]()
![]()
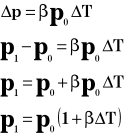
![]()
![]()
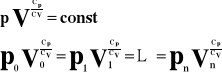
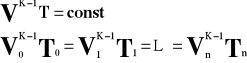
![]()
![]()
![]()
![]()
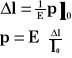
![]()
![]()
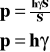
![]()
![]()
![]()
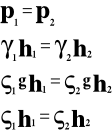
![]()
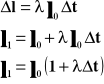
![]()
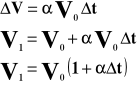
Wyszukiwarka