Prognozowanie i symulacje

dr A. Jankiewicz-Siwek

2003-02-20

Literatura:

„Prognozowanie gospodarcze - metody i zastosowania” pod red. M. Cieślak

„Teoria prognozy” Aleksander Zeliaś (prognoza na podstawie modelu ekonometrycznego)

„Prognozowanie gospodarcze” pod red. E. Nowaka

Prognozowanie to racjonalne, naukowe przewidywanie przyszłych zdarzeń.

Według prof. Czerwińskiego jest to sąd o zajściu określonego zdarzenia w czasie określonym z dokładnością do momentu lub okresu czasu należącego do przyszłości.

Według prof. Helwiga prognozowanie statystyczne jest to każdy sąd, którego prawdziwość jest zdarzeniem losowym przy czym prawdopodobieństwo tego zdarzenia jest znane i wystarczająco duże dla celów statystycznych (praktycznych).

Według prof. Cieślaka to sąd, który ma następujące własności:

• sformułowany jest z wykorzystaniem dorobku nauki;

• odnoszący się do określonej przyszłości;

• weryfikowany empirycznie;

• niepewny, ale akceptowany.

Założenia prognozowania (warunki klasyczne), które są dosyć sztywne:

1. znajomość modelu zmiennej prognozowanej:

• znajomość jego postaci analitycznej;

• znajomość ocen występujących w nim parametrów;

• znajomość ocen struktury stochastycznej modelu;

2. stabilność prawidłowości ekonomicznych w czasie - parametry dotyczące przeszłości i przyszłości powinny być takie same;

3. stabilność rozkładu składnika losowego modelu;

4. znane są wartości zmiennych objaśniających modelu w okresie prognozowanym;

5. dopuszczalna jest ekstrapolacja modelu poza zaobserwowany w próbie obszar zmienności zmiennych objaśniających.

Zmiany w prognozie polegają obecnie na zastąpieniu stabilności modelu prawie stabilnością. Przez prawie stabilność należy rozumieć sytuację, gdy parametry modelu ulegają zmianie, ale zmiany te są regularne oraz stosunkowo powolne.

Metody adaptacyjne - do ich stosowania nie trzeba stawiać żadnych założeń.

Podstawowe postulaty teorii predykcji:

• każda prognoza powinna być obliczona z odpowiednim miernikiem rzędu dokładności;

• przy wyborze sposobu budowy prognozy dążyć należy do możliwie wysokiej efektywności predykcji, tj. do osiągnięcia możliwie zadawalającej wartości wybranego miernika rzędu dokładności predykcji.

Funkcje prognoz:

• preparacyjna - prognozowanie jest działaniem, które przygotowuje inne działania;

• aktywizująca - polega na pobudzaniu do podejmowania działań sprzyjających realizacji prognozy, gdy zapowiada się zdarzenie korzystne i przeciwstawiających się realizacji, gdy zapowiada się zdarzenie niekorzystne;

• informacyjna - polega na zapoznaniu z nadchodzącymi zmianami.

Klasyfikacja prognoz:

1. ze względu na horyzont czasowy (podział względny):

1. krótkoterminowe - uważa się prognozę na taki przedział czasu, w którym zachodzą tylko zmiany ilościowe. Zwykle nie przekracza 1 roku;

2. średnioterminowe - dotyczą od 2 do 5 lat. Jest to okres czasu, w którym oczekuje się nie tylko zmian ilościowych, ale śladowych zmian jakościowych. Zmiany jakościowe polegają na zmianie istotnych cech zjawiska. Znajdują wyraz w odejściu od dotychczasowej prawidłowości, np. zmiana postaci trendu;

3. długoterminowe - obejmują ponad 5 lat, czyli dotyczą takiego przedziału czasu, w którym mogą wystąpić zarówno zmiany ilościowe, jak i poważne zmiany jakościowe;

4. perspektywiczne - horyzont czasowy od 10 do 20 lat.

2. ze względu na cel:

1. ostrzegawcze - zadaniem jest przewidywanie zdarzeń niekorzystnych dla odbiorców prognozy;

2. badawcze - mają na celu wszechstronne rozpoznanie przyszłości i ukazanie wielu możliwych ich wersji;

3. normatywne - podstawowym zadaniem jest ułatwienie wyboru potrzeb i przyszłych celów wraz z określeniem zadań i środków;

3. ze względu na funkcje:

1. operacyjne - są wykorzystywane jako narzędzie planowania operatywnego oraz bieżącej polityki gospodarczej. Obejmują stosunkowo krótkie okresy czasu, z reguły nie przekraczające 1 roku;

2. strategiczne - pełnią rolę narzędzi planowania długookresowego i perspektywicznego. Mają za zadanie stworzyć podstawy do podejmowania długofalowych decyzji gospodarczych;

4. ze względu na charakter prognozowanych zjawisk:

1. ilościowe - gdy stan zmiennej prognozowanej podany jest jedną liczbą, np. prognozowanie stóp procentowych. Dzielą się na:

• punktowe, które są liczbą uznaną za najlepszą ocenę zmiennej prognozowanej;

• przedziałowe, czyli przedział liczbowy, który z góry zadanym prawdopodobieństwem nazywanym wiarygodnością prognozy zawiera nieznaną wartość zmiennej prognozowanej w okresie prognozowanym;

2. jakościowe - dotyczą zjawisk typu jakościowego, np. prognozowanie kandydatów na prezydenta;

ze względu na szczegółowość danych:

1. ogólne;

2. szczegółowe;

ze względu na zasięg terytorialny:

1. światowe;

2. międzynarodowe;

3. krajowe;

4. regionalne;

5. lokalne;

ze względu na zakres ujęcia:

1. całościowe i częściowe;

2. globalne i odcinkowe;

3. kompleksowe i fragmentaryczne.

Zasady prognozowania (punktem wyjścia do tych zasad jest nasz stosunek do ważności informacji):

1. zasada status quo - oznacza, że prawidłowości zaobserwowane w przeszłości będą aktualne w przyszłości. Wszystkie informacje są jednakowo ważne i wszystkie są wykorzystywane w prognozowaniu;

2. zasada postarzania informacji - w miarę upływu czasu zmieniają się prawidłowości ekonomiczne. Dane starsze mają mniejsze znaczenie niż dane nowsze. Dlatego danym z różnych okresów przypisuje się różne rangi.

2003-02-27

Dane statystyczne wykorzystywane w prognozowaniu:

1. wewnętrzne - gromadzone są w obiekcie prognozowanym na potrzeby zarządzania tym obiektem lub specjalnie na potrzeby prognozowania;

2. zewnętrzne - zakres ich nie zależy od obiektu, dla którego sporządza się prognozę.

Inny podział danych:

1. statystyczne - prezentujące stan zjawisk i procesów w jednym momencie, w jednorodnych jednostkach czasu;

2. dynamiczne - prezentujące dynamikę zjawisk i procesów opracowane w formie szeregów czasowych;

3. przekrojowo-czasowe.

Horyzont prognozy - to przedział, w którym można sporządzać dopuszczalne prognozy badanego zjawiska.

Długość horyzontu prognozy zależy od:

• charakteru obiektu prognozy;

• wybranego modelu prognostycznego;

• zastosowanej metody prognozowania.

Reguła prognozowania to sposób przejścia od danych przetworzonych do prognozy. Wyróżniamy cztery reguły prognozowania:

1. reguła podstawowa - prognozą jest stan zmiennej prognozowanej w okresie T lub momencie otrzymany z modelu tej zmiennej przy przyjęciu założenia, że model ten będzie aktualny w chwili, na którą określa się prognozę. Może być stosowana, gdy prognosta jest przekonany, że model z przeszłości będzie aktualny również w przyszłości. Jest użyteczna, gdy prognozuje się zjawiska z powolnymi zmianami ilościowymi:

Y_T^* = E(Y_T) T>n

gdzie:

Y_T^* - prognoza zmiennej Y w momencie lub okresie T;

E(Y_T) - nadzieja matematyczna (wartość oczekiwana) zmiennej Y w momencie lub okresie T;

2. reguła podstawowa z poprawką - jest modyfikacją reguły podstawowej. Korzysta się z niej wówczas, gdy występuje uzasadnione przypuszczenie, że ostatnio zaobserwowane odchylenie wartości empirycznych od teoretycznych utrzymały się w przyszłości:

Y_T^* = E(Y_T) + p T>n

p = y_n -
- gdy zmiany dotyczą jednej chwili

p =

- gdy zmiany dotyczą kilku chwil

gdzie:

p - poprawka

3. reguła największego prawdopodobieństwa - prognozą jest tu wartość modalna rozkładu, co oznacza, że prognozą jest stan zmiennej, któremu odpowiada największe prawdopodobieństwo lub maksymalna wartość funkcji gęstości rozkładu:

Y_T^* = M_o(Y_T)

gdzie:

M_o - modalna

4. reguła minimalnej straty - to stan zmiennej, którego realizacja powoduje minimalne straty. Przyjmuje się, że wielkość straty jest funkcją błędu prognozy i poszukuje się minimum tej funkcji. Stosuje się ją w bardzo nielicznych przypadkach.

Metody prognozowania to sposób, który służy do rozwiązania zadań prognostycznych. Ze względu na rodzaj sporządzanej prognozy, jej cel, charakter przewidywanego zjawiska znajdują zastosowanie różne metody prognostyczne, które ogólnie dzielimy na:

1. metody matematyczno-statystyczne - wśród których wyróżniamy metody:

1. oparte na modelach deterministycznych;

2. oparte na modelach ekonometrycznych, które dzielimy na:

• jednorównaniowe modele ekonometryczne (klasyczna metoda trendu; adaptacyjne metody trendu; modele przyczynowo-skutkowe; modele autoregresyjne)

• wielorównaniowe modele ekonometryczne (modele proste; modele rekurencyjne; modele o równaniach współzależnych);

Wśród metod matematyczno-statystycznych główną rolę odgrywają metody oparte na modelach ekonometrycznych, które są statystycznym wyrazem praw ekonomii. Zmienne modelu i jego postać analityczną dobiera się według wskazań ekonomii, a parametry szacowane są na podstawie próby charakteryzującej wybrany fragment rzeczywistości.

2. metody niematematyczne (heurystyczne) - wśród których znajdują się metody: ankietowe; intuicyjne; ekspertyz; kolejnych przybliżeń; delficka; analogowa; modelowa; refleksji; inne. Heurystyczne metody prognozowania polegają na wykorzystaniu opinii ekspertów opartej na wiedzy, doświadczeniu, a często intuicji. Przewidywanie przyszłości nie jest ekstrapolowaniem wykrytych w przeszłości prawidłowości lecz prognozowaniem możliwych wariantów rozwoju interesujących nas zjawisk i wskazywaniem najbardziej prawdopodobnych czyli realistycznych. Wykorzystywane są do długookresowego prognozowania, np. nowych technologii czy odkryć naukowych.

Wybór metody prognozowania jest wspomagany przez ocenę jakości modelu, tj. ocenę jego zgodności z danymi empirycznymi oraz oceną wartości prognostycznej modelu. Jakość modelu można ocenić za pomocą mierników:

1. wariancji składnika resztowego: De² → min;

2. średnich błędu szacunku parametrów strukturalnych: S(a_i) = Se(X^TX)^-1;
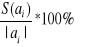
   ; (50% szacowanego parametru);

3. współczynnika zbieżności i determinacji: ϕ² i R² ;
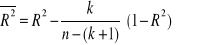
   ; gdzie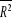
   to skorygowany współczynnik determinacji. ϕ² i R²→1;

4. współczynnika zmienności resztowej: We.

H₀: α_i = 0

H₁: α_i > 0 (!!!) Nie pisać α_i ≠ 0

α_i < 0

Badanie relatywnego wpływu zmiennych objaśniających na zmienną objaśnianą. Do oceny relatywnego znaczenia zmiennej objaśniającej x_i kształtowaniu się zmian zmiennej y wyznacza się współczynnik ważności:

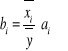
(i=1,2, …, k)

gdzie:

- średnia arytmetyczna zmiennej objaśniającej x_i

- średnia arytmetyczna zmiennej objaśnianej y

a_i - wartość oceny parametru strukturalnego α_i

Im większe b_i, tym relatywnie większy wpływ zmiennej objaśniającej na zmienną objaśnianą modelu.

2003-03-20

BŁĘDY PROGNOZ EX POST I EX ANTE

Wartość prognostyczną modelu określa się przez badanie jakości prognoz ex post i ex ante.

Mierniki prognoz ex post służą do oceny trafności prognoz. Podstawową miarą błędu prognoz ex post jest bezwzględny błąd prognozy (D_T):

D_T = y_t - y_T* T>n

gdzie:

y_t - realizacja zmiennej y w okresie t;

y_T* - prognoza zmiany y na czas T otrzymana z danej metody.

Miernik ten informuje, o jaką wartość różni się rzeczywista wartość zmiennej prognozowanej od postawionej prognozy. Znak „+” oznacza, że rzeczywista wartość jest większa od prognozy. Znak „-„ oznacza, że rzeczywista wartość jest niższa od prognozy.

Względny błąd prognozy ex post (V_T):

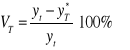
Informuje o ile procent rzeczywista wartość zmiennej prognozowanej odchyla się od postawionej prognozy.

W przypadku, gdy stawiamy ciąg prognoz
dla okresu t = n+1, ..., T to oblicza się średni bezwzględny błąd prognoz (
):

Średni względny błąd prognozy ex post (
):

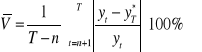
Informuje, jaki procent rzeczywistej wartości zmiennej y stanowiło przeciętnie bezwzględne odchylenie prognoz od danych rzeczywistych.

Wada miernika V_T i śrV - nie spełniają warunków symetrii, tzn. wyżej oceniają przeszacowanie prognoz niż ich niedoszacowanie.

Odchylenie standardowe błędów prognoz ex post (s):

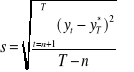
Wartość s informuje, o ile średnio odchylają się zaobserwowane wartości zmiennej prognozowanej od postawionych prognoz.

Relatywną ocenę dokładności prognoz mierzy względny średni błąd prognozy (V):

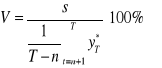
Powyższe wzory nie spełniają warunku unormowania i symetrii. Warunek unormowania, jak i symetrii spełnia dostosowany średni błąd ex post w przedziale weryfikacji (D_s):

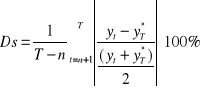
D_s ∈ <0%, 200%>

Gdy w szeregu występują obserwacje nietypowe (szczególnie niskie lub szczególnie wysokie wartości niektórych błędów), a także gdy wartości zmiennej prognozowanej są bliskie 0, należy stosować błędy medianowe.

Procedura:

1. porządkujemy rosnąco błędy (bezwzględne błędy prognozy lub względne błędy prognozy typu ex post);

2. gdy (T - n) jest liczbą nieparzystą, to błąd mediany oznaczony jest numerem
   ;

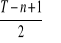
3. gdy (T - n) jest liczbą parzystą, to błąd mediany jest średnią arytmetyczną o numerach:
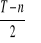
   i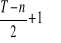
   .

Współczynnik Janusowy:

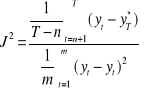
Miernik ten określa relację stopnia dopasowania prognoz i modelu do danych rzeczywistych. Jeżeli J²≤1, to uważa się, że dotychczasowe prognozy są trafne i model może być wykorzystany do prognozowania. Jest to model pożądany.

Współczynnik Theila:

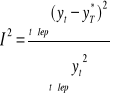
Iep - okres empiryczny weryfikacji prognoz. Jest to przedział, w którym prognoza jest sprawdzana.

I² informuje, jaki jest przeciętny względny błąd prognozy dla rozpatrywanych okresów. Przyjmuje wartość 0, gdy prognozy są idealnie trafne. Im większe są różnice między prognostycznymi i rzeczywistymi wartościami badanej zmiennej, tym większa jest jego wartość.

Na przyczyny nietrafności prognoz wskazują trzy zmiany, które powstają po rozbiciu współczynnika Theila na części składowe:

I² = I₁² + I₂² + I₃²

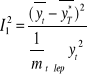
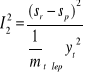
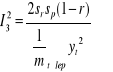
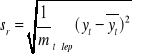
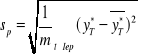
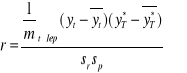
gdzie:

- średnia arytmetyczna rzeczywistych wartości zmiennej prognozowanej w przedziale weryfikacji;

- średnia wartość prognoz w przedziale weryfikacji;

s_r - odchylenie standardowe rzeczywistych wartości y_t w przedziale weryfikacji;

s_p - odchylenie standardowe postawionych prognoz w przedziale weryfikacji;

r - współczynnik korelacji pomiędzy y_t i
;

- wielkość błędów popełnianych z tytułu:

- obciążoności prognozy (nieodgadnięcia średniej wartości zmiennej prognozowanej);

- niedostatecznej elastyczności (nieodgadnięcia wahań zmiennej prognozowanej);

- niedostatecznej zgodności prognoz z rzeczywistym kierunkiem zmian zmiennej prognozowanej (nieodgadnięcia kierunku tendencji rozwojowej).

Powyższe mierniki wyrażone są w postaci względnej.

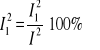
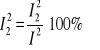
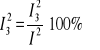
Główną przyczyną powstawania błędów predykcji są błędy wynikające z niezgodności kierunku zmian prognoz ze zmianami realizacji zmiennej prognozowanej.

Rozmiary tych błędów są uzasadnione tym, że stosowane metody prognozowania nie uwzględniają w sposób bezpośredni możliwość zmian dotychczasowego kierunku zmiennej prognozowanej (punktów zwrotnych realizacji zmiennej).

Punkt zwrotny to moment lub okres, w którym następuje załamanie dotychczasowego monotonicznego wzrostu bądź spadku wartości zmiennej prognozowanej w czasie.

Efektywność metod prognozowania zależy od liczby punktów zwrotnych. Maleje w miarę ich wzrostu.

Weryfikacja ex post jest sposobem doskonalenia metodologii prognoz. Systematyczna analiza trafności prognozowania umożliwia ocenę:

1. stopnia niepewności prognozowania poszczególnych zmiennych;

2. osiąganego horyzontu prognozy;

3. źródeł niedoskonałości prognoz;

4. sformułowania rekomendacji, co do dalszego wykorzystania danej metody prognozowania;

5. wyboru tej metody, które dla danej zmiennej daje najmniejsze błędy typu ex post.

Błąd ex ante jest określany przed upływem czasu, na który prognoza została ustalona. Szacowany jest w tym samym czasie, w którym wyznacza się prognozę. Mierniki dokładności prognoz typu ex ante służą do oceny oczekiwanych wielkości odchyleń rzeczywistych wartości zmiennej prognozowanej od postawionych prognoz. Mierniki wykorzystywane są do określenia dopuszczalności prognozy.

Prognoza jest dopuszczalna, gdy obarczona jest przez jej odbiorcę stopniem zaufania wystarczającym do tego, by mogła być wykorzystana w praktyce.

Rząd dokładności wnioskowania w przyszłość jest w praktyce tym lepszy, im niższy jest średni błąd predykcji.

Kryterium dopuszczalności prognozy formułuje się w postaci warunku nałożonego na względny błąd predykcji:

V ≤ σ

gdzie:

σ - liczba dana z góry, zależna od konkretnych warunków i praktycznych potrzeb w zakresie wymaganej dokładności prognoz.

W praktyce prognozy będą dopuszczalne, gdy:

V ≤ 5% - ostre kryterium

lub przy łagodniejszym kryterium:

V ≤ 10%

W przypadku prognoz przedziałowych kryterium dopuszczalności prognoz zapisujemy:

P{|y_t -
| < ε} = γ

ε, γ - dobrane z góry liczby, gdzie ε > 0, 0 < γ < 1

W praktyce ε ustala się na możliwie niskim poziomie, natomiast γ na możliwie wysokim poziomie.

2003-03-27

PROGNOZOWANIE NA PODSTAWIE MODELU TENDENCJI ROZWOJOWEJ

Model tendencji rozwojowej to ekonometryczny model jednorównaniowy, którego jedyną zmienną objaśniającą jest zmienna czasowa t. Modele te są przydatne do prognoz krótko- i średnioterminowych. Tendencja rozwojowa w długim okresie czasu nie jest nigdy stała.

Praktyczne wykorzystanie modeli tendencji rozwojowej posiada wiele zalet:

• do budowy modelu niezbędne są informacje dotyczące jedynie zmiennej prognozowanej;

• nie występuje problem znajomości zmiennych objaśniających w przyszłości;

• (!!!) modele tendencji rozwojowej są w większości przypadków liniowe bądź dające się transformować do postaci liniowej;

• łatwo można ocenić dokładność budowanych prognoz.

Ogólnie model tendencji rozwojowej można zapisać:

1. Y = f(t) + ε t = 1, 2, ..., n - model addytywny

lub

2. Y = f(t)* ε - model multiplikatywny

gdzie:

f(t) - funkcja trendu;

ε - zmienna losowa, która reprezentuje oddziaływanie wahań przypadkowych na tendencję rozwojową o wartości oczekiwanej równej 0 dla 1) i wartości oczekiwanej równej 1 dla 2)

Analityczną postać funkcji można dobrać przez:

1. analizę graficzną (rozrzut punktów empirycznych odpowiadających realizacjom zmiennych y_t w kolejnych okresach czasu);

2. analizę przyrostów zmiennej prognozowanej:

• jeżeli przyrosty są stałe, to mamy do czynienia z liniową funkcją trendu:

• w przypadku funkcji potęgowej względne przyrosty funkcji są odwrotnie proporcjonalne do zmiennej niezależnej;

• w przypadku trendu logistycznego względne przyrosty zmiennej y są malejącą liniową funkcją tej zmiennej.

PREDYKCJA NA PODSTAWIE TRENDU LINOWEGO

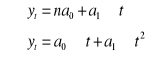
Jeżeli
, to:

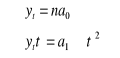
Gdy
, to:

T - macierz zmiennej objaśniającej:

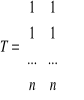
Jakość modelu przeszłości nie jest równoznaczna z jego wartością prognostyczną, a do celu prognozowania wybieramy model dobry w sensie wybranych mierników jakości. Żeby wykorzystać model do budowy prognoz należy założyć:

• stabilność relacji strukturalnych w czasie;

• stabilność rozkładu składnika losowego umożliwiającą ocenę błędu ex ante prognozy.

Przyszłą wartość zmiennej prognozowanej otrzymuje się przez ekstrapolację trendu, tj. podstawianie do modelu w miejsce zmiennej czasowej numeru okresu prognozowania T.

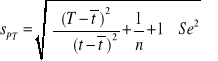
Prognoza przedziałowa:

dla próby małej: n ≤ 120:

dla próby dużej: n > 120:

Dla prognozy przedziałowej obliczamy względny błąd predykcji (V_PT'):

- dla próby małej

- dla próby dużej

EKSTRAPOLACJA NA PODSTAWIE TRENDU

UWZGLĘDNIAJĄCEGO WAHANIA SEZONOWE

Poza tendencją rozwojową na zmienność zjawisk w czasie wpływ mają wahania typu okresowego przyjmujące formę wahań sezonowych. Wahania sezonowe wyznaczane są z szeregów czasowych przez porównanie wartości empirycznych z wartościami teoretycznymi.

W zależności od sposobu tego porównania wyróżniamy wahania:

1. addytywne (bezwzględne, absolutne) - występują, gdy różnice między rzeczywistymi (empirycznymi) wartościami szeregu czasowego a teoretycznymi są względnie stałe:

2. multiplikatywne (względne, relatywne) - występują, gdy iloraz wartości empirycznych i teoretycznych jest względnie stały:

Model przebiegu zjawisk w czasie może mieć postać:

1. addytywną:

t = 1, 2, ..., n

2. multiplikatywną:

t = 1, 2, ..., d

gdzie:

Y_T - poziom empiryczny badanego zjawiska;

- trend zmiennej y

G_it, O_it - wahania okresowe;

- składnik losowy (wahania przypadkowe)

d - liczba cykli podokresowości

Na podstawie próby wyznaczamy aproksymanty funkcji addytywnej (a) i multiplikatywnej (b):

a)

b)

Jeżeli wahania sezonowe mają charakter addytywny, to wyodrębniany jest z modelu przez odejmowanie wartości szeregu empirycznego od wartości szeregu teoretycznego.

gdzie:

n_i - długość empirycznego szeregu czasowego w i-tym cyklu okresowości. W każdym cyklu okresowości długość empirycznego szeregu czasowego jest jednakowa i wynosi dokładnie n_i.

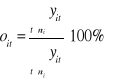
Eksymatory sezonowości g_it i o_it są oczyszczone, jeżeli zachodzą równości:

1)
2)

Dla celów prognozowania wykorzystujemy jedynie mierniki oczyszczone. Gdy nie są spełnione powyższe warunki (1 i 2), to mierniki są surowe i należy je skorygować miernikami korygującymi k:

1)
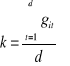
2)

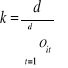
Oczyszczone mierniki sezonowości:

1)
2)

Pomiędzy addytywną i multiplikatywną sezonowością zachodzą powiązania, które można wyznaczyć, gdy model nie ma wyraźnej tendencji rozwojowej.

o_it - to miernik oczyszczony

Wyznaczanie reszt:

1. dla modelu addytywnego:

2. dla modelu multiplikatywnego:

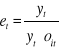
Wariancja składników resztowych:

1. dla modelu addytywnego:

2. dla modelu multiplikatywnego:

Przedstawiona koncepcja wahań sezonowych może być wykorzystana do prognozowania, gdy:

1. w okresie prognozy T nie ulega zmianie tendencja rozwojowa;

2. w okresie prognozy nie ulegają zasadniczej zmianie wahania sezonowe zarówno co do kierunku, jak i siły;

3. w okresie prognozy nie ulęgają zasadniczej zmianie mechanizmy przyczynowe, które określają kształt empirycznego rozkładu reszty.

Prognozy na podstawie trendu z uwzględnieniem wahań sezonowych zapisujemy:

1. dla modelu addytywnego:

2. dla modelu multiplikatywnego:

2003-04-03

PROGNOZOWANIE NA PODSTAWIE JEDNORÓWNANIOWEGO

MODELU EKONOMETRYCZNEGO

Modele jednorównaniowe służą jako narzędzie prognozowania zjawisk o niskim stopniu złożoności. Mogą być wykorzystane do prognoz krótko- i średnioterminowych. Do średniookresowych prognoz wykorzystuje się modele struktury produkcji, konsumpcji, kosztów i wydajności pracy.

Zalety prognozowania opartego o model ekonometryczny to:

• prosta budowa i interpretacja parametrów;

• możliwość obliczeń błędów typu ex ante;

• możliwość uzyskiwania prognoz wariantowych;

• możliwość doboru metod estymacji parametrów w zależności od przyjętych założeń odnośnie składnika losowego (heterostehastyczność składnika losowego bądź autokorelacja - metoda UMNK /uogólniona metoda najmniejszych kwadratów/).

Założenia teorii prognozy ekonometrycznej:

1. znany jest dobry model w sensie kryteriów (Se², S(a_i), ϕ², R², We);

2. występuje stabilność postaci analitycznej modelu oraz stabilność relacji strukturalnych w czasie;

3. składnik losowy ma stały rozkład w czasie;

4. znane są wartości zmiennych objaśniających x_i w okresie prognozowanym. Zmienne te ustala się w oparciu o:

1. funkcje trendów lub modeli ekonometrycznych zbudowanych dla tych zmiennych;

2. wartości ustalone w planach;

3. inne opracowania prognostyczne;

5. można ekstrapolować model poza jego dziedzinę.

Jeżeli w odniesieniu do badanej zmiennej i oddziałujących na nią czynników założenia te są spełnione, to można wykorzystać model ekonometryczny do prognozowania.

Weryfikacja stabilności modelu ekonometrycznego:

1. Badanie stabilności postaci analitycznej modelu - test Ramzey'a. Etapy postępowania:

1. szacujemy parametry modelu ekonometrycznego:

t = 1, 2, ..., n

2. po oszacowaniu modelu obliczamy wartości teoretyczne
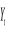
   oraz współczynnik determinacji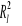
   ;

3. szacujemy parametry następującego modelu:

Sprawdzamy, czy w szacowanym modelu nie pominięto żadnych zmiennych będących drugimi i trzecimi potęgami zmiennych objaśniających;

4. obliczamy współczynnik determinacji z czterema zmiennymi objaśniającymi
   ;

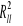
5. badamy istotność przyrostu wartości współczynnika determinacji modelu z punktu c). Obliczamy wartość statystyki F:

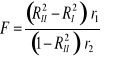
gdzie:

r₁ - liczba nowych zmiennych objaśniających modelu z punktu c);

r₂ - liczba obserwacji minus liczba parametrów modelu;

6. dla wybranego poziomu istotności α weryfikujemy H₀:

H₀: wybór postaci analitycznej modelu jest prawidłowy

H₁: wybór postaci analitycznej modelu jest nieprawidłowy

Statystyka F to test Fishera-Snedecora z liczbą stopni swobody r₁ i r₂. Dla danego poziomu istotności porównujemy F obliczeniowe z F z tablicy Fishera-Snedecora i wówczas:

• jeżeli F > F_α to H₀ odrzucamy na korzyść H₁;

• jeżeli F ≤ F_α to nie ma podstaw do odrzucenia H₀, że wybrana postać analityczna modelu jest prawidłowa.

2. Badanie stabilności parametrów modelu - test Chowa. Etapy postępowania:

1. szacujemy wektor parametrów modelu:

t = 1, 2, 3, ..., n

Dla tego modelu wyznaczamy sumę kwadratów reszt (RSK):

2. dzielimy okres obserwacji t = 1, 2, 3, ..., n na dwa okresy:

• t = 1, 2, ..., n₁

• t = n₁ + 1, n₁ + 2, ..., n

Podział ten może być subiektywny albo może wynikać z analizy zjawiska bądź procesu opisywanego przez model. Można również użyć kryteriów z testu Harrisona-McKeywa:

• gdy n jest parzyste, to:

• gdy n jest nieparzyste, to:

3. szacujemy składowe wektorów równań:

I)
t = 1, 2, n₁

II)
t = n₁ + 1, n₁ + 2, ..., n

4. obliczamy sumy kwadratów reszt modelu I i II (RSK I i RSK II):

5. obliczamy dodatkowo reszty trzecie (RSK III):

RSK III = RSK I + RSK II

oraz wyznaczamy reszty czwarte (RSK IV):

RSK IV = RSK - RSK III

6. wyznaczamy wartości statystyki F:

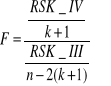
7. obieramy poziom istotności α i weryfikujemy H₀

H₀: parametry modelu są stabilne

H₁: parametry modelu nie są stabilne

Statystyka F ma rozkład Fishera-Snedecora z r₁=k+1 i r₂=n-2(k+1) stopnia swobody. Porównujemy statystykę F obliczeniowe z F z tablic Fishera-Snedecora i wówczas:

• jeżeli F > F_α to H₀ odrzucamy na korzyść H₁, czyli parametry modelu nie są stabilne;

• jeżeli F ≤ F_α to nie ma podstaw do odrzucenia H₀, że parametry są stabilne.

Powyższe założenia uzupełniane są dwoma postulatami teorii predykcji:

1. dla każdej prognozy ekonometrycznej powinna być obliczona wartość miernika określającego stopień dokładności predykcji;

2. prognozę należy budować w ten sposób, żeby miernik określający stopień dokładności predykcji był jak najmniejszy.

Na podstawie jednorównaniowego modelu ekonometrycznego buduje się prognozy punktowe i przedziałowe.

Prognoza punktowa:

gdzie:

- zmienne objaśniające z przyszłości

Efektywność prognozy obliczana jest za pomocą średniego błędu prognozy ex ante:

gdzie:

- transponowany wektor zmiennych objaśniających z przyszłości

Średni błąd prognozy:

Prognoza przedziałowa:

1. dla n > 30

2. dla n ≤ 30

Błędy prognoz:

1. dla n > 30

2. dla n ≤ 30

Średni błąd szacunku:

1. dla n > 30

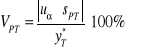
2. dla n ≤ 30

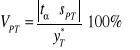
W sytuacji, gdy dysponujemy kilkoma modelami ekonometrycznymi opisującymi tą samą zmienną objaśnianą i jakościowo dobrymi - w wyborze jednego z nich przydatne są mierniki:

• skorygowany współczynnik determinacji;

• kryterium Schwarza (SC):

• kryterium błędu predykcji (FPE):

Wybór modelu następuje na podstawie minimalnej wielkości S.C. lub FPE

SYMULACJA NA PODSTAWIE MODELU EKONOMETRYCZNEGO

Symulacja to każdy proces, którego celem jest zbadanie zachowania pewnego sztucznego układu lub poznanie określonych jego charakterystyk. Poznany obiekt, zjawisko bądź zdarzenie nazywamy systemem przedmiotowym, zaś układ sztuczny nazywamy modelem.

Podstawową rolę w metodzie symulacyjnej odgrywa model badanego systemu realnego. Posługiwanie się modelem, a nie systemem wynika z przyczyn:

• system taki może jeszcze nie istnieć;

• system realny może istnieć, ale może być tak skomplikowany, że bezpośrednie jego badanie jest niemożliwe;

• badanie może mieć na celu zweryfikowanie słuszności budowanej teorii o cechach charakterystycznych badanego systemu realnego lub o jego funkcjach bądź zachowaniach.

Model musi wiernie odwzorowywać naśladowany przez siebie system przedmiotowy. Jakość wyników badania prowadzonego metodą symulacji zależy od dokładności, z jaką przyjęty model odzwierciedla system przedmiotowy.

Symulacja na podstawie modelu ekonometrycznego ma dać odpowiedź na pytania:

• jakie byłyby wartości zmiennych objaśnianych, gdyby zmienne objaśniające przyjęły określoną wartość;

• jak należałoby dobrać wartości zmiennych objaśniających, żeby uzyskać określone wartości zmiennych objaśnianych.

Zatem symulacja na podstawie modelu ekonometrycznego może dotyczyć:

• zmiennych;

• parametrów strukturalnych;

• właściwości składnika losowego.

Rodzaje symulacji:

1. deterministyczna - występuje, gdy oszacowane parametry modelu nie zmieniają się w czasie eksperymentu;

2. stochastyczna - gdy zakłócenia wprowadzone do modelu przyjmują wartości losowe.

Inny podział:

1. prosta - mamy z nią do czynienia, gdy zmienione są wartości tylko jednej zmiennej objaśniającej;

2. złożona - gdy jednocześnie zmieniane są wartości kilku zmiennych objaśniających.

W wyniku symulacji uzyskujemy różne warianty obiektu opisywanego przez model. Jeżeli symulacja dotyczy przyszłego zachowania obiektu, to te uzyskane warianty, których prawdopodobieństwo jest wystarczające dla celów praktycznych, mogą być traktowane jako prognoza.

2003-04-24

WYBRANE METODY PROGNOZOWANIA NA PODSTAWIE

SZEREGÓW CZASOWYCH

W szczególnym przypadku, gdy w szeregu występuje stały poziom zjawiska i wahania przypadkowe do prognozowania wykorzystuje się:

1. metody naiwne - oparte są na założeniu, że w przyszłości nie nastąpią zmiany w sposobie oddziaływania czynników, które mają wpływ na zmienną prognozowaną. Można je stosować, gdy w szeregu statystycznym występuje składowa systematyczna w postaci stałego przeciętnego poziomu oraz niewielkie wahania przypadkowe. Do oceny siły wahań przypadkowych należy zastosować współczynnik zmienności:

V powinno być stosunkowo niskie. Najbardziej popularną metodą jest ta, według której prognoza:

gdzie:

- prognoza zmiennej Y wyznaczona na moment T;

- wartość zmiennej prognozowanej w okresie (t - 1).

Do oceny trafności prognozy można wykorzystać względny błąd prognoz ex post:

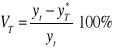
Jeżeli błąd ten nie przekroczy zakładanego procentu, np. 5% to prognozę uznaje się za trafną;

2. metody średniej ruchomej - służą do wygładzania szeregu statystycznego, a także są wykorzystywane do prognozowania. Wśród tych modeli wyróżniamy:

1. model średniej ruchomej prostej - w modelu tym przyjmuje się za prognozę średnią arytmetyczną z k-ostatnich wartości zmiennych:

gdzie:

- prognoza zmiennej Y w okresie lub momencie T

k - stała wygładzania

- wartość zmiennej prognozowanej w okresie i

Stałą k wybiera się na podstawie najmniejszego błędu ex post, np. średni względny błąd prognozy ex post. Liczbę k może również określić prognosta. Prognoza wyznaczona z mniejszej liczby wyrazów szybciej odzwierciedla zmiany zachodzące w wartościach zmiennej prognozowanej, ale większy wpływ będą wywierały wahania przypadkowe. Sugeruje się, by przy prognozowaniu krótkookresowym (miesiąc lub nieco więcej) dla danych miesięcznych k wynosiło 3 lub 5:

k = 3 lub k = 5

2. model średniej ruchomej ważonej - w modelu tym wykorzystywana jest zasada postarzania informacji (dane nowsze zawierają bardziej aktualne informacje o prognozowanym zjawisku, zatem posiadają większe wagi niż dane starsze)

gdzie:

- waga nadana przez prognostę wartości zmiennej prognozowanej w momencie lub okresie i

Warunki stosowania modelu średniej ruchomej:

• poziom zmiennej prognozowanej w rozpatrywanym okresie jest prawie stały z niewielkimi odchyleniami losowymi;

• w szeregu czasowym nie występują tendencje rozwojowe, ani też wahania sezonowe.

3. modele wygładzania wykładniczego - istota tych modeli polega na tym, że szereg wygładza się za pomocą ważonej średniej ruchomej. Wagi określa się według reguły wykładniczej. Najbardziej znane modele to:

1. prosty model wygładzania wykładniczego - ma zastosowanie, gdy w szeregu czasowym występuje prawie stały poziom zmiennej prognozowanej i wahania przypadkowe. Prognoza zmiennej na okres T:

gdzie:

α - parametr wygładzania, który dobiera się eksperymentalnie konstruując prognozy dla różnych
i wybierając tę wartość, dla której błąd dla prognoz wygasłych jest najmniejszy.

Dla
wagi α, α(1 - α) i α(1 - α)² mają wartości wykładniczo malejące.

Jeżeli α dąży do 1, to prognoza będzie uwzględniała w wysokim stopniu błędy ex post poprzednich prognoz. Natomiast wartość α bliskie 0 oznaczają, że prognoza tylko w niewielkim stopniu będzie uwzględniała błędy poprzednich prognow.

Za wartość początkową
przyjmuje się:

• pierwszą wartość rzeczywistą zmiennej prognozowanej y₁;

• średnią arytmetyczną rzeczywistych wartości zmiennej prognozowanej;

• tę wielkość α, dla której błąd prognoz wygasłych jest najmniejszy

1. model liniowy Holta - jeżeli w szeregu czasowym występuje tendencja rozwojowa i wahania przypadkowe, do wygładzania szeregu stosuje się model liniowy Holta. Jest to model dwurównaniowy. Równanie pierwsze służy do wyznaczenia wygładzonych wartości szeregu czasowego w momencie lub okresie (t - 1):




Równanie drugie służy do wyznaczenia wygładzonych wartości przyrostu trendu na moment bądź okres (t - 1):




gdzie:


- parametry wygładzania o wartości z przedziału <0,1>

F_t-1 - wygładzona wartość zmiennej prognozowanej na moment lub okres (t-1)

S_t-1 - wygładzona wartość przyrostu trendu na moment lub okres (t-1)

Wartości α i β dobiera się na podstawie najmniejszego błędu ex post, np. względnego bądź kwadratowego.

Prognoza Holta:


T>n

Skąd wziąć wartości początkowe F₁ i S₁?

Lp.	F1	S1
1	y1	0
2	y1	y2 - y1
3	za F1 przyjmujemy wyraz wolny liniowej funkcji trendu oszacowany na podstawie próbki wstępnej, np. kilka pierwszych obserwacji	współczynnik kierunkowy liniowej funkcji trendu oszacowany na podstawie próbki wstępnej

2. model Wintersa - jest stosowany, gdy szereg czasowy zawiera tendencją rozwojową, wahania przypadkowe i sezonowe. Prognozę otrzymuje się wykorzystując trzy równania zawierające trzy parametry wygładzania (dochodzi γ). Model Wintersa występuje w postaci addytywnej i multiplikatywnej:

• postać addytywna:










• postać multiplikatywna:










gdzie:

F_t-1 - wygładzona wartość zmiennej prognozowanej w momencie lub okresie (t-1) po wyeliminowaniu wahań sezonowych

S_t-1 - ocena przyrostu trendu w okresie (t-1) bądź momencie

C_t-1 - ocena wskaźnika sezonowości na okres (t-1) bądź moment

r - długość cyklu sezonowości;


- parametry z przedziału <0,1>

Prognoza na okres T>n:

• dla modelu addytywnego:




• dla modelu multiplikatywnego:




Parametry
dobiera się:

• przez minimalizację średniego kwadratowego błedu prognoz wygasłych;

• 
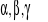
  bliskie 1, gdy składowe szeregu zmieniają się szybko;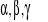

• 
  bliskie 0, gdy składowe szeregu zmieniają się powoli.

Za wielkości początkowe F₁, S₁ i C₁ przyjmuje się:

• F₁ - pierwszą wartość zmiennej prognozowanej, tj. y₁ lub średnią z wartości zmiennej w pierwszym cyklu;

• S₁ - różnicę pierwszej i drugiej zmiennej prognozowanej, tj. (y₂ - y₁) lub różnice średnich wartości wyznaczonych dla pierwszego i drugiego cyklu;

• C₁ - dla modelu addytywnego: średnią różnic odpowiednią tej samej fazie cyklu sezonowości wartości zmiennej prognozowanej i wygładzonych wartości trendu; dla modelu multiplikatywnego: ilorazy wartości zmiennej z pierwszego cyklu w odniesieniu do średniej wartości w pierwszym cyklu.

2003-05-15

METODA WAG HARMONICZNYCH

Metoda oparta na wagach harmonicznych dotyczy zasady postarzania informacji. Twórcą metody jest prof. Helwig. W metodzie tej wyróżniamy dwa niezależne etapy:

Etap 1. Wyrównywanie szeregu za pomocą trendu pełzającego.

Etap 2. Ekstrapolacja trendu metodą wag harmonicznych.

Trend pełzający (ruchomy) stosowany jest do opisu kształtowania zjawiska w czasie, gdy charakteryzuje się ono nieregularnymi zmianami. Nie zakłada się z góry postaci analitycznej zjawiska. Procedura wyznaczania trendu pełzającego polega na wygładzeniu szeregu czasowego o długość n wyrazów. Przyjmuje się, że szereg czasowy powinien być wystarczająco długi (mieć więcej niż 10 jednostek). Wygładzanie szeregu przebiega etapami:

1. zakłada się, że znany jest szereg czasowy (y₁, y₂, ..., y_n) niemonotonicznie rosnący. Ustalamy tu stałą k, która jest stałą wygładzania, ale tak, by k<n; k jest liczbą naturalną należącą do zbioru (2, 3, ..., n);

2. szacuje się za pomocą metody KMNK parametry równania odcinków liniowych:


(t = 1, 2, ..., k)


(t = 2, 3, ..., k+1)

........................................................


(t = n-k+1, ..., n)

3. na podstawie oszacowanych trendów liczbowych wyznaczamy wartości teoretyczne (
   );

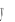
4. ostateczne wygładzanie szeregu następuje w wyniku obliczenia średniej z wartości teoretycznych dla każdego momentu (
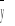
   ). Łącząc kolejne punkty o współrzędnych (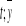
   ) odcinkami prostymi otrzymuje się wykres trendu badanego szeregu czasowego w postaci łamanej zwanej trendem pełzającym. Oszacowany model trendu pełzającego jest podstawą przewidywania przyszłych wartości zmiennej prognozowanej. W tym celu dokonuje się ekstrapolacji trendu w przyszłość według metody wag harmonicznych.

Procedura metody wag harmonicznych:

1. oblicza się przyrosty funkcji trendu:


(
)

2. wyznacza się współczynniki
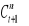
   , które nazywane są wagami harmonicznymi. Mają one na celu uwzględnienie zasady postarzania informacji.


(t = 1, 2, ..., n-1)

Przyrosty wag przypisywane są kolejnym wyrazom szeregu czasowego. Są odwrotnie proporcjonalne do wieku danych. Informacjom starszym nadaje się mniejsze wagi, nowszym - większe. Wagi harmoniczne są zawsze nieujemne. Ich suma jest równa 1:


(
)

3. określa się średnią przyrostu (
   ):




4. wyznacza się odchylenia standardowe przyrostów trendu pełzającego (s):




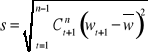
Prognoza punktowa:


(T>n)

Prognoza przedziałowa:







d(T) - dolna granica prognozy

g(T) - górna granica prognozy




k - zmienna u_α lub t_α

Główną zaletą tej metody jest brak wyraźnej tendencji rozwojowej.

Przykład:

Sprzedaż multimedialnych programów do nauki języka angielskiego w sztukach w pewnej księgarni od kwietnia do grudnia 2002 roku kształtowała się następująco:

65, 63, 64, 65, 63, 64, 65, 62, 63.

Wyznacz prognozę punktową metodą wag harmonicznych na marzec 2003 roku.

n = 9

1° Zakładamy, że k = 3

2° Zakładamy, że szereg wygładzamy metodą trendu pełzającego i tendencji rozwojowych będzie:

n - k + 1 = 9 - 3 + 1 =7

dla t = 1, 2, 3 [65, 63, 64] - I tendencja rozwojowa

dla t = 2, 3, 4 [63, 64, 65] - II tendencja rozwojowa

dla t = 3, 4, 5 [64, 65, 63] - III tendencja rozwojowa

dla t = 4, 5, 6 [65, 63, 64] - IV tendencja rozwojowa

dla t = 5, 6, 7 [63, 64, 65] - V tendencja rozwojowa

dla t = 6, 7, 8 [64, 65, 62] - VI tendencja rozwojowa

dla t = 7, 8, 9 [65, 62, 63] - VII tendencja rozwojowa

Wyznaczamy 7 tendencji rozwojowych:


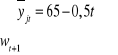
(t = 1, 2, 3)


(t = 2, 3, 4)


(t = 3, 4, 5)


(t = 4, 5, 6)


(t = 5, 6, 7)


(t = 6, 7, 8)


(t = 7, 8, 9)

Na podstawie oszacowanych trendów liniowych obliczamy wielkości teoretyczne wygładzone wartością trendów s segmentowych wyznaczonych z równań oraz średnie wielkości wszystkich wygładzeń.

t
1 2 3 4 5 6 7 8 9	64,5 64,0 63,5	63,0 64,0 65,0	64,5 64,0 63,5	64,5 64,0 63,5	63,0 64,0 65,0	64,67 63,67 62,67	64,33 63,33 62,33	64,50 127,00 192,00 193,50 190,50 192,17 193,00 126,00 62,33	64,5 63,5 64,0 64,5 63,5 64,1 64,3 63,0 62,33	- -1,0 0,5 0,5 -1,0 0,6 0,2 -1,3 -0,67	- 0,016 0,034 0,054 0,079 0,111 0,152 0,215 0,339	- -0,0160 0,0170 0,0270 -0,0790 0,0666 0,0304 -0,2795 -0,2373	- 0,2910 0,9228 0,9228 0,2910 1,1249 0,4364 0,7046 0,0438	- 0,004656 0,031375 0,049831 0,022989 0,124864 0,066333 0,151489 0,014848
											1,000	-0,4606		0,466385







PROGNOZOWANIE NA PODSTAWIE MODELI HEURYSTYCZNYCH

Prognozowanie heurystyczne jest to przewidywanie na podstawie opinii ekspertów oparte na doświadczeniu i intuicji. Prognozowanie przyszłości polega na ukazywaniu możliwych wariantów rozwoju i wskazywaniu najbardziej realistycznych. Proponowane prognozy mogą być jakościowe i ilościowe.

Prognozowanie heurystyczne jest wykorzystywane do:

• badania poziomu badanego zjawiska;

• wskazywania dat zajścia interesującego nas zdarzenia;

• określania punktów zwrotnych przebiegu zmiennych;

• określania prawdopodobieństwa występowania danego zdarzenia;

• określania natężenia występowania nowych zjawisk;

• oceny przydatności tworzonych modeli do prognozowania.

Największe zastosowanie wśród metod heurystycznych mają:

1. burza mózgów

2. metoda delficka

16

---