Oblicz pięć początkowych wyrazów ciągu
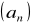
określonego wzorem:
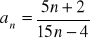
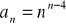
.Podaj definicję ciągu liczbowego. Ciąg
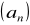
dany wzorem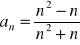
. Oblicz pierwszy i dziesiąty wyraz ciągu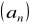
. Wyznacz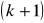
wyraz ciągu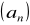
.Oblicz wyraz:
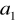
,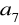
,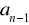
,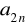
ciągu o wyrazie ogólnym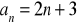
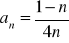
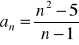
Dany jest ciąg
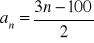
.Oblicz piętnasty wyraz tego ciągu.
Którym wyrazem tego ciągu jest liczba 10?
Ile wyrazów ujemnych ma ten ciąg?
Dany jest ciąg
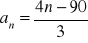
.Oblicz dwudziesty wyraz tego ciągu.
Którym wyrazem tego ciągu jest liczba 50?
Ile wyrazów ujemnych ma ten ciąg?
Które wyrazy każdego z ciągów
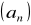
i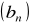
są równe liczbom: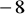
; 0; 8, jeżeli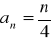
;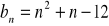
?Podaj definicję ciągu rosnącego. Wykaż, że ciąg
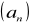
jest ciągiem rosnącym.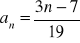
.Wykaż, że ciąg
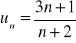
jest rosnący.Zbadaj monotoniczność ciągu:
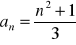
. Sporządź wykres tego ciągu.Zbadaj monotoniczność ciągu:
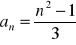
. Sporządź wykres tego ciągu.Zbadaj monotoniczność ciągu:
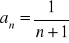
. Sporządź wykres tego ciągu.Zbadaj monotoniczność ciągu:
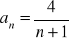
. Sporządź wykres tego ciągu.Zbadaj monotoniczność ciągów określonych wzorami:
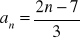
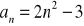
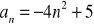
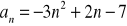
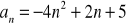
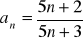
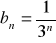
Zbadaj monotoniczność ciągu:
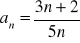
.Zbadaj monotoniczność ciągu:
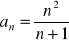
.Zbadaj, który z poniższych ciągów jest arytmetyczny, który geometryczny:
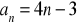
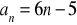
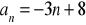
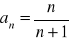
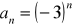
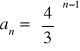
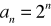
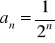
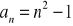
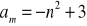
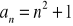
Podaj definicję ciągu arytmetycznego. Czy ciąg
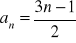
jest arytmetyczny?Napisz 5 początkowych wyrazów ciągu arytmetycznego
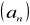
, jeżeli: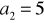
,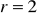
.Napisz trzy początkowe wyrazy ciągu arytmetycznego
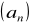
, jeśli wiadomo, że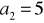
,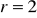
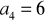
,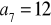
Wyznacz ciąg arytmetyczny
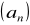
mając dane: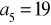
i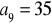
.W ciągu arytmetycznym
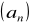
z czterech liczb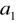
,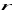
,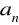
,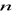
, dane są trzy. Wyznacz brakującą.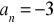
,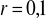
,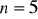
,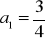
a,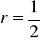
,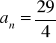
Liczby 3 i 7 są dwoma początkowymi wyrazami pewnego rosnącego ciągu arytmetycznego. Oblicz dwudziesty wyraz tego ciągu i sumę jego dwudziestu początkowych wyrazów.
Liczby 5 i 8 są dwoma początkowymi wyrazami pewnego rosnącego ciągu arytmetycznego. Oblicz trzydziesty wyraz tego ciągu i sumę jego trzydziestu początkowych wyrazów.
W ciągu arytmetycznym
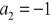
,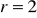
, oblicz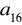
i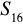
.Wyznacz ciąg arytmetyczny, jeżeli:
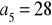
,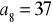
.Ciąg arytmetyczny
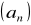
spełnia warunki: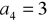
i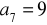
. Oblicz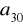
oraz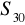
.Wiedząc, że ciąg
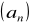
jest ciągiem arytmetycznym oraz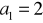
i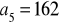
, oblicz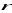
i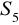
.W ciągu arytmetycznym dane są:
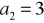
,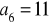
. Oblicz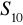
.Oblicz sumę:
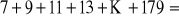
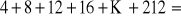
.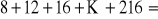
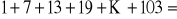
Rozwiąż równanie:
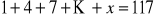
.Oblicz sumę wszystkich liczb dwucyfrowych.
Oblicz sumę wszystkich liczb dwucyfrowych podzielnych przez 3.
Oblicz sumę wszystkich liczb naturalnych dwucyfrowych, które przy dzieleniu przez 5 dają resztę 2.
Oblicz sumę wszystkich liczb naturalnych dwucyfrowych, które przy dzieleniu przez 4 dają resztę 3.
Oblicz sumę wszystkich liczb dwucyfrowych, których reszta z dzielenia przez 3 jest równa 2.
Pan Malinowski pożyczył od swojego kuzyna pewną sumę pieniędzy na remont samochodu. Zobowiązał się do zwrotu pożyczki w dwunastu równych ratach, z których każda była o 30 zł większa od poprzedniej. Ostatnia rata wynosiła 400 zł. Oblicz kwotę pożyczoną przez pana Malinowskiego.
Wartość użytkowa pewnej maszyny malała z roku na rok w postępie arytmetycznym. Po ilu latach maszyna całkowicie straciła wartość użytkową, jeżeli wiadomo, że jej wartość po 18 latach była dwa razy mniejsza niż jej wartość po 4 latach.
Długości boków trójkąta tworzą ciąg arytmetyczny o różnicy 2, a ich iloczyn jest równy 480. Oblicz promień okręgu wpisanego w ten trójkąt.
(*) Wykaż, że jeżeli liczby
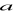
,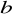
,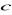
są kolejnymi wyrazami pewnego ciąg arytmetycznego, to liczby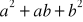
,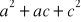
,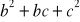
także tworzą ciąg arytmetyczny.Ciągi
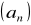
,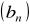
,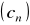
i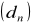
są określone wzorami ogólnymi: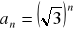
;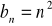
;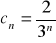
;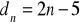
. Zbadaj, który z ciągów jest geometryczny.Podaj definicję ciągu geometrycznego. Czy ciąg
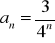
jest geometryczny?Wyznacz ciąg geometryczny, jeżeli:
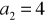
,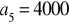
.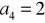
,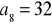
.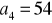
,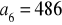
.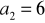
,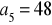
.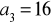
,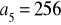
.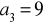
i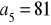
.Dany jest ciąg geometryczny
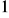
,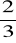
,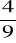
, …. Oblicz sumę siedmiu początkowych wyrazów tego ciągu.Wiedząc, że ciąg jest geometryczny i mając dane
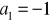
,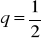
,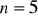
, znajdź: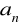
i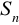
.O ciągu geometrycznym
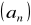
wiemy, że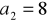
i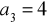
. Oblicz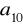
i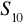
.Oblicz sumę:
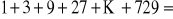
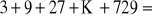
Liczby 2 i 4 są dwoma początkowymi pewnego malejącego ciągu geometrycznego. Oblicz dziesiąty wyraz ciągu i sumę jego dziesięciu początkowych wyrazów.
Oblicz pierwszy wyraz i iloraz ciągu geometrycznego
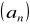
, wiedząc, że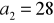
i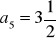
. Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.Oblicz pierwszy wyraz i iloraz ciągu geometrycznego
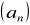
, wiedząc, że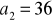
i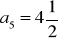
. Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.Wyznacz
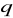
i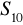
ciągu geometrycznego wiedząc, że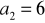
,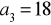
.Wiedząc, że ciąg
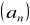
jest ciągiem geometrycznym oraz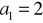
i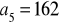
, oblicz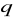
i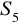
.Liczba mieszkańców w pewnym mieście w ciągu ostatnich lat zwiększała się średnio o
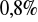
rocznie i obecnie wynosi około 150000. Zakładając, że tempo wzrostu się nie zmieni, oszacuj, ilu ludzi będzie mieszkać w tym mieście za 10 lat.Liczba mieszkańców w pewnym mieście w ciągu ostatnich lat zwiększała się średnio o
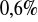
rocznie i obecnie wynosi około 200000. Zakładając, że tempo wzrostu się nie zmieni, oszacuj, ilu ludzi będzie mieszkać w tym mieście za 10 lat.Wpłacono do banku 10000 zł na lokatę oprocentowaną na 12 % w stosunku rocznym. Oblicz stan lokaty po dwóch latach, bez uwzględniania podatku od odsetek, jeżeli dopisywanie odsetek jest:
roczne;
miesięczne.
Uwaga! Jeśli nie dysponujesz kalkulatorem, wystarczy, że jako rozwiązanie podasz odpowiednie wyrażenie zawierające dane z zadania. Jeśli chcesz policzyć wszystko do końca, wynik możesz WYJĄTKOWO podać w przybliżeniu.
Pan Bogdan wpłacił 4000 zł na lokatę półroczną, której oprocentowanie wynosi 6% w skali roku. Ile będzie wynosił stan konta po pięciu latach oszczędzania.
Pan Antoni wpłacił 5000 zł na lokatę 3-miesięczną, której oprocentowanie wynosi 4% w skali roku. Ile będzie wynosił stan konta po trzech latach oszczędzania?
Przedsiębiorca otrzymał z banku 100000 zł kredytu. Oprocentowanie kredytu wynosi p % rocznie, przy czym odsetki dolicza się po upływie każdego roku (kapitalizacja roczna). Po dwóch latach niespłacenia kredytu zobowiązania przedsiębiorcy wobec banku z tego tytułu wynosiły 150000 zł. Ile wynosił procent p? Uwaga! Wynik możesz WYJĄTKOWO podać w przybliżeniu.
Kowalski co miesiąc wpłaca 200 zł na fundusz emerytalny, w którym oprocentowanie wynosi p % i odsetki dopisywane są co miesiąc. Jaki kapitał zgromadzi Kowalski w funduszu emerytalnym po 30 latach?
Pan Malinowski wpłacił do banku na roczną lokatę kwotę w wysokości 30000 zł. Roczne oprocentowanie wynosi 5%. Oblicz odsetki od tej kwoty, jeżeli pieniądze były utrzymywane przez 4 lata oraz:
odsetki były kapitalizowane;
odsetki nie były kapitalizowane.
Pan Malinowski wpłacił do banku na roczną lokatę kwotę w wysokości 20000 zł. Roczne oprocentowanie wynosi 4,5%. Oblicz odsetki od tej kwoty, jeżeli pieniądze były utrzymywane przez 4 lata oraz:
odsetki były kapitalizowane;
odsetki nie były kapitalizowane.
Pan Kowalski zaciągnął kredyt w wysokości 80000 zł na okres 6 lat przy oprocentowaniu rocznym 9%. Oblicz odsetki od tej kwoty, jeżeli:
odsetki były kapitalizowane;
odsetki nie były kapitalizowane.
Pan Kowalski zaciągnął kredyt w wysokości 30000 zł na okres 6 lat przy oprocentowaniu rocznym 18%. Oblicz odsetki od tej kwoty, jeżeli:
odsetki były kapitalizowane;
odsetki nie były kapitalizowane.
(*) Wykaż, że jeżeli liczby
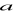
,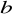
,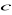
są kolejnymi wyrazami pewnego ciąg geometrycznego, to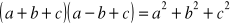
.(*) Ciąg
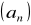
określony jest wzorem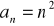
, zaś ciąg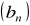
wzorem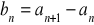
. Wykaż, że ciąg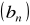
jest arytmetyczny.Liczby 3,
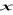
,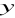
tworzą ciąg arytmetyczny, natomiast liczby 3,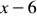
,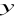
- ciąg geometryczny. Wyznacz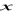
i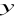
.Liczby
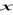
, 7,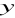
tworzą ciąg arytmetyczny natomiast liczby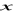
,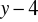
, 32 ciąg geometryczny. Wyznacz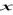
,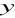
.Liczby
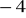
,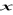
,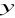
tworzą ciąg arytmetyczny natomiast liczby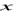
,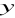
, 36 ciąg geometryczny. Wyznacz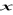
,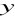
.Podaj definicję ciągu liczbowego. Wyznacz liczby
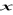
,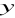
tak, aby liczby -4,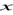
,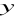
tworzyły ciąg arytmetyczny a liczby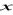
,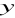
, 50 ciąg geometryczny.Dane są liczby 1,
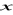
, 9,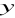
. Znajdź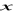
,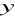
jeżeli pierwsze trzy liczby tworzą ciąg geometryczny, a trzy ostatnie - ciąg arytmetyczny.Trzy liczby, których suma równa się 62 tworzą ciąg geometryczny. Jeżeli do pierwszej dodamy 3, a od trzeciej odjąć 35 to otrzymamy ciąg arytmetyczny. Znajdź te liczby.
Suma trzech liczby będących kolejnymi wyrazami ciągu geometrycznego jest równa 13. Jeżeli do pierwszej dodamy 2, do drugiej 8, a do trzeciej 4 to otrzymamy trzy kolejne wyrazy ciągu arytmetycznego. Znajdź te liczby.
Trzy liczby, których suma równa się 28 tworzą ciąg geometryczny. Jeżeli do drugiej dodamy 1, a od trzeciej odejmiemy 2 to otrzymamy ciąg arytmetyczny. Znajdź te liczby.
Trzy liczby tworzą ciąg geometryczny. Suma kwadratów tych liczb wynosi 364. Jeżeli do pierwszej dodamy 5, do drugiej 7, do trzeciej 1, to otrzymamy ciąg arytmetyczny. Znajdź te liczby.
Trzy liczby są kolejnymi początkowymi rosnącego ciągu arytmetycznego. Gdy do pierwszej z nich dodamy 8, a drugą i trzecią pozostawimy bez zmian, to otrzymamy kolejne początkowe wyrazy ciągu geometrycznego, których suma jest równa 26. Wyznacz te ciągi.
W prostokąt o bokach
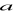
i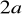
wpisujemy czworokąt tak, że jego wierzchołki są środkami boków prostokąta, a następnie w analogiczny sposób wpisujemy kolejny czworokąt itd. Oblicz sumę pól wszystkich utworzonych w ten sposób czworokątów.Oblicz sumę wszystkich wyrazów nieskończonego ciągu geometrycznego, w którym
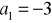
,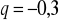
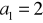
,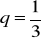
Oblicz sumę nieskończonego ciągu geometrycznego
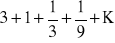
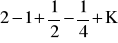
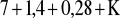
Ułamek dziesiętny okresowy zamień na ułamek zwykły.
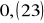
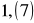
Dana jest funkcja
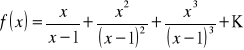
, gdzie prawa strona jest sumą wyrazów nieskończonego ciągu geometrycznego zbieżnego. Znajdź dziedzinę tej funkcji.Rozwiąż:
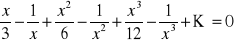
Rozwiąż:
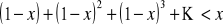
.Znajdź wartość parametru
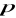
, dla której granica ciągu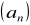
określonego wzorem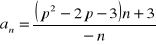
jest równa 4. Zbadaj monotoniczność ciągu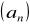
dla znalezionej wartości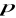
.Dany jest ciąg o wyrazie ogólnym
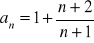
.Zbadaj monotoniczność ciągu.
Oblicz granicę tego ciągu.
Oblicz granicę ciągu
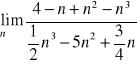
.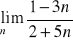
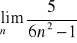
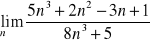
Wyszukiwarka