1. Tor elementu płynu (definicja + równanie). Czy tory elementu płynu mogą się przecinać?
Torem elementu płynu nazywamy linię, którą zakreślił w czasie ruchu element płynu traktowany jako punkt materialny.
![]()
W przepływie ustalonym przez dowolny punkt Mo przechodzi tylko jeden tor elementów płynu.
W przepływie nieustalonym tory elementów punktu mogą się przecinać (nie odbywa się to w jednym czasie, myślowe linie zakreślone przed różne elementy toru mogę się przecinać).
2. Linia prądu (definicja + równanie). Czy linie prądu mogą się przecinać?
Linią prądu nazywamy linię wektorowego pola prędkości, do której wektory prędkości są styczne w danej chwili.
![]()
Linie prądu nie mogą się przecinać, ponieważ w przeciwnym wypadku w punkcie przecięcia prędkości byłaby nieokreślona (równocześnie dwie wartości, co jest niemożliwe).
3. Pochodna substancjalna f(x(t),y(t),z(t)) pochodna [zwyczajna d/dt]
Pochodna substancjalna d/dt jest równa sumie pochodnej lokalnej ![]()
oraz pochodnej konwekcyjnej ![]()
. Dzięki zastosowaniu operatora Hamiltona ![]()
można przedstawić pochodna zwyczajną dowolnej funkcji opisującej ruch płynu.
Przykład dla wielkości A=A[t,x(t),y(t),z(t)]:
![]()
i ![]()
![]()
4. Wzór manometryczny (manometr „pionowy” i „manometr pochyły”) ![]()
- wzór manometryczny, w przypadku gdy różnicę ciśnień mierzymy w ośrodku gazowym, np. w powietrzu, ciężar właściwy ośrodka jest pomijalnie mały w porównaniu z ciężarem właściwym cieczy manometrycznej
![]()
- sumaryczna wysokość słupa
![]()
- wysokość dla manometru jednorurowego pionowego
![]()
wysokość dla manometru pochyłego
![]()
- wysokość dla manometru U-kształtnego pionowego
F - przekrój zbiornika
f - przekrój rurki
γ - ciężar właściwy cieczy
l - przesunięcie menisku cieczy wzdłuż osi rurki
Dokładność pomiaru rośnie wraz ze zmniejszaniem kąta α.
![]()
i ![]()
5. Jaką zasadę zachowania wyraża równanie ciągłości?
Wyraża zasadę zachowania masy. W zamkniętym układzie fizycznym masa płynu nie może powstać ani ulec zniknięciu.
6. Równanie Bernoulliego dla płynu idealnego. Jaką zasadę zachowania wyraża to
równanie?
Całkę Bernoulliego rozpatrujemy dla przepływu ustalonego (wtedy tory ruchu pokrywają się z liniami prądu), jeśli płyn jest barotropowy (gęstość jest tylko funkcją ciśnienia / lub stała) i siła masowa ma potencjał U. Całkowanie wykoujemy wzdłuż linii prądu.
Równanie Bernoulliego wyraża zasadę zachowanie energii wzdłuż linii prądu.
![]()
;
W polu grawitacji ziemskiej w układzie współrzędnych z osią z skierowaną pionowo ku górze potencjał siły masowej jest równy U=-gz.
![]()
. W przypadku płynu nieściśliwego ρ=idem równanie przyjmuje postać: ![]()
![]()
- jednostkowa energia kinetyczna;
![]()
- jednostkowa energia potencjalna wysokości położenia;
![]()
- jednostkowa energia potencjalna ciśnienia
C - stała wzdłuż linii prądu
Suma energii kinetycznej, potencjalnej wysokości oraz potencjalnej ciśnienia każdego elementu płynu leżącego na tej samej linii prądu jest wielkością stałą w przepływie ustalonym.
7. Równanie Bernoulliego dla cieczy rzeczywistej.
![]()
Lub
![]()
- równość sum naporów
Gdzie ![]()
to straty naporu całkowitego.
Równanie Bernoulliego dla cieczy rzeczywistej jest bilansem energii z uwzględnieniem strat. Energia tracona przez ciecz na rozpatrywanym odcinku strumienia zmienia się nieodwracalnie na energię cieplną, przez co następuje zmniejszenie naporu całkowitego.
8. Wymień rodzaje podobieństwa przepływów i krótko je scharakteryzuj.
Dwa przepływy będziemy nazywać podobnymi, jeśli będzie zachodziło:
-- podobieństwo geometryczne - wymiary liniowe i kąty w pewnej skali będą takie same
-- podobieństwo kinematyczne - podobieństwo pół prędkości (spełniają warunek podobieństwa geometrycznego wektorowych pól prędkości)
-- podobieństwo dynamiczne - geometryczne podobieństwo wektorowych pól sił, wymaga identyczności liczb kryterialnych np. gdy przepływ jest opisany równaniami Naviera-Stokesa
=> podobieństwo dynamiczne jest spełnione, jeśli są spełnione warunki podobieństwa geometrycznego i kinematycznego.
=> ogólnie nie jest możliwe spełnienie wszystkich liczb kryterialnych podobieństwa dynamicznego; niektóre z nich wzajemnie się wykluczają. Stąd można mówić o podobieństwie zupełnym lub częściowym.
9. Krytyczna liczba Reynoldsa - rodzaje, wartości dla przepływów w rurociągach. Opisz rodzaje ruchu płynu korzystając z krytycznych liczb Reynoldsa. Podaj jednostki wielkości występujących we wzorze na Re.
![]()
Gdzie v0 - prędkość przepływu w przestrzeni pomiarowej [m/s]
d - średnica rury [m] ν - kinematyczny współczynnik lepkości przy danej temperaturze [m2/s]
Krytyczna liczba Reynoldsa jest miarą granicy podziału na przepływy laminarne i turbulentne, nie jest ona jednoznaczna i zależy od zaburzeń zakłócających przepływ w rurze.
W zależności od różnych czynników (drgania podłoża, dopływ wody z instalacji - woda nieuspokojona) przejście z przepływu laminarnego w turbulentny może zachodzić, gdy:
![]()
Rekrd<2300 - krytyczna dolna liczba Reynoldsa i przepływ jest zawsze laminarny
Rekrg>50000 - krytyczna górna liczba Reynoldsa i przepływ turbulentny
10. Wpływ charakteru opływu (laminarny i turbulentny) na ciała dobrze opływane.
W przypadku ciał dobrze opływanych, korzystnym jest jak najdłuższe utrzymanie przepływu laminarnego, podczas którego współczynnik oporu ciśnieniowego jest większy od współczynnika oporu tarcia. W momencie przejścia w przepływ turbulentny, wartość współczynnika tarcia może osiągnąć wartość równą lub nawet przewyższyć opór ciśnieniowy.
11. Wpływ charakteru opływu (laminarny i turbulentny) na ciała źle opływane.
W przypadku ciał źle opływanych(np. kula), podczas opływu laminarnego występuje duża różnica ciśnień (przed i za ciałem). Korzystnym jest zatem, utrzymanie przepływu turbulentnego, podczas którego współczynnik oporu ciśnieniowego ulega zmniejszeniu (różnica ciśnień i zawirowania maleją).
12. Opisz wpływ turbulencji strumienia w tunelu aerodynamicznym na Rekr opływu kuli.
W tunelach aerodynamicznych wartość Rekr opływu kuli jest unikalna dla każdego tunelu. Im większy stopień „nasycenia” drobnymi wirami (tunel o większej turbulencji przepływu), tym szybciej następuje przejście z opływu laminarnego do turbulentnego. Innymi słowy, liczna Reynoldsa szybciej osiąga wartość krytyczną.
13. Z jakich wzorów korzystamy przy obliczaniu parametrów przepływu w zwężce
Ventouriego.
Korzystamy z: -Równania Bernoulliego ![]()
; ponieważ z1=z2, równanie to przyjmuje postać ![]()
-Równania ciągłości ![]()
![]()
gdzie ![]()
; ![]()
są odpowiednimi przekrojami zwężki.
14. Na czym polega cechowanie zwężki Ventouriego?
Stanowisko do cechowania zwężki V. składa się z dwóch zwężek: badanej i wzorcowej. Znając wartości ciśnień w przekrojach zwężek, można obliczyć prędkości na wejściach do nich, a w konsekwencji współczynnik kv zwężki badanej. Wykorzystuje się przy tym fakt, że na wejściu do zwężki wzorcowej powinna być taka sama prędkość jak na wejściu do zwężki badanej.
![]()
15. Wzór na pomiar prędkości mierzonej drogą pomiaru ciśnień z pomocą rurki Prandtla.
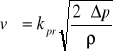
gdzie: kpr- współczynnik poprawkowy;
Δp=p0-p∞ różnica między ciśnieniem spiętrzenia a ciśnieniem w strumieniu niezaburzonym; ρ - gęstość płynu.
16. Definicja współczynnika oporu Cx.
Jest to liczba bezwymiarowa, wskazująca na proporcjonalność oporu do kwadratu prędkości, gęstości ośrodka i powierzchni odniesienia. Wartość współczynnika oporu zależy od kształtu ciała, jego usytuowania względem kierunku ruchu, od liczby Reynoldsa a przy dużych prędkościach również od liczby Macha.
![]()
gdzie![]()
-ciśnienie dynamiczne
R- siła oporu
17. Definicja wydatku masowego i objętościowego. Wzory.
Wydatkiem objętościowym przez powierzchnię S nazywamy objętość płynu przepływającego przez tę powierzchnię w jednostce czasu.
![]()
Wydatkiem masowym przez powierzchnię S nazywamy masę płynu przepływającego przez tę powierzchnię w jednostce czasu.
![]()
gdzie n -jest elementarnym wektorem normalnym do elementu powierzchni ds.
Dla płynu nieściśliwego, lub gdy powierzchnia dS jest niezbyt duża i można na niej przyjąć, że ρ= const
![]()
18. Interpretacja fizyczna liczby Reynoldsa.
Jest to stosunek sił bezwładności do sił tarcia wiskotycznego (lepkości)
19. Jakie skutki w pracy instalacji hydraulicznej (w rurach) wywołują straty przepływu?
Konsekwencją strat przepływu jest spadek ciśnienia całkowitego lub naporu całkowitego w instalacji hydraulicznej.
20. Rodzaje strat przepływu. Wzory na straty.
W zależności od przyczyn powodujących straty dzielimy je na:
-straty lokalne -wywołane zlokalizowanymi zmianami kształtu oraz wielkości i kierunku strumienia wywołującymi lokalną zmianę prędkości, której towarzyszy na ogół powstawanie wirów. Lokalny spadek naporu hydraulicznego określa się wg wzoru:
![]()
gdzie ξm- nazywa się współczyn strat lokalnych.
![]()
-straty tarcia -spowodowane nieodwracalnych zużyciem energii mechanicznej strumienia na pracę sił tarcia i zależą od prędkości przepływu i stosunku długości rury do średnicy jej przekroju wewnętrznego.
gdzie λ -współczynnik strat na tarcie, zależy od Re oraz względnej szorstkości.
21. Podaj interpretację fizyczną współczynnika Coriolisa.
Jest to stosunek rzeczywistej energii kinetycznej strumienia w pewnym przekroju poprzecznym do energii kinetycznej, obliczonej według prędkości średniej w tym przekroju.
22. Siły w płynach i ich podział.
W płynach nie mogą działać siły skupione na skutek braku sztywności postaciowej. Siły mogą działać w postaci związanych z masą płyną sił masowych i naprężeń, stąd podział na:
-siły masowe - są proporcjonalne do masy płynu (np. siła ciężkości, bezwładności);
-siły powierzchniowe -działają na powierzchnie elementu płynu w postaci naprężeń (np. ciśnienie).
Można też zastosować inny podział:
-siły wewnętrzne -będące wynikiem wzajemnego oddziaływania molekuł a mające charakter sił powierzchniowych, np. lepkość, siły adhezji i kohezji;
-siły zewnętrzne -których źródło znajduje się na zewnątrz rozpatrywanego elementu płynu
23. Podaj wzór na siłę oporu. Opisz wielkości występujące we wzorze. Podaj ich jednostki.
![]()
gdzie: CR -bezwymiarowy współczynnik;
-ciśnienie dynamiczne nieściśliwego strumienia niezaburzonego (nieskończenie daleko przed profilem) 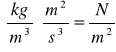
;
S- pole powierzchni charakterystycznej [m2].
![]()
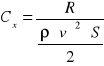
![]()
![]()
Wyszukiwarka