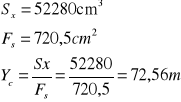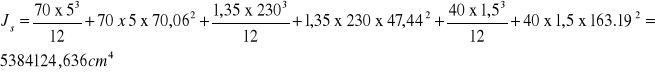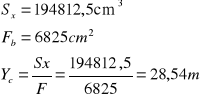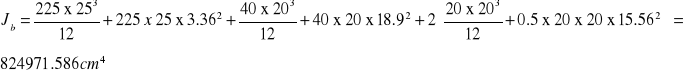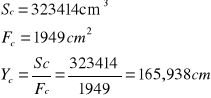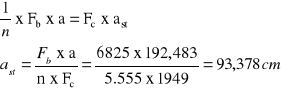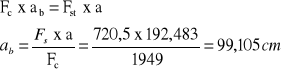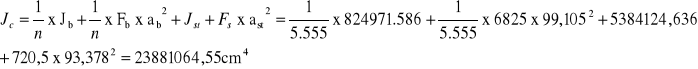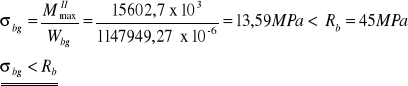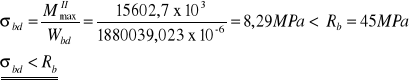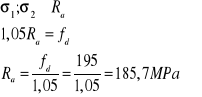Rok akad. 2008/2009
POLITECHNIKA KRAKOWSKA Wydział Inżynierii Lądowej Instytut Materiałów i Konstrukcji Budowlanych Katedra Budowy Mostów i Tuneli
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
TEMAT: „Projekt mostu zespolonego (stalowo - żelbetowego) kolejowego”
|
Uwagi:
Kraków, dnia 17.11.2007r. |
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 2 |
1) Opis techniczny
PRZEDMIOT PROJEKTU.
Przedmiotem opracowania jest projekt mostu zespolonego (stalowo - żelbetowego) kolejowego.
Podstawą opracowania jest: - temat ćwiczenia
Literatura: - PN-85/S-10030 - Obiekty mostowe - obciążenia - PN-82/S-10052 - Obiekty mostowe - konstrukcje stalowe - projektowanie - PN-91/S-10042 - Obiekty mostowe - konstrukcje betonowe, żelbetowe i sprężone, projektowanie
PRZEBIEG W PLANIE I PROFILU
Projektowany obiekt mostowy położony jest na prostoliniowym odcinku linii kolejowej. Przeszkodą na pokonanie której projektowany był obiekt jest rzeka spławna.
Kształtowanie przekroju poprzecznego obiektu mostowego, podyktowane jest charakterem linii kolejowej, która przeprowadzana jest po projektowanym obiekcie. Prowadzenie ruchu pociągów na obiekcie odbywa się w korycie balastowym-podsypkowym.
W zakres tego projektu wchodziło kształtowanie następujących elementów: - Blachownice - Płyta żelbetowa - Koryto balastowe z podsypką
PRZEKRÓJ PODŁUŻNY
Kształtowanie przekroju podłużnego obiektu mostowego, podyktowane jest charakterem przeszkody, której pokonanie jest celem obiektu oraz ukształtowaniem terenu. Znaczący wpływ ma tu rozpiętość teoretyczna obiektu .
Odwodnienie obiektu zapewnione jest dzięki odpowiedniemu pochyleniu (2%) płyty do wewnątrz, skąd przesączająca się przez warstwę podsypki i gromadząca się woda odprowadzana jest systemem rur do podpory obiektu i dalej do kanalizacji.
Projektowany obiekt mostowy zrealizowany został jako zespolony, złożony z blachownicy stalowej i żelbetowej płyty pomostowej. Materiał przewidziany do wykonania obiektu to beton B-60 i stal 18G2A. Dźwigar stalowy - blachownica projektowana jest w dwóch stanach pracy montażowym (wykonawczym) i stanie pracy użytkowej.
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 3 |
Wstępne wymiary projektowanego dźwigara stalowego: - Pas górny z blach o szerokości i grubości 40,0x1,5 cm - Pas dolny 70,0x5,0 cm - Środnik 230,0x 1,35 cm
Płyta pomostowa - żelbetowa wykonywana metodą tradycyjną w deskowaniach nieprzesuwnych. Grubość płyty zaprojektowano z koniecznym spadkiem od 25cm do 30cm, zbrojenie prętami wg rysunku. Wymiary dźwigara stalowego wstępnie przyjęto wg podanych zaleceń.
Dane i założenia projektowe.
- Klasa obciążenia kolejowego: k = 0 - Klasa betonu: B60 - Stal zbrojeniowa: St3SX-b - Stal konstrukcyjna: 18G2A - Rozpiętość teoretyczna:26,40m
2) Blachownica
Rozpiętość teoretyczna l = 26,40m Ciężar objętościowy stali: 78,5kN/m3 + dodatek do konstrukcji spawanych: 1,4kN/m3 Ciężar jednostkowy betonu w stanie suchym bez zbrojenia: 24kN/m3 + dodatek za zbrojenie 1kN/m3 +dodatek za wilgoć w betonie: 1kN/m3 `
Wysokość środnika belki (1/10 - 1/16)×26,40m = (2,64 - 1,65)
Przyjęto 1,60m
Grubość środnika Przyjęto grubość środnika tw=13mm Przyjęto grubość pasa górnego ts=16mm Przyjęto szerokość pasa górnego bs=200mm Szerokość pasa dolnego bf=450mm Przyjęto szerokość pasa dolnego bf-450mm Przyjęto grubość pasa dolnego tf=30mm(stal 18G2A)
2.2.) Zestawienie obciążeń stałych na jeden dźwigar
2.2.1) g1 - ciężar własny dźwigara
ciężar własny dźwigara (wartość charakterystyczna) :
G dźwigara = (0.2×0.016 + 0.45× 0.03 + 1.6× 0.013) ×( 78.5 + 1.4) = 2.996kN/m
ciężar własny dźwigara (wartość obliczeniowa)
G dźwigara = (0.2×0.016 + 0.45× 0.03 + 1.6× 0.013) ×( 78.5 + 1.4) ×1.2 = 3,595kN/m
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 4 |
Ciężar stężeń
Całkowity ciężar stężeń: 65.247 kN
Ciężar stężeń na 1mb dźwigara(wartość charakterystyczna:
Gstężeń =65.247 kN / 26,40m × 0.5 = 1.235kN/m
Ciężar stężeń na 1mb dźwigara(wartość obliczeniowa):
Gstężeń =65.247kN / 26,40m × 0.5 × 1.2 = 1.482kN/m
g 1 = G dźwigara + G stężeń = 3.595kN/m + 1.482kN/m = 5.077kN/m
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 5 |
2.2.2.) g2 - ciężar własny koryta balastowego
Pole powierzchni betonu w przekroju poprzecznym
F pł = 0,05 × 0,2 + (0,150 + 0,250) /2 × 0.850 + 0,850 × 0,280 + 2,250 × 0,25 + (0,800 + 0,400)/2 × 0,200 - 0,1 × 0,1 × 0,5 = 1,095m²
Ciężar koryta rozłożony na długości dźwigara (wartość charakterystyczna)
g 2 = F pł × ( γ b + γ z + γw ) = 1,095m²×( 24,0 + 1,0 + 1,0) = 28,47kN/m
Ciężar koryta równomiernie rozłożony na długości dźwigara (wartość obliczeniowa)
g 2 = F pł × ( γ b + γ z + γw ) × 1,2 = 1,095m²×( 24,0 + 1,0 + 1,0)×1,2 = 34,164kN/m
2.2.3) g2' - ciężar wilgoci zawartej w betonie
Ciężar wilgoci rozłożony na długości dźwigara (wartość charakterystyczna)
g 2 ٰ = F pł × γw = 1,095m²× 1,0 = 1,095kN/m
Ciężar wilgoci równomiernie rozłożony na długości dźwigara (wartość obliczeniowa)
g 2 ٰ = F pł × γw × 1,2 = 1,095m²× 1,0 × 1,2 = 1,314kN/m
2.2.4.) g3 - ciężar deskowania
Długość deskowanego obwodu (rozwiązanie systemowe ):
Udesk = 0,2+0,05+0,05+0,850+0,350+0,150+0,142+0,898+0,285+0,4+0,285+0,698 = 4,358m
Przyjęto grubość deskowania
Pole powierzchni deskowania w przekroju poprzecznym
Fdesk = Udesk × hdesk =4,358m × 0,05m = 0,218m²
Ciężar deskowania rozłożony na długości dźwigara (wartość charakterystyczna)
g 3 = F desk × ( γ desk + γ łącznik ) = 0,218m² × ( 6,0 + 2,7) = 1,896kN/m
Ciężar deskowania równomiernie rozłożony na długości dźwigara (wartość obliczeniowa)
g 3 = F desk × ( γ desk + γ łącznik ) × 1,2 = 0,218m² × ( 6,0 + 2,7) × 1,5 = 2,844kN/m
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 6 |
2.2.5.) g4 - ciężar warstw wyposażenia
2.2.5.1.) gprof - ciężar warstwy profilującej min. gr. 3cm
γ prof = 24,0kN/m³
Ciężar warstwy profilującej rozłożony na długości dźwigara (wartość charakterystyczna)
g prof = V prof × γ prof = 0,123m² × 24,0 = 2,97kN/m
Ciężar warstwy profilującej rozłożony na długości dźwigara (wartość obliczeniowa)
g prof = V prof × γ prof × 1,5 = 0,123m² × 24,0× 1,5 = 4,455kN/m
2.2.5.2.) gi - ciężar izolacji (2xpapa na lepiku) gr. 1cm
Ciężar izolacji rozłożony na długości dźwigara (wartość charakterystyczna)
g i = V i × γ i = ( 2,250 + 0,285 )×0,01 × 14,0 = 0,355kN/m
Ciężar izolacji równomiernie rozłożony na długości dźwigara (wartość obliczeniowa)
g i = V i × γ i × 1,5 = ( 2,250 + 0,285 )×0,01 × 14,0× 1,5 = 0,532kN/m
2.2.5.3.) gdoc - ciężar warstwy dociskowej z zaprawy cem-wap. gr. 5cm
Ciężar warstwy dociskowej rozłożony na długości dźwigara (wartość charakterystyczna)
g doc = V doc × γ doc = ( 2,200 + 0,266 )×0,05 × 24,0 = 2,959kN/m
Ciężar warstwy dociskowej rozłożony na długości dźwigara (wartość obliczeniowa)
g doc = V doc × γ doc × 1,5 = ( 2,200 + 0,266 )×0,05 × 24,0× 1,5 = 4,438kN/m
2.2.5.4.) gt - ciężar warstwy tłucznia
Średnia grubość warstwy tłucznia h tł = (0,500 + 0,466)/2 = 0,483m
Ciężar tłucznia rozłożony na długości dźwigara (wartość charakterystyczna)
g tł = V tł × γ tł = 2,200 ×0,483 × 20,0 = 21,252kN/m
Ciężar tłucznia równomiernie rozłożony na długości dźwigara (wartość obliczeniowa)
g tł = V tł × γ tł × 1,5 = 2,200 ×0,483 × 20,0 × 1,5 = 31,878kN/m
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 7 |
2.2.5.5.) gp - ciężar podkładów
Ciężar podkładów rozłożony na długości dźwigara (wartość charakterystyczna)
Ciężar podkładów równomiernie rozłożony na długości dźwigara (wartość obliczeniowa)
2.2.5.6.) gs60 - ciężar szyn S60
Ciężar szyn S60 rozłożony na długości dźwigara (wartość charakterystyczna)
Ciężar szyn S60 równomiernie rozłożony na długości dźwigara (wartość obliczeniowa)
2.2.5.7.) gs49 - ciężar szyn S49
Ciężar szyn S49 rozłożony na długości dźwigara (wartość charakterystyczna)
Ciężar szyn S49 równomiernie rozłożony na długości dźwigara (wartość obliczeniowa)
2.2.5.8.) gb - ciężar barierki
γ b = 0,5kN/m
Ciężar barierki rozłożony na długości dźwigara (wartość charakterystyczna)
g b = 1 × γ b = 1 ×0,5 = 0,5kN/
Ciężar barierki równomiernie rozłożony na długości dźwigara (wartość obliczeniowa)
g b = 1 × γ b × 1,5= 1 ×0,5 × 1,5 = 0,75kN/m
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 8 |
2.2.5.9.) gb - ciężar odwodnienia
γ odw = 0,25kN/m
Ciężar odwodnienia rozłożony na długości dźwigara (wartość charakterystyczna)
g odw = 1 × γ odw = 1 ×0,25 = 0,25kN/
Ciężar odwodnienia równomiernie rozłożony na długości dźwigara (wartość obliczeniowa)
g odw = 1 × γ odw × 1,5= 1 ×0,25 × 1,5 = 0,375kN/m
Zestawienie obciążeń dla jednej blachownicy
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 9 |
2.3.) Zestawienie obciążeń zmiennych na 1 dźwigar
2.3.1.) Obciążenie przyłożone w osi obiektu
α +k = 1.1³ dla klasy obciążenia „+3” α +k = 1.331
Gdy h>50cm stosujemy współ. Redukcyjny φ(h) h=60cm
P = 250kN × 1.5 × 1.331 × 1,102 = 550,035kN
p = 80kN/m × γ f × α k × φ = 80 × 1.5 × 1.331 × 1,102 = 176,011kN/m
2.3.2.) Obciążenia na 1 dźwigar
P = 250kN × 1.5 × 1.331 × 1,102× 0.5 = 275,017kN
p = 80kN/m × γ f × α k × φ = 80 × 1.5 × 1.331 × 1,102× 0.5 = 89,505kN/m
2.4.) Zestawienie obciążeń przy wykolejeniu
2.4.1.) przypadek I
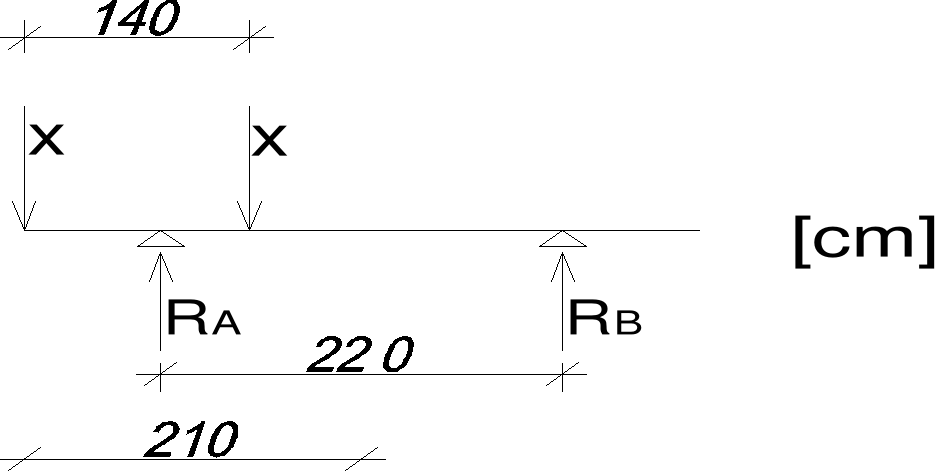
∑M A = 0,85x - 0,55x + 2,2R B = 0 → R B = - 0,12x
∑Y = x + x - R A - R B = 0 → R A = 2,12x
Dla x=50 Pw = γ f × α k × R A = 1.15 × 1.331 × 2,12 × 50 = 162,248kN/m
Dla x=25 pw = γ f × α k × R A = 1.15 × 1.331 × 2,12 × 25 = 81,124kN/m
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 10 |
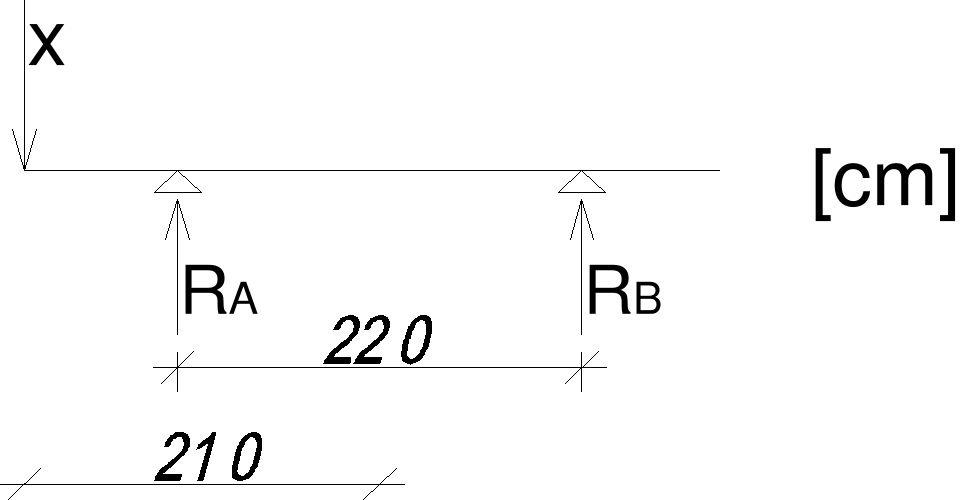
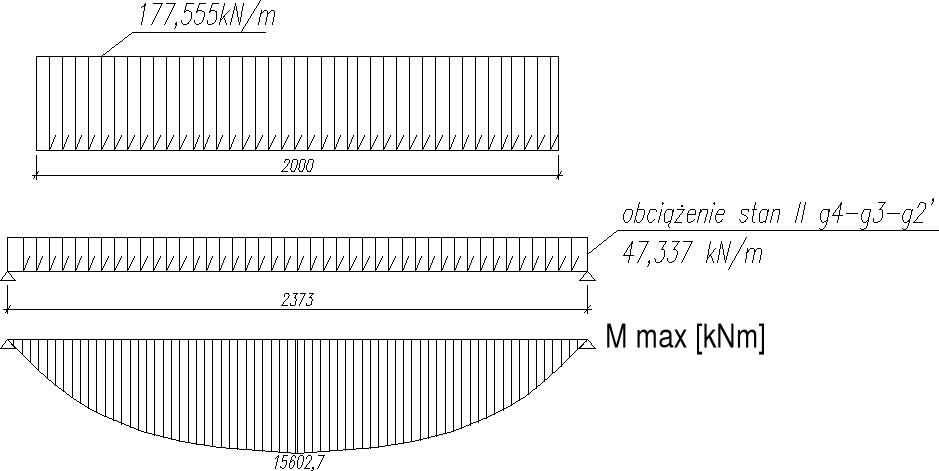
2.4.2.) Przypadek II
∑Y = x - R A - R B = 0 → R A = 1,45x
Dla x=80 Pw = γ f × α k × R A = 1.15 × 1.331 × 1,45 × 80 = 177,555kN/m
2.5.) Kombinacje obciążeń
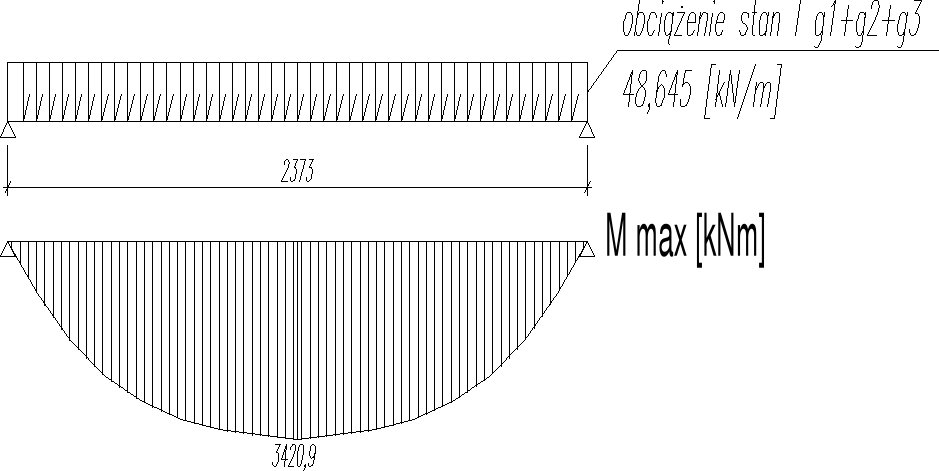
2.5.1.) Stan I - montażowy (g1+g2+g3)
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 11 |
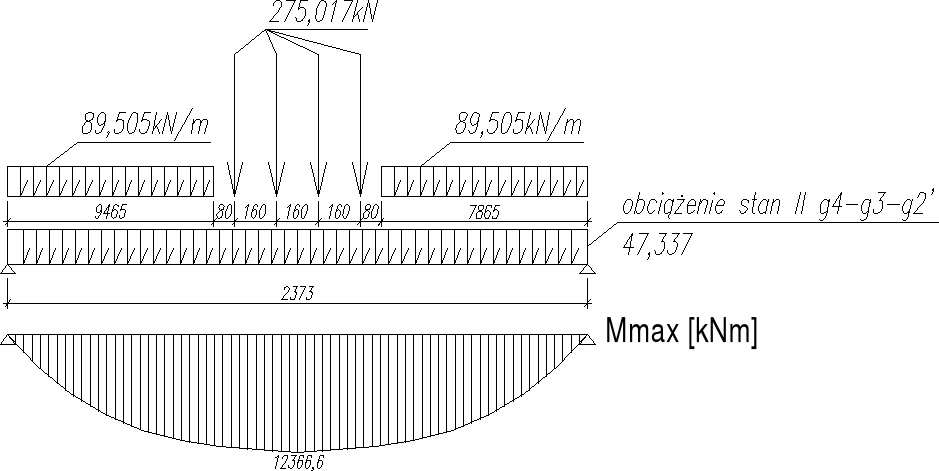
2.5.2.) Stan II - użytkowy (g4-g3-g2'+(p))
g3= (0,9/1,5) × 2,844 [kN/m] = 1.706 [kN/m]
g2'= (0,9/1,2) × 1,314 [kN/m] = 0,985 [kN/m]
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 12 |
2.5.3.) Stan przy wykolejeniu
2.5.3.1.) Stan I przy wykolejeniu
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 13 |
2.5.3.2.) Stan II przy wykolejeniu
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 14 |
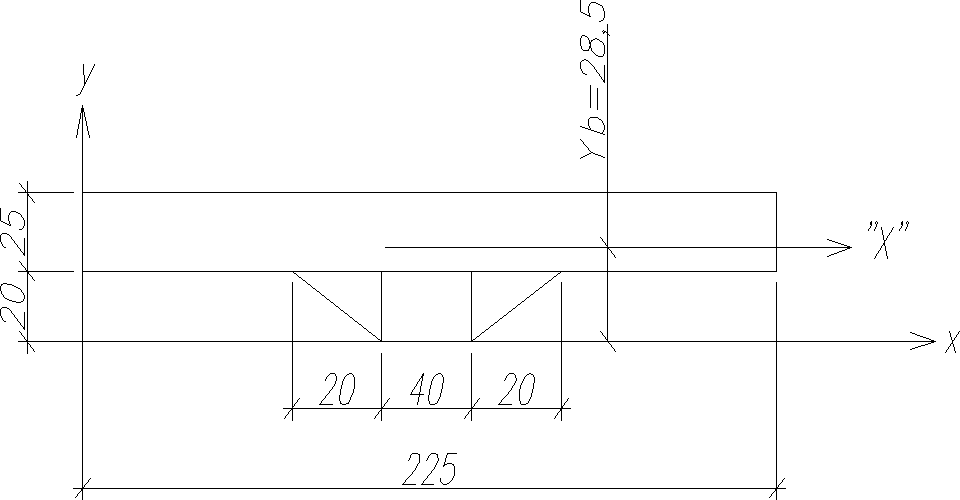
3) Charakterystyki geometryczne przekroju zespolonego
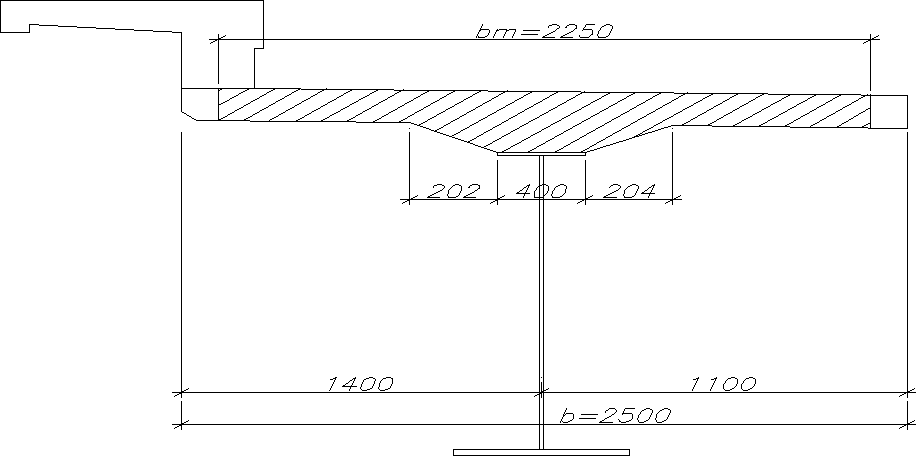
3.1.) Szerokość współpracująca płyty
L = 23.73m - rozpiętość mostu w osiach b = 2.5m - szerokość bm =0,9b szerokość współpracująca płyty wg.: Ryżyński A. i in.: „Mosty stalowe” bm=0,9x2,5=2,25m
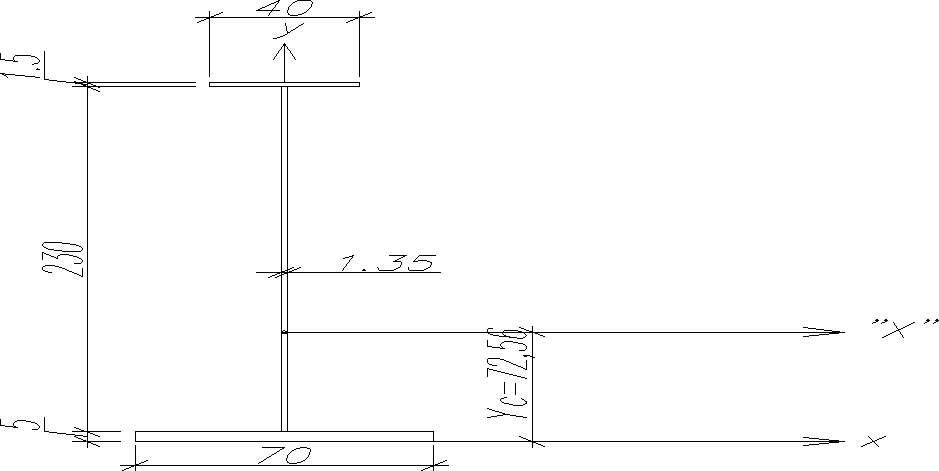
3.2.) Charakterystyki geometryczne przekroju dźwigara stalowego Pole przekroju
F s = 40×1,5 + 70× 5,0 + 2.3× 1,35 = 720,5cm²
Moment statyczny względem osi x
S x = 40×1,5 × 235,75 + 70× 5,0 × 2,5 + 230 × 1,35 × 120 = 52280cm³
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 15 |
Moment bezwładności dźwigara stalowego względem osi „X” przechodzącej przez jego środek ciężkości
3.3.) Charakterystyki geometryczne przekroju betonu współpracującego
Pole przekroju
F b =25 × 225 +(80 + 40)/2 × 20 = 6825cm²
Moment statyczny względem osi x
S x (80 + 40)/2 × 20× 10 + 225 × 25 × 325 = 194812,5m³
Moment bezwładności płyty betonowej względem osi „X” przechodzącej przez jej środek ciężkości
3.4.) Charakterystyki geometryczne przekroju zespolonego
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 16 |
Moment statyczny względem osi x dla całego przekroju
Moment bezwładności przekroju poprzecznego zespolonego względem osi x przechodzącej przez jego środek ciężkości (C)
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 17 |
Obliczenie wskaźników wytrzymałości
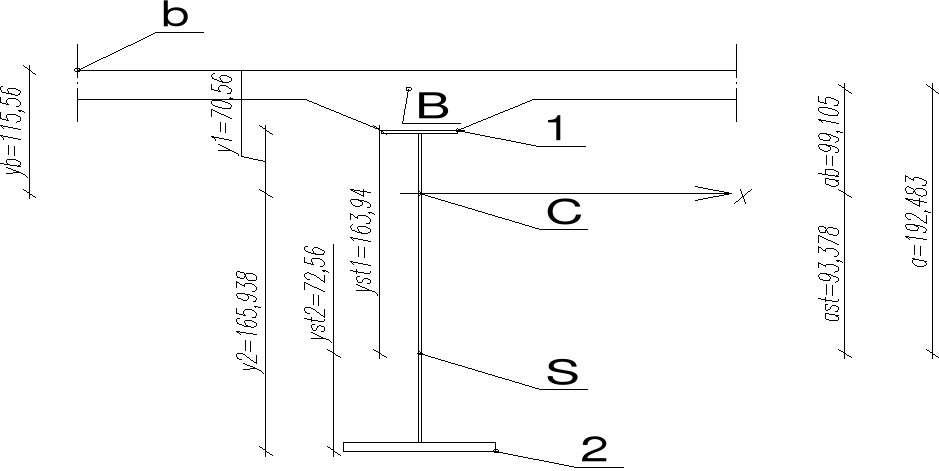
Ybg = 115,562cm - odległość środka ciężkości przekroju zespolonego od górnej powierzchni płyty betonowej
Ybd = 70,562cm - odległość środka ciężkości przekroju zespolonego od górnej powierzchni płyty betonowej
Y1 = 70,562cm - odległość środka ciężkości przekroju zespolonego od górnej powierzchni górnego pasa blachownicy
Y2 = 165,938cm - odległość środka ciężkości przekroju zespolonego od dolnej powierzchni dolnego pasa blachownicy
Wskaźniki wytrzymałości dla przekroju stalowego
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 18 |
4) Naprężenia
4.1.) Naprężenia normalne w betonie
Na krawędzi górnej:
Na krawędzi dolnej:
4.2.) Naprężenia normalne w stali
|
||
Mariusz ŻUROWICZ
Paweł KWATER gr. 511 |
PROJEKT Z PRZEDMIOTU KONSTRUKCJE MOSTOWE
|
str. 19 |
4.3.) Naprężenia normalne w stali w fazie I
Wartości naprężeń dopuszczalnych zostały nie przekroczone, a więc wymiary zostały dobrane poprawnie
|
||
Nazwa elementu |
Ilość w jednym przęśle |
Ilość w całym elemencie |
Wyrażenie |
Wynik [kN] |
Stężenia pionowe |
||||
L65x65x7 x2140 |
1 |
1x9 |
0,591kN/m x 2.14m x 1 x 9 |
11,38 |
L65x65x7 x2180 |
1 |
1x9 |
0,591kN/m x 2.18m x 1 x 9 |
11,6 |
Bl. 333x270x10 |
1 |
1x9 |
0,333x0,270x0,01x(78,5+1,4)x1x9 |
0,65 |
Wiatrownica w pasie dolnym |
||||
L65x65x7x2240 |
1 |
1x9 |
0,591x2,240x9 |
11,91 |
L65x65x7x2250 |
1 |
1x10 |
0,591x2,250x10 |
13.297 |
Żeberka pionowe |
|
|
|
|
Bl. 420x1270/2x1650x13 |
4 |
4x9 |
0,266×1,65×0,013×(78,5+1,4)×4×9 |
16,41 |
|
|
|
RAZEM: |
65.247 |
Obciążenia |
Składowa |
Ciężar (charakterystyczny) [kN/m] |
|
Ciężar (obliczeniowy) [kN/m] |
Razem (wart. char.) [kN/m] |
Razem (wart. obl.) [kN/m] |
g1 |
blachownica |
5,75 |
1,2 |
6,908 |
9,691 |
11,637 |
|
Stężenia |
3,941 |
1,2 |
4,729 |
|
|
g2 |
Koryto balastowe |
28,470 |
1,2 |
34,164 |
28,470 |
34,164 |
g2' |
Wilgoć z betonu |
1,095 |
1,2 |
1,314 |
1,095 |
1,314 |
g3 |
Deskowanie |
1,896 |
1,5 |
2.844 |
1,896 |
2.844 |
g4 |
Warstwa profilująca |
2,970 |
1,5 |
4,455 |
32,686 |
50,028 |
|
Izolacja |
0,355 |
1,5 |
1,532 |
|
|
|
Warstwa dociskowa |
2,959 |
1,5 |
4,438 |
|
|
|
Tłuczeń |
21,252 |
1,5 |
31,878 |
|
|
|
Podkłady |
0,800 |
1,5 |
1,200 |
|
|
|
Szyny S60 |
0,600 |
1,5 |
0,900 |
|
|
|
Szyna S49 |
0,500 |
1,5 |
0,750 |
|
|
|
Balustrada |
0,500 |
1,5 |
0,750 |
|
|
|
Odwodnienie |
0,250 |
1,5 |
0,375 |
|
|
|
Obc użytkowe |
2,5 |
1,5 |
3,75 |
|
|
Funkcja |
Tytuł zawodowy |
Imię i nazwisko |
Podpis |
Projektanci |
studenci |
Grzegorz Grabek
Marek Tuteja |
|
Weryfikator |
dr inż. |
Bogusław JAREK |
|
Wyszukiwarka