MATEMATYKA

SERIA 1

I. Ciągi liczbowe

Niech
. Otoczeniem liczby g nazywamy przedział
, gdzie
.

Definicja 1.

Mówimy, że liczba
jest granicą ciągu liczbowego
, co zapisujemy
, jeżeli dla każdego
istnieje taka liczba naturalna
, taka, że wyrazy ciągu
o wskaźnikach
spełniają nierówność
, co można zapisać w równoważnej postaci:
.

Zatem:
.

Uwaga. Sens powyższej definicji jest następujący: w dowolnym otoczeniu granicy g znajdują się „prawie wszystkie wyrazy ciągu
” tj. tylko skończona liczba wyrazów nie należy do otoczenia
.

Inaczej : wyrazy ciągu
„skupiają się” wokół liczby g .

Definicja 2.

Ciąg
, który ma skończoną granicę g nazywamy ciągiem zbieżnym , a granicę g nazywamy granicą właściwą.

Definicja 3.

Ciąg
, który nie ma granicy nazywamy ciągiem rozbieżnym.

Uwaga.

Jeżeli ciąg jest rozbieżny do
lub do
to
lub do
nazywamy granicą niewłaściwą.

Twierdzenie 1.

Ciąg zbieżny ma tylko jedną granicę (nie może mieć dwóch różnych granic).

Twierdzenie 2. (o granicach właściwych ciągów)

Jeżeli ciągi
są zbieżne do granic właściwych
,
, to

1.
,

2.
,
.

3.
.

4.
.

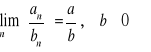
Twierdzenie 3. (o trzech ciągach)

Jeżeli ciągi
,
spełniają warunki:

1.
dla każdego
,

2
,

to
.

Wzory.

1.

2.

3.
.

4.
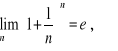
gdzie
,

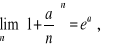
Przykłady.

1. Korzystając z definicji granicy ciągu udowodnić, że
.

Mamy pokazać, że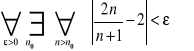
.

Niech
będzie dowolną liczbą dodatnią. Musimy znaleźć taką liczbę
taką, że dla każdego
spełniona będzie nierówność
.

Mamy

Zatem możemy przyjąć, że

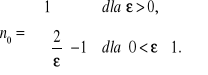
Symbol
oznacza tzw. część całkowitą liczby a , tj. największą liczbę całkowitą , która nie przekracza liczby a.

2.

.

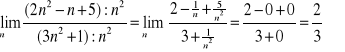
3. Obliczyć
.

Zauważmy najpierw, że dla każdego
mamy

.

Ponieważ
,
więc z twierdzenia o trzech ciągach otrzymujemy

.

4.
.

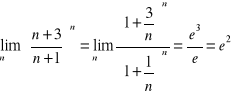
5.

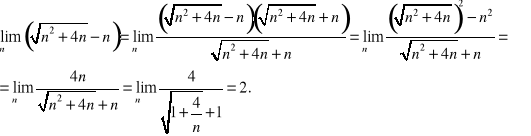
6.

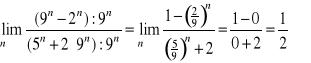
Zadanie 1.

1. Udowodnić , korzystając z definicji granicy ciągu , że :

.

2. Obliczyć granice następujących ciągów:

1)
; 2)
; 3)
;

4)
; 5)
, 6)
; 7)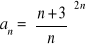
; 8)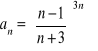
.

Odpowiedzi.

b) 1)
2)
3)
4)

5)
6)
7)
8)

Opracował: F. Bogowski

1

---