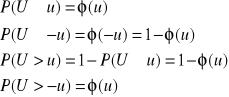1.Cechy statystyczne i ich rodzaje

- ilosciowe (skokowe, ciagle)

- jakosciowe

Cechy jakościowe (niemierzalne) to takie, których nie można jednoznacznie scharakteryzować za pomocą liczb (czyli nie można zmierzyć). Możemy je tylko opisać słowami. Możliwa jest zatem jedynie zupełna i rozłączna klasyfikacja zbioru wyników. Podstawową operacją pomiarową jest identyfikacja kategorii, do której należy zaliczyć wynik. Prowadzi to do podziału zbioru wyników na podzbiory rozłączne. Do cech jakościowych zaliczamy np. płeć, grupę krwi, kolor włosów, zgon lub przeżycie, stan uodpornienia przeciwko ospie (zaszczepiony lub nie) itp. W przypadku grupy krwi rezultat pomiaru będzie następujący: n1 pacjentów ma grupę krwi A, n2 pacjentów - grupę krwi B, n3 pacjentów - grupę AB i n4 - grupę O.

Cechy porządkowe umożliwiają porządkowanie (lub uszeregowanie) wszystkich elementów zbioru wyników. Cechy takie najlepiej określa się przymiotnikami i ich stopniowaniem. Każdemu ze stanów można również przypisać liczbę według wzrostu natężenia. Proces ten nazywa się rangowaniem. Na przykład, badając wzrost osoby, możemy użyć określeń: "niski", "średni" lub "wysoki". Podobnie, badając liczbę krwinek białych i używając określeń "poniżej normy", "w normie" lub "powyżej normy" - mamy do czynienia ze skalą porządkową.

Cechy ilościowe (mierzalne) to takie, które dadzą się wyrazić za pomocą jednostek miary w pewnej skali. Cechami mierzalnymi są na przykład: wzrost (w cm), waga (w kg), stężenie hemoglobiny we krwi (w g/dl), wiek (w latach) itp. Wśród cech mierzalnych wyróżniamy dwie podgrupy: cechy ciągłe i cechy skokowe.

Cecha ciągła to zmienna, która może przyjmować każdą wartość z określonego skończonego przedziału liczbowego, np. wzrost, masa ciała czy temperatura.

Cechy skokowe mogą przyjmować wartości ze zbioru skończonego lub przeliczalnego (zwykle całkowite), na przykład: liczba łóżek w szpitalu, liczba krwinek białych w 1 ml krwi.

2. Rodzaje badań statystycznych

Podstawowym kryterium - podziału metod badań statystycznych jest liczba jednostek statystycznych objętych badaniem na podstawie tego kryterium wyróżnia się:

badania pełne

badania częściowe

szacunki statystyczne

Do badań pełnych zaliczamy:

- spis statystyczny

- rejestrację statystyczną

- sprawozdawczość statystyczną

Do badań częściowych zaliczamy:

- badania reprezentacyjne

- badania monograficzne

- badania ankietowe

3.Tablice i wykresy statystyczne

W postaci tablic najczęściej przedstawiamy rezultaty obserwacji statystycznej . Tablice statystyczne są liczbowym obrazem struktury badanej zbiorowości. Są formą statystycznego uporządkowania danych liczbowych w sposób umowny. Tablice statystyczne są zbiorem szeregów statystycznych. Dzielimy je na: proste i kombinowane. Tablica, która zawiera jeden szereg nazywamy tablicą prostą. Tablice kombinowane składają się z kilku szeregów, przy czym obejmują one jedną zbiorowość statystycznej scharakteryzowaną według dwóch lub więcej cech jednocześnie.

Zasadniczo każda tablica składa się z trzech części: tytuł i nr. Tablicy i informacje na temat budowy tablicy.

Budując tablice statystyczne należy zwrócić uwagę aby każda jej pozycja była zapełniona odpowiednią liczbą. Jeśli z pewnych przyczyn nie możemy wypełnić jakiejś pozycji liczbą, to w tym miejscu stawiamy jeden z następujących znaków umownych:

-kreska (-) która oznacza, że dane zjawisko nie występuje

-kropka (.) która oznacza brak informacji lub brak wiarygodnych informacji o danym zjawisku

-zero (0) które oznacza, że dane zjawisko występuje, ale w ilościach rzędu mniejszego od rzędu liczb podanych w tablicy

-wykrzyknik (!) obok liczby używany jest dla podkreślenia, że została ona zamieszczona w tablicy jako poprawniejsza w porównaniu z poprzednio ogłoszoną

-krzyżyk (#) który oznacza, że rubryka nie może być wypełniona ze względu na układ tablicy.

Pod tablicą umieszcza się uwagi i odsyłacze, które zawierają dodatkowe wyjaśnienia dotyczące poszczególnych informacji lub całości tablicy

4. Srednie klasyczne, pozycyjne...

Miary średnie pozwalają określić tendencję centralną. Służą do określania tej wartości zmiennej, wokół której kupiają się wszystkie pozostałe zmienne.

Podział średnich:

1. Średnie klasyczne.

2. Średnie pozycyjne.

Do średnich klasycznych zalicza się średnie:

1. arytmetyczną

2. geometryczną

3. harmoniczną.

KLASYCZNE:

Średnia arytmetyczna to suma wartości zmiennej wszystkich jednostek badanej zbiorowości podzielona przez liczbę tych jednostek:

Jeżeli wartości zmiennej występują z różną częstotliwością, wówczas wylicza się średnią arytmetyczną ważoną (wagami są liczebności odpowiadające poszczególnym wartościom):

W przypadku danych zgrupowanych w szereg rozdzielczy przedziałowy wzór na średnią arytmetyczną jest następujący:

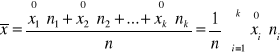
gdzie:

- środek i-tego przedziału klasowego

Średnia harmoniczna jest odwrotnością średniej arytmetycznej z odwrotności wartości zmiennych. W przypadku szeregów szczegółowych (wyliczających) średnią harmoniczną liczy się ze wzoru:

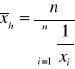
Średnią harmoniczną stosuje się wówczas, gdy wartości zmiennej podane są w jednostkach względnych

Średnia geometryczna jest pierwiastkiem n-tego stopnia z iloczynu n zmiennych:

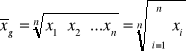
gdzie:

- znak iloczynu

Średnią geometryczną stosuje się w przypadkach, gdy wartości zmiennej tworzą postęp geometryczny lub w przypadku rozkładu skrajnie asymetrycznego.

Średnia ta ma zastosowanie przy badaniu średniego tempa zmian.

Średniej geometrycznej nie należy stosować, jeżeli którakolwiek z wartości zmiennej jest ujemna lub równa zeru!!!

POZYCYJNE:

Najczęściej wykorzystywanymi średnimi pozycyjnymi są: dominanta (moda, wartość najczęstsza) oraz mediana (wartość środkowa).

Dominantą nazywa się taką wartość zmiennej, nie będącą ani najmniejsza ani największą, która w danym rozkładzie empirycznym występuje najczęściej.

W szeregach rozdzielczych punktowych jest tą wartością cechy, której odpowiada największa liczebność.

W szeregach rozdzielczych przedziałowych bezpośrednio można wyznaczyć wyłącznie przedział zwany przedziałem dominanty (jest to przedział o największej liczebności).

Wartość dominanty wyznacza się ze wzoru:

gdzie:

- dominanta

- dolna granica przedziału dominanty

- liczebność przedziału dominanty

- liczebność przedziału poprzedzającego przedział

dominanty

- liczebność przedziału następującego po przedziale

dominanty

- interwał (rozpiętość) przedziału dominanty.

Dla szeregów rozdzielczych przedziałowych dominantę można również wyznaczyć metodą graficzną, która polega na wykreśleniu histogramu liczebności z trzech przedziałów klasowych: przedziału dominanty oraz dwóch przedziałów sąsiednich.

Wyznaczanie dominanty jest uzasadnione wówczas, gdy szereg spełnia następujące warunki:

• rozkład empiryczny jest rozkładem jednomodalnym,

• asymetria rozkładu jest umiarkowana,

• przedział dominanty i przedziały sąsiednie mają jednakowe rozpiętości

Medianą określa się taką wartość cechy, że co najmniej połowa jednostek ma wartość cechy nie większą niż i co najmniej połowa ma wartość nie mniejszą niż .

Medianą jest wartość cechy, którą posiada środkowa jednostka w uporządkowanym rosnąco ciągu elementów zbiorowości

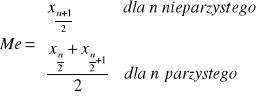
W przypadku szeregu rozdzielczego przedziałowego medianę wyznacza się metodą graficzną lub rachunkową. W metodzie graficznej wykorzystuje się wykres krzywej liczebności skumulowanej.

Jeżeli dane są przedstawione za pomocą szeregu rozdzielczego punktowego (cecha skokowa) - medianą jest pierwsza wartość, której odpowiada co najmniej połowa skumulowanej liczebności

Jeżeli mamy do czynienia z szeregiem rozdzielczym klasowym (dla cechy ciągłej) medianę można wyznaczyć wykorzystując wzór:

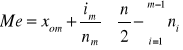
gdzie:

- liczebność i-tej klasy

- liczebność zbiorowości (próby)

- numer klasy zawierającej medianę

- dolna granica przedziału, w którym znajduje się

mediana

- interwał (rozpiętość) przedziału mediany

- liczebność przedziału mediany

5 Miary rozproszenia (dyspersji)

Na zjawiska masowe oddziałują dwa rodzaje przyczyn:

1. Główne (wywołujące zmienność systematyczną)

2. Uboczne (wywołujące zmienność przypadkową)

Przybliżonym miernikiem składnika systematycznego zbiorowości są miary przeciętne (średnie). Odchylenia wartości poszczególnych jednostek zbiorowości od wartości średniej powstają pod wpływem przyczyn przypadkowych (ubocznych).

Do pomiaru tych odchyleń wykorzystuje się miary zmienności (zróżnicowania, dyspersji, rozproszenia).

Dyspersja to zróżnicowanie jednostek badanej zbiorowości ze względu na wartość badanej cechy statystycznej. Siłę dyspersji można oceniać
za pomocą miar:

1. Klasycznych

2. Pozycyjnych.

Punktem odniesienia w miarach klasycznych jest średnia arytmetyczna, zaś miary pozycyjne wyznaczane są przede wszystkim na podstawie kwartyli.

Miary klasyczne:

1. Wariancja

2. Odchylenie standardowe

3. Odchylenie przeciętne (dewiata)

4. Współczynnik zmienności*.

* - jeśli do jego wyliczenia wykorzystywana jest średnia arytmetyczna oraz odchylenie standardowe)

Miary pozycyjne:

1. Empiryczny obszar zmienności (rozstęp, amplituda wahań, pole rozsiania)

2. Odchylenie ćwiartkowe

3. Współczynnik zmienności**.

** - jeśli do jego wyliczenia wykorzystywana jest mediana oraz odchylenie ćwiartkowe)

Najczęściej stosowane miary rozproszenia:

1. Obszar zmienności

2. Odchylenie przeciętne

3. Wariancja

4. Odchylenie standardowe

5. Współczynnik zmienności.

Obszarem zmienności określa się różnicę pomiędzy największą a najmniejszą wartością zmiennej, tzn.:

Miara ta ma niewielką wartość poznawczą, gdyż obszar zmienności uzależniony jest
od wartości skrajnych, które często różnią się istotnie od wszystkich pozostałych wartości zmiennej. Na obszar zmienności wpływają tylko wartości skrajne, pozostałe zaś nie mają żadnego wpływu na wynik. Obszar zmienności wykorzystywany jest jedynie przy wstępnej ocenie rozproszenia.

Odchyleniem przeciętnym d nazywa się średnią arytmetyczną z bezwzględnych odchyleń wartości zmiennej x od średniej arytmetycznej. Odchylenie przeciętne wyznaczamy z następujących wzorów:

• dla szeregu szczegółowego:

gdzie:

n - liczebność badanej zbiorowości

- wartości przyjmowane przez cechę mierzalną

- średnia arytmetyczna badanej zbiorowości

• dla szeregu rozdzielczego punktowego:

• dla szeregu rozdzielczego przedziałowego:

gdzie:

- środek i-tego przedziału klasowego

Wariancją określa się średnią arytmetyczną z sumy kwadratów odchyleń poszczególnych wartości cechy statystycznej od średniej arytmetycznej całej zbiorowości statystycznej. Wariancję wyznacza się z następujących wzorów:

- dla szeregu szczegółowego:

• dla szeregu rozdzielczego punktowego:

• dla szeregu rozdzielczego przedziałowego:

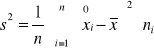
Podstawowe właściwości wariancji:

1. Jest zawsze liczbą nieujemną

2. Jest zawsze wielkością mianowaną, tzn. wyrażoną w jednostkach badanej cechy statystycznej. Miano wariancji zawsze jest kwadratem jednostki fizycznej, w jakiej mierzona jest badana cecha

3. Im zbiorowość statystyczna jest bardziej zróżnicowana, tym wartość wariancji jest wyższa

4. Wariancja, jako miara dyspersji wykorzystywana dla szeregów rozdzielczych przedziałowych, daje zawsze wartości zawyżone. Przyczyna zawyżenia wartości wynika z faktu, iż w przypadku szeregów rozdzielczych przedziałowych korzysta się ze środków przedziałów. W celu zmniejszenia popełnionego błędu, przy obliczaniu wariancji w przypadku przedziałów o zbyt dużej rozpiętości (i), stosuje się tzw. poprawkę Shepparda. Wzór na wariancję przyjmuje wówczas postać:

Odchylenie standardowe jest pierwiastkiem kwadratowym z wariancji

Odchylenie standardowe określa, o ile wszystkie jednostki statystyczne danej zbiorowości różnią się średnio od wartości średniej arytmetycznej badanej zmiennej

W statystyce odchylenie standardowe wykorzystywane jest do tworzenia typowego obszaru zmienności statystycznej. W obszarze takim mieści się około 2/3 wszystkich jednostek badanej zbiorowości statystycznej.

Typowy obszar zmienności określa wzór:

Użyteczność kategorii typowego obszaru zmienności sprowadza się przede wszystkim do rozdziału jednostek statystycznych
na typowe (tzn. występujące stosunkowo często) i nietypowe (tzn. występujące stosunkowo rzadko).

Z odchyleniem standardowym łączy się pojęcie zmiennej standaryzowanej (unormowanej) dla rozkładu empirycznego cechy mierzalnej :

Miary dyspersji (rozproszenia), jak i wartości średnie są liczbami mianowanymi. Fakt ten umożliwia bezpośrednie porównywania miar dyspersji obliczonych dla różnych szeregów.

Jeżeli badane zjawisko mierzone jest w różnych jednostkach miary lub kształtuje się na niejednakowym poziomie, wówczas do oceny rozproszenia należy stosować współczynnik zmienności.

Współczynnik zmienności jest ilorazem odchylenia przeciętnego lub odchylenia standardowego oraz średniej:

lub

(zamiast może być inna średnia, np. mediana)

Współczynnik zmienności może być wyrażony w procentach. Współczynnik ten zastępuje bezwzględne miary dyspersji

6.Miary asymetri i koncentracji

Szczegółowa analiza statystyczna powinna zawierać nie tylko poziom przeciętny i wewnętrzne zróżnicowanie zbiorowości. Istotne jest również określenie, czy przeważająca liczba jednostek znajduje się powyżej czy poniżej przeciętnego poziomu badanej cechy.

Należy dokonać zatem oceny asymetrii rozkładu. W związku z tym określa się charakter (kierunek) oraz natężenie (rozmiar) skośności.

W zjawiskach społeczno-gospodarczych zwykle spotyka się skośność dodatnią (prawostronną).

Skośność ta często występuje w badaniach:

• dochodów,

• wykonania norm pracy, planów pracy,

• absencji w pracy,

• wkładów oszczędnościowych,

• odległości przewozów osób, czy towarów.

Skośność dodatnia (prawostronna) ma miejsce wówczas, gdy dłuższe ramię krzywej charakteryzującej rozkład liczebności szeregu znajduje się po prawej stronie średniej.

Jeżeli dłuższe ramię krzywej znajduje się po lewej stronie średniej, wówczas można mówić o skośności ujemnej (lewostronnej).

Inaczej: jeśli spełniona jest nierówność:

to rozkład charakteryzuje się asymetrią prawostronną. Jeżeli natomiast:

to można wówczas mówić o asymetrii lewostronnej.

Charakter asymetrii można również określać na podstawie punktów wyznaczonych przez dominantę, medianę i średnią arytmetyczną.

W szeregu symetrycznym wszystkie miary pozycyjne są sobie równe.

W szeregu asymetrycznym miary te kształtują się na różnym poziomie: im większa skośność, tym większe są różnice pomiędzy dominantą, medianą i średnią arytmetyczną.

Jednym z mierników skośności jest wskaźnik skośności (inaczej: bezwzględna miara skośności):

Wskaźnik ten jest bezwzględną miarą asymetrii posiadającą miano badanej cechy. Z tego względu ma on ograniczone zastosowanie w analizie porównawczej. Poza tym, wskaźnik skośności określa jedynie kierunek asymetrii (prawo-, czy lewostronna) nie wskazując jej siły.

Miarą określającą zarówno kierunek jak i siłę asymetrii jest współczynnik skośności:

Współczynnik ten przyjmuje zazwyczaj wartości z przedziału: <-1;1>. Jedynie przy bardzo silnej asymetrii wartość współczynnika może wykroczyć poza w/w przedział

Jeżeli dany rozkład jest symetryczny, wówczas
.

W przypadku asymetrii prawostronnej:

.

Dla rozkładu o asymetrii lewostronnej:

.

Im silniejsza jest asymetria rozkładu, tym wartość bezwzględna współczynnika skośności jest wyższa.

7. Definicja prawdopodobieństwa

Prawdopodobieństwo to funkcja P(X), która przyporządkowuje każdemu elementowi zbioru zdarzeń losowych pewną nieujemną wartość rzeczywistą i ma następujące własności:

P(Ω) = 1, gdzie Ω jest przestrzenią zdarzeń elementarnych

prawdopodobieństwo sumy przeliczalnego zbioru zdarzeń parami rozłącznych jest równe sumie prawdopodobieństw tych zdarzeń:

P(A1 ∪ ... ∪ An ∪ ... ) = P(A1) + ... + P(An) + ...

8. Zmienna losowa

http://pl.wikipedia.org/wiki/Zmienna_losowa

http://pl.wikipedia.org/wiki/Funkcja_gęstości

9. Rozkład normalny, krzywa normalna

Rozkład zwany rozkładem Gaussa-Laplace'a jest najczęściej spotykanym rozkładem zmiennej losowej ciągłej.

Mówimy, że zmienna losowa ciągła X ma rozkład normalny o wartości oczekiwanej μ i odchyleniu standardowym σ

Rozkład prawdopodobieństwa w przypadku zmiennej losowej ciągłej nosi nazwę rozkładu (funkcji) gęstości

Funkcja gęstości w rozkładzie normalnym o postaci:

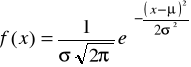
określona została dla wszystkich rzeczywistych wartości zmiennej X.

Funkcja gęstości w rozkładzie normalnym:

• jest symetryczna względem prostej x = ၭ

• w punkcie x = ၭ osiąga wartość maksymalną

• ramiona funkcji mają punkty przegięcia dla x = ၭ - σ

oraz x = ၭ + σ

• kształt funkcji gęstości zależy od wartości parametrów:

ၭ i σ. Parametr ၭ decyduje o przesunięciu krzywej,

natomiast parametr σ decyduje o „smukłości” krzywej

Prawdopodobieństwo w rozkładzie normalnym wyznacza się dla wartości zmiennej losowej z określonego przedziału

Natomiast:

W celu obliczenia prawdopodobieństwa zmiennej X w rozkładzie normalnym o dowolnej wartości oczekiwanej μ i odchyleniu standardowym σ dokonuje się standaryzacji

Standaryzacja polega na sprowadzeniu dowolnego rozkładu normalnego o danych parametrach ၭ i σ do rozkładu standaryzowanego (modelowego) o wartości oczekiwanej ၭ = 0 i odchyleniu standardowym σ = 1.

Zmienną losową X zastępujemy zmienną standaryzowaną U, która ma rozkład N(0,1)

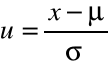
Zatem:

gdzie:

Wartości dystrybuanty standaryzowanego rozkładu normalnego - wartości te zostały stablicowane

Własności dystrybuanty standaryzowanego rozkładu normalnego:

10.. Własności rozkładu T studenta.

http://pl.wikipedia.org/wiki/Rozkład_Studenta

11. Estymacja parametru, własności dobrych estymatorów

Estymacja

Podstawowe pojęcia:

- parametr - charakterystyka określająca całą populację,

T_n - estymator - pewna funkcja określona na próbie, która służy do oszacowania nieznanej wartości parametru
,

T - ocena parametru
, jest to konkretna wartość liczbowa, którą przyjmuje estymator.

Estymator jest zmienną losową i ma pewien rozkład. Można obliczyć jego wartość oczekiwaną - E(T_n) i odchylenie standardowe - D(T_n) nazywane średnim błędem szacunku.

Własności estymatorów:

1. Nieobciążoność: E(T_n) =

odchylenia wartości estymatora od wartości parametru nie mają tendencyjnego charakteru (nie ma błędu systematycznego).

2. Zgodność:
dla dowolnego

wraz ze wzrostem liczby obserwacji wzrasta dokładność szacunku.

3. Efektywnością estymatora nieobciążonego T_n parametru
nazywamy iloraz:

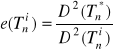
gdzie:
- oznacza estymator najefektywniejszy,
- to estymator badany.

Estymator jest najefektywniejszy jeżeli jest nieobciążony i ma najmniejszą wariancję.

Wyróżniamy estymację punktową i przedziałową.

Estymacja punktowa polega na tym, że za ocenę parametru przyjmuje się konkretną liczbę otrzymaną na podstawie próby losowej:

= T

zwykle dodajemy

= T
D(T_n)

Estymacja przedziałowa polega na tym, że konstruuje się pewien przedział (zwany przedziałem ufności), o którym możemy powiedzieć, iż z określonym prawdopodobieństwem 1-
pokryje wartość szacowanego parametru. Prawdopodobieństwo 1-
jest nazywane współczynnikiem ufności.

gdzie: k_d -jest to dolna granica przedziału, k_g - górna granica przedziału ufności.

Jeżeli estymator ma rozkład normalny to przedział ufności można zapisać w następujący sposób:

Na ćwiczeniach będziemy zajmowali się estymacją dla średniej (wartości oczekiwanej), wskaźnika struktury i wariancji.

12. Weryfikacja hipotez statystycznych

Testy istotności - jest to taki rodzaj testów, w których na podstawie wyników próby losowej podejmuje się jedynie decyzje odrzucenia hipotezy sprawdzanej lub stwierdza się, że brak jest podstaw do jej odrzucenia.

Wyróżniamy:

- parametryczne testy istotności (dotyczące wartości parametrów rozkładu)

- nieparametryczne testy istotności (pozostałe testy)

Parametryczne testy istotności:

test dla wartości średniej populacji generalnej, test dla dwóch średnich, test dla wskaźnika struktury (procentu), test dla dwóch wskaźników struktury, test dla wariancji, test dla dwóch wariancji.

Test dla wartości średniej (Przykładowe zadanie)

Zad 2.2, str. 61, Greń J., Statystyka matematyczna.

Zbadano w 81 wylosowanych zakładach pewnej gałęzi przemysłowej koszty materiałowe przy produkcji pewnego wyrobu i otrzymano średnią 540 zł oraz odchylenie standardowe 150 zł. Na poziomie istotności równym 0,05 zweryfikować hipotezę, że średnie koszty materiałowe przy produkcji tego wyrobu wynoszą 600 zł.

Dane:
= 540, s(x) = 150, n = 81,  = 0,05 - poziom istotności jest to prawdopodobieństwo popełnienia błędu I rodzaju, czyli odrzucenia hipotezy prawdziwej

Najpierw zapisujemy hipotezy:

H₀ : m = 600 (w hipotezie zerowej zawsze musi być równość)

H₁ : m
600 (w hipotezie alternatywnej:
,< , >)

Znak w hipotezie alternatywnej zależy od treści zadania. Jeżeli w treści zadania nie jest sprecyzowane, czy dany parametr ma być większy lub mniejszy od określonej wartości, to stawiamy zawsze znak
. Jeżeli w hipotezie alternatywnej występuje znak
to w teście występuje dwustronny obszar krytyczny. Gdy hipoteza alternatywna ma postać: < , > to stosujemy test z jednostronnym obszarem krytycznym. Znak > oznacza prawostronny, a znak < lewostronny obszar krytyczny.

Uwaga: Oznaczenia w hipotezach dotyczą populacji a nie próby, dlatego nie wolno zapisywać H₀ :
= 600

Ponieważ mamy dużą próbę i nie znamy odchylenia standardowego w populacji
obliczamy statystykę u:

m₀ - wartość którą weryfikujemy

Występuje dwustronny obszar krytyczny, Z tablic odczytujemy u_ (wartość krytyczna statystyki)

Jeżeli:
to odrzucamy H₀, na korzyść hipotezy alternatywnej, jeżeli
<
to nie ma podstaw do odrzucenia hipotezy H₀.  = 0,05 u_ = 1,96
= 3,6 > 1,96 = u_ odrzucamy H₀

Przy przyjętym poziomie istotności  = 0,05 odrzucamy H₀, czyli średnie koszty materiałowe przy produkcji tego wyrobu istotnie różnią się od 600 zł.

Nieparametryczne testy istotności

służą do sprawdzania hipotez nieparametrycznych (czyli takich, które nie dotyczą parametrów). Można podzielić na trzy zasadnicze grupy:

- testy zgodności

- testy losowości - weryfikujące hipotezę, że próba ma charakter losowy, np. test serii

- testy niezależności - sprawdzające hipotezę o niezależności dwóch zmiennych losowych, np. test niezależności
.

Testy zgodności można podzielić na dwie grupy:

1) testy służące do weryfikacji hipotez o postaci funkcyjnej rozkładu populacji generalnej (sprawdza się zgodność rozkładu empirycznego z próby z rozkładem hipotetycznym).

Wśród tych testów można wyróżnić grupę testów służących do weryfikacji hipotezy, że populacja generalna ma rozkład normalny. Są to testy normalności rozkładu, np. test Cramera - Smirnowa, Shapiro - Wilka.

2) testy służące do weryfikacji hipotez, że dystrybuanty dwóch lub więcej zmiennych losowych są identyczne (sprawdza się zgodność dwóch lub więcej rozkładów empirycznych z próby).

13 Korelacja

14. Pojecie szeregów czasowych.

---
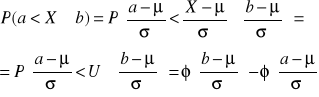