Abela Jeżeli szereg
jest zbieżny dla x=p≠0, to jest bezwzględnie zbieżny w przedziale (-|p|,|p|) i jednostajnie zbieżny w każdym przedziale domkniętym zawartym w przedziale (-|p|,|p|). Dowód szereg
jest zbieżny więc lim a_npⁿ=0, czyli
M> |a_npⁿ |≤M, stąd zaś mamy: |a_nxⁿ |=|a_npⁿ | |x/p|ⁿ≤Mqⁿ, jeśli tylko |x|≤q|p|. Szer. geometryczny
jest zbieżny dla q∈(0,1), zatem na mocy twierdzenia Weierstrassa, szereg
jest bezwzględnie i jednostajnie zbieżny w przedziale domkniętym [-q|p|,q|p|]⊂(-|p|,|p|). Zbieżność bezwzględna tego szeregu dla |x|<|p| wynika z kryterium porównawczego dla szeregów zbieżnych.

Ciągiem funkcyjnym nazywamy taki ciąg, którego wyrazami są funkcje f_n
R^A i który oznaczamy (f_n).

Ciąg Punktowo zbieżnym Ciąg (f_n) nazywamy pz do funkcji f na zbiorze A jeżeli:
A: lim f_n(x)=f(x). Zap
, Ciąg Jednostajnie zbieżny Ciąg (f_n) nazywamy jz do funkcji f na zbiorze A jeżeli:
, co zapisujemy
,

Cauchy'ego-Hadamarda Jeżeli istnieje różna od zera granica właściwa
, to promień zbieżności r szeregu potęgowego
jest równy r=1/μ.

Ciągłość funkcji Mówimy że odwzorowanie f: X→R, X
Rⁿ jest ciągłe w punkcie p₀
X gdy

Całka krzywoliniowa nieskierowana niech f będzie funkcją ograniczoną na łuku gładkim Γ, wtedy całkę krzywo niekierowaną z funkcji f po łuku Γ określamy wzorem:
, o ile granica po prawej stronie równości istnieje i nie zależy od sposobu podziału odcinka [α,β] ani od sposobu wyboru punktów P_k.

Całka powierzchniowa niezorientowana Jeżeli dla każdego normalnego ciągu podziałów D ciągu (s_n) ma granicę niezależną od wyboru punktów P_i, to granicę tę nazywamy całką powierzchniową niezorientowaną z funkcji g po płacie S i oznaczamy
, gdzie g: S→R, s_n=
, a P_i jest to dowolny punkt P_i (x_i, y_i, z_i)

Całką ogólną lub rozwiązaniem ogólnym równania różniczkowego n-tego rzędu nazywamy rodzinę funkcji postaci: y=y(x, c₁,…,c_n), która zależna jest od n stałych dowolnych, przy czym każda funkcja tej rodziny spełnia równanie. Poszczególne funkcje te rodziny przy ustalonych stałych nazywamy całką szczególną

Dirichleta Jeżeli funkcja f spełnia w przedziale [-T,T] warunki Dirichleta, to jest rozwijalna w tym przedziale w szereg trygonometryczny Fouriera i:
[-T,T]:f(x)=
. Jeżeli ponadto funkcja f jest okresowa i ma okres 2T, to równość ta jest prawdziwa dla każdego x z dziedziny tej funkcji.

Definicja Cauchy'ego: mówimy że odwzorowanie f: X→R, X
Rⁿ ma w punkcie p₀
X granicę q
B gdy


, gdzie d(p,p₀)=
,

Funk uwikłana jeżeli istnieje taka funkcja f: X→R, X
Rⁿ, że F(x₁,…,x_n, f(x₁,…,x_n))≡0 w X, to funkcję f nazywa

Grupa abelowa półgrupę unitarną, w której każdy element ma element symetryczny nazywamy grupą. Jeśli w grupie działanie jest przemienne, to nazywamy ja grupą abelową.

Kryterium Weierstrassa Jeżeli szereg Σ a_n jest szeregiem zbieżnym o wyrazach nieujemnych oraz
A: |f_n(x)|≤ a_n, to szereg funkcyjny Σ f_n jest jednostajnie zbieżny w zbiorze A.

O różniczkowaniu szeregu potęgowego Jeżeli promień zbieżności szeregu potęgowego
jest dodatni to suma s tego szeregu jest funkcją różniczkowalną i

oraz promień zbieżności szeregu pochodnych jest równy r.

O całkowaniu szeregu potęgowego jeżeli promień zbieżności r szeregu potęgowego
jest dodatni to suma s tego szeregu jest funkcją całkowalną w sensie Riemanna i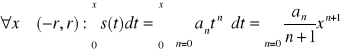
, oraz promień zbieżności szeregu całek jest równy r.

O rozwijaniu funkcji w szereg Taylora funkcja f∈C ^∞ (U(x₀,δ)) jest sumą swojego szeregu Taylora gdy
R_n(x)=0 w otoczeniu U, gdzie (R_n) jest ciągiem funkcyjnym o postaci
.

O jednoznaczności rozwinięcia funkcji w szereg Taylora jeżeli funkcja f jest w pewnym otoczeniu U(x₀,δ) sumą szeregu potęgowego
, to szereg ten jest szeregiem Taylora tej funkcji.

O różniczkowaniu funkcji złożonej Jeżeli funkcja f: X→R, jest różniczkowalna w obszarze X
Rⁿ a funkcje g_i:T→R, T
R^k, (i=1,…,n) mają pochodne względem zmiennych t₁,…,t_k, to funkcja złożona zmiennych t₁,…t_k ma w obszarze T pochodne cząstkowe względem tych zmiennych, które wyrażają się wzorami
……

O istnieniu funkcji uwikłanej Jeżeli funkcja F jest ciągła w otoczeniu punktu (x₀,u₀)
Rⁿ⁺¹ i ma w tym otoczeniu ciągłą pochodną F_u^', przy czym F(x₀,u₀)=0 i F_u^'(x₀,u₀)≠0, to istnieje takie otoczenie U₀ punktu (x₀,u₀), w którym równanie F(x,u)=0 posiada tylko jedno rozwiązanie u=f(x) będące funkcją ciągłą w pewnym otoczeniu punktu x₀, przy czym f(x₀)=u₀

O pochodnej funkcji uwikłanej Jeżeli funkcja F jest w otoczeniu punktu (x₀,u₀)
Rⁿ⁺¹ funkcją klasy C¹, przy czym F(x₀,u₀)=0 i F_u^'(x₀,u₀)≠0, to funkcja uwikłana u=f(x) określona równaniem f(x,u)=0 jest w pewnym otoczeniu U punktu x₀ funkcją klasy C¹ i: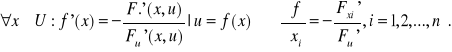

O istnieniu całki podwójnej (3) Jeżeli funkcja f: D→R jest ciągła w obszarze domkniętym D
R² (D
R³), to f jest całkowalna w tym obszarze.

O zamianie całki podwójnej na całki iterowane Jeżeli funkcja f: D→R jest ciągła w obszarze D
R² normalnym względem osi OX: D={(x,y)
R²: a≤x≤b ^φ(x)≤y≤ψ(x)},to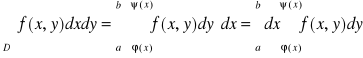
.

O zamianie całki 3 na całki iterowane (Fudiniego) Jeżeli funkcja f: V→R jest ciągła w obszarze V
R³ normalnym względem osi XOY: V={(x,y,z)
R³: (x,y)
D^φ(x,y)≤z≤ψ(x,y)},to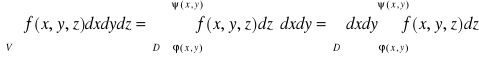

O zamianie zmiennych w całce podwójnej Jeżeli: 1. funkcja f: D→R jest ciągła w obszarze regularnym i domkniętym D
R², 2. odwzorowanie bijektywne ψ: Δ↔D określone równaniami: x=x(u,v) ^ y=y(u,v) jest klasy C¹(Δ), 3. jakobian J(u,v) odwzorowania ψ jest ograniczony i różny od 0 wewnątrz obszaru Δ, to zachodzi równość:

O zamianie zmiennych w całce 3 Jeżeli: 1. funkcja f: V→R jest ciągła w obszarze regularnym i domkniętym V
R³, 2. odwzorowanie bijektywne ψ: Ω↔V określone równaniami: x=x(u,v,w) ^ y=y(u,v,w) jest klasy C¹(Ω) ^ z=z(u,v,w), 3. jakobian J(u,v,w) odwzorowania ψ jest ograniczony i różny od 0 wewnątrz obszaru Ω, to zachodzi równość:

o zamianie całki krzywoliniowej nieskierowanej na całkę oznaczoną Jeżeli funkcja f jest ciągła na łuku gładkim Γ={(x(t), y(t)): t
[α,β], to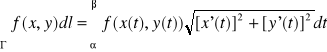
, jeżeli łuk dany jest w postaci jawnej Γ={(x,y): y=g(x), x
[a,b]}, to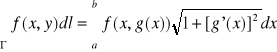
, postać biegunowa Γ: r=h(φ), φ
[a,b], to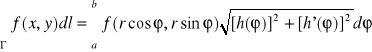
, Jeżeli łuk Γ i Γ={x=(x₁,x₂,…,x_n): x=Ф(t)=(φ₁(t),φ₂(t),… φ_n(t))}, to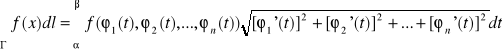

Promieniem zbieżności kres górny wartości bezwzględnych x, dla których szereg
jest zbieżny nazywamy (...) tego szeregu i oznaczamy przez r. Przedział (-r,r) nazywamy przedziałem zbieżności szeregu.

O zamianie całki powierzchniowej niezorientowanej na całkę podwójną Jeżeli funkcja g jest ciągła na płacie gładkim S={(z,y,z): z=f(x,y), (x,y)
D}, gdzie D
R² jest obszarem regularnym, to

Płatem zwykłym nazywamy homeomorficzny obraz obszaru płaskiego D, przy czym brzeg obszaru
D jest odwzorowany homeomorficznie na brzeg płata S. Jeżeli funkcje h_i
C¹(D), (i=1,2,3), to płat zwykły nazywamy płatem gładkim. Jeżeli ponadto w każdym punkcie obszaru D pochodna funkcji h=(h₁,h₂,h₃) jest różna od 0 to płat gładki nazywamy regularnym.

Różniczkowalność funkcję f określoną w pewnym otoczeniu U(x,δ) punktu x=(x₁, …,x_n) nazywamy różniczkowa w tym punkcie, jeżeli istnieją takie stałe a₁,…,a_n zależne tylko od x, że:
+
, gdzie Δx=(Δx1,…,Δxn),/Δx/=
, a o(/Δx/) jest tzw. nieskończenie małą rzędu wyższego niż /Δx/, tzn. taką funkcją, dla której lim(Δx→0)=o(|Δx|)/Δx=0,

Szeregiem funkcyjnym o wyrazach f_n nazywamy parę ciągów funkcyjnych ((f_n),(s_n)), gdzie s_n=
jest wyrazem ogólnym ciągu sum częściowych (s_n). Szereg funkcyjny ((f_n),(s_n)) oznaczamy symbolem Σ f_n.

Szeregiem zbieżnym punktowo (jednostajnie) Szereg Σ f_n, którego ciąg sum częściowych (s_n) jest zbieżny punktowo w zbiorze A nazywamy (...) w zbiorze A. Funkcję s, która jest granicą ciągu (s_n) nazywamy sumą punktową szeregu.

Szereg Taylora szereg potęgowy o środku w punkcie x₀ i współczynnikach c_n= f ⁽ⁿ⁾(x₀)/n! (n=1,2,...), gdzie f∈C ^∞ (U(x₀,δ)), nazywamy (...) funkcji f w tym otoczeniu. Jeżeli x=0 to taki szereg nazywamy szeregiem Maclaurina.

Szereg Fouriera szereg ortogonalny ∑c_nϕ_n, którego współczynniki określone są wzorami: c_n=(f,ϕ_n)/|| ϕ_n||², n=0,1,2... nazywamy (...) funkcji f.

Schwarza Jeżeli funkcja f: X→R, X
Rⁿ ma pochodne mieszane rzędu k i są one ciągłe w punkcie a
X, to te, które różnią się tylko kolejnością różniczkowań, są równe w tym punkcie.

Trajektorią ortogonalną Krzywą, która w każdym swoim punkcie tworzy kąt prosty z krzywą rodziny linii przechodzącą przez ten sam punkt, nazywamy (...) danej rodziny linii.

Taylora Jeżeli funkcja f: X→R, X
Rⁿ jest klasy C^k w obszarze X zawierającym odcinek I łączący punkty a i x, to: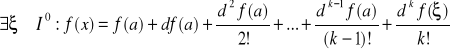
,

Teoria pola φ:R³→R-pole skalarne, F: R³→R³- pole wektorowe, gdzie F=[p(x,y,z), q(x,y,z), r(x,y,z)], grad: R→R³, φ→ grad φ=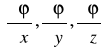
,div:R³→R,F→divF=
;rot:R³→R³,F→rotF=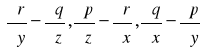
operator Hamiltona (nabla)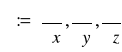
, grad φ=
φ, divF=
*F, rotF=
xF, bezźródłowe pole wektorowe F, dla którego divF=0, bezwirowe- dla którego rotF=0, Jeżeli istnieje pole skalarne φ takie że F=grad φ, to pole wektorowe nazywamy polem potencjalnym. Harmoniczne jednocześnie bezwirowe i bezźródłowe.

Układem ortogonalnym Ciąg funkcyjny (ϕ_n) o wyrazach ϕ_n ∈L²(a,b) nazywamy (...) funkcji jeżeli
(n≠k)⇒(ϕ_n,ϕ_k)=_a^b∫ϕ_n(x) ϕ_k(x)dx=0. Jeżeli ciąg (a_n) jest ciągiem liczbowym, zaś (ϕ_n) ciągiem ortogonalnym, to szereg funkcyjny ∑a_nϕ_n nazywamy szeregiem ortogonalnym, a wyrazy a_n współczynnikami tego szeregu.

Warunki Dirichleta Mówimy że funkcja f spełnia w przedziale [a,b] (...) jeżeli: 1. Funkcja f jest przedziałami monotoniczna w przedziale [a,b]. 2. funkcja f jest ciągła w przedziale [a,b], z wyjątkiem co najwyżej skończonej liczby punktów nieciągłości I rodzaju, przy czym w każdym takim punkcie x₀ mamy: f(x₀)=1/2 [f(x₀-)+f(x₀+)];

3. na końcach przedziału spełnione są równości: f(a)=f(b)=1/2 [f(a+)+f(a-)].

Warunek konieczny istnienia ekstremum (Fermata) Jeżeli funkcja f: X→R, X
Rⁿ jest różniczkowalna w punkcie a
X⁰ i w punkcie tym ma ekstremum lokalne, to f `(a)=0

Zastosowanie różniczki funkcji do obliczeń przybliżonych Jeżeli funkcja f ciągłe pochodne cząstkowe 1 rzędu w punkcie x₀,to: f(x₀+Δx)
f(x₀)+df(x₀,Δx), przy czym błąd tego przybliżenia dąży szybciej do 0 niż wyrażenie |Δx|,

Zagadnienie Cauchy'ego dla równania różniczkowego rzędu n: wyznaczyć rozwiązanie szczególne równania różniczkowego, które spełnia warunki początkowe: y(x₀)=y₀, y'(x₀)=y₁, …, y^(n-1)(x₀)=y_n-1 przy czym dowolne liczby rzeczywiste: x₀
I, y₀, y_1,..., y_n-1, zwane wartościami początkowymi są zadane z góry.

Zagadnienie Cauchy'ego dla równania liniowego n-tego rzędu: wyznaczyć całkę szczególną y spełniającą w przedziale (a,b) równanie (1) (lub(2)) i warunki początkowe: y(x₀)=y₀, y'(x₀)=y₁, : y^(n-1)(x₀)=y_n-1, gdzie x₀∈(a,b), y₀,y₁,...,y_n-1 - dowolne dane liczby.

Zastosowanie całek w fizyce Masa obiektu materialnego jeżeli ρ jest gęstością rozkładu masy to ∫ρ(x,y,z)dl=M, momenty statyczne M_Π=∫d*(P(x,y,z),Π)*ρ(x,y,z)dl, moment bezwładności B_Π= tak samo jak M tylko d do ², środek cieżkości x_c=M_y/M, y_c=M_x/M,

O rozwiązaniu ogólnym równania liniowego jednorodnego n-tego rzędu Jeżeli funkcje y₁,y₂,...,y_n tworzą fundamentalny układ rozwiązań równania y⁽ⁿ⁾+p_n-1(x)y^(n-1)+...+p₁(x)y'+p₀(x)y =0 w przedziale (a,b)⊂R, to kombinacja liniowa tych funkcji: y(x)=
z dowolnymi stałymi C₁,C₂,...,C_n jest rozwiązaniem ogólnym tego równania w rozważanym przedziale.

Całka Gaussa: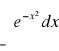
. Rozważymy całkę podwójną:
. Jeżeli obszar D jest kwadratem [-a,a]², to mamy równości:
=
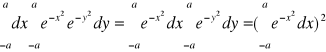
. Jeżeli obszar D jest kołem o promieniu b i o środku (0,0), to wprowadzając współrzędne biegunowe, otrzymamy: Δ: r∈[0,b), ϕ∈[0,2π),

=
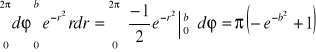
. K_a- koło o promieniu a i środku (0,0), K_R- koło o promieniu R i środku (0,0), Q-kwadrat [-a,a]². Z własności całki podwójnej mamy:

≤
,
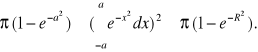
Przechodząc do granicy: a→+∞ (wtedy R→+∞), otrzymamy: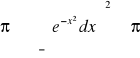
. Ostatecznie: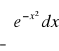
=
.

Warunek wystarczający istnienia ekstremum dla funkcji dwóch zmiennych Jeżeli w pewnym otoczeniu U punktu (x₀, y₀) funkcja F:U→R, U
Rⁿ spełnia warunki 1⁰ f
C²(U); 2⁰ f_x'(x₀, y₀)= f_y'(x₀, y₀)=0; 3⁰ det f `'(x₀, y₀) = f_xx''(x₀, y₀)* f_yy''(x₀, y₀)- (f_xy''(x₀, y₀))²>0, to funkcja f ma ekstremum w punkcie (x₀,y₀), przy czym: f_xx''(x₀, y₀)>0 => f(x₀, y₀)=
f(x,y); f_xx''(x₀, y₀)<0 => f(x₀, y₀)=
f(x,y). Jeżeli det f ”(x₀, y₀)<0, to funkcja f nie ma ekstrem.

Picarda o istnieniu i jednoznaczności rozwiązania zagadnienia Cauchy'ego. Jeżeli funkcja f spełnia warunki: 1. f:[x₀-a,x₀+a]x[y₀-b,y₀+b]→R jest ciągła; 2. f spełnia warunek Lipschitza:
[x₀-a,x₀+a]
y₁,y₂
[y₀-b,y₀+b]: |f(x,y₁)-f(x,y₂)|≤K*|y₁-y₂|, to istnieje taka liczba rzeczywista c>0, że w przedziale (x₀-c,x₀+c) równanie y'=f(x,y) posiada dokładnie jedno rozwiązanie spełniające warunek początkowy: y(x₀)=y₀.

Przegląd równań różniczkowych pierwszego rzędu. 1. Równanie o zmiennych rozdzielonych: y'=g(x)h(y). Ogólniej: A(x)B(y)dx+C(x)D(y)Dy=0. Piszemy równanie w postaci: Dy/dx=g(x)h(y)=> dy/h(y)=g(x)dx =>∫dy/h(y) =∫g(x)dx. Przypadek h(y)=0 badamy oddzielnie. 2 równanie jednorodne y'=f(y/x), Wprowadzamy nową funkcję niewiadomą u(x)=y(x)/x sprowadzamy to równanie do równania o zmiennych rozdzielonych. u=y/x =>y=xu => y'=u+xu'=>u+xu'=f(u) => x du/dx= f(u)-u => du/f(u)-u=dx/x 3. równanie postaci y'=f(ax+by+c),b≠0, podstawienie v(x)=ax+by(x)+c sprowadza to równanie do równania o zmiennych rozdzielonych.

4. równanie liniowe - równanie które można zapisać w postaci y'+p(x)y=g(x), nazywamy równaniem liniowym pierwszego rzędu. Jeśli g(x)=0 to równanie nazywamy równaniem liniowym jednorodnym. Będzie to wtedy równanie o zmiennych rozdzielonych. 1) etap rozwiązujemy równanie jednorodne. y'+p(x)y=0 => dy/dx= -p(x)y => dy/y= -p(x)dx =>ln|y|= -∫p(x)dx +ln|c| => y=ce^-∫p(x)dx - RORJ (rozw ogólne równ jednorod) 2) rozwiązanie ogólne wyznaczamy stosując M.U.S (metodę uzmienniania stałej). Przyjmujemy że rozwiązanie ogólne ma postać y(x)=c(x)e^-∫p(x)dx, y'(x)=c'(x)e^-∫p(x)dx + c(x)e^-∫p(x)dx(-p(x)) => y'+p(x)y=c'(x)e^-∫p(x)dx+c(x) e^-∫p(x)dx (-p(x))+ p(x)c(x)e^-∫p(x)dx=g(x) => c'(x)=g(x)e^∫p(x)dx =>c(x)=∫g(x)e^∫p(x)dx + C => y(x)=[∫g(x)e^∫p(x)dx+C]*e^-∫p(x)dx =>

y(x)=C e^-∫p(x)dx+ e^-∫p(x)dx *∫g(x)e^∫p(x)dx - RORNJ, 5. równanie bernoullie'ego y'+p(x)y=g(x)y^α, α≠0,α≠1, y=0 jest rozwiązaniem, gdy α>0, wyznaczamy rozwiązania niezerowe. Podstawiamy nowa funkcje niewiadomą o postaci

z=y^1-α, co sprowadza równanie do równania liniowego: z'=(y^1-α)'= (1-α)y ^-αy' =>y'/y^α=z'/1-α. Jeżeli zapiszemy równanie Bernuli'ego w postaci: y'/y^α +p(x)y^1-α=g(x) to otrzymamy równanie liniowe z funkcją niewiadomą z: z'/1-α +p(x)z=g(x).

6. Równanie różniczkowe zupełne. Równanie postaci P(x,y)dx+Q(x,y)dy=0 nazywamy równaniem zupełnym , jeżeli P,Q∈C¹(D) i lewa strona jest różniczką zupełną pewnej funkcji U(x,y), czyli gdy zachodzi warunek:
(x,y)∈ D:dP/dy=dQ/dx. Wtedy równanie można zapisać w postaci: dU=0, a więc rozwiązanie ogólne ma postać U(x,y)=C.

7. Równanie zupełne - czynnik całkujący. Jeżeli w równaniu P(x,y)dx+Q(x,y)dy=0 nie jest spełniony warunek
(x,y)∈D:dP/dy=dQ/dx., to szukamy takiej funkcji μ(x,y) klasy C¹ w obszarze D, aby dla równania: μ(x,y)P(x,y)dx+μ(x,y)Q(x,y)dy=0 spełniony był warunek:
(x,y)∈D:d(μP)/dy=d(μQ)/dx. Funkcję μ nazywamy czynnikiem całkującym danego równania. PRZYPADKI SZCZEGÓLNE 1. μ(x,y)=μ(x)

μ=μ(x); μ(x)P(x,y)dx+μ(x)Q(x,y)dy=0;
/
y (μ(x)P)=
/
x (μ(x)Q); μ(x)P_y'=μ'(x)Q+μ(x)Q_x';

μ(x)(P_y'- Q_x')=μ'(x)Q; μ'(x)/μ(x)= P_y'- Q_x'/Q. Czynnik całkujący zależy od zmiennej x i istnieje jeżeli P_y'- Q_x'/Q jest funkcja jednej zmie. x; ∫(μ'(x)/μ(x)) dx=∫ (P_y'- Q_x'/Q)dx ; ln|μ(x)|= ∫ (P_y'- Q_x'/Q)dx; ostat μ(x)=e^{∫ (Py'- Qx'/Q)dx},

2.μ(x,y)=μ(y); μ=μ(y); μ(y)P(x,y)dx+μ(y)Q(x,y)dy=0;
/
y (μ(y)P)=
/
x (μ(y)Q);

μ'(y)P(x,y)+ μ(y)P_y'= μ(y)Q_x'; μ'(y)P(x,y)= -μ(y)(P_y'- Q_x'); μ'(y)/μ(y)= P_y'- Q_x'/-P. Czynnik całkujący zależy od zmiennej y i istnieje jeżeli P_y'- Q_x'/-P jest funkcja jednej zmie. y; ∫(μ'(y)/μ(y)) dy=∫ (P_y'- Q_x'/-P)dy ;

ln|μ(y)|= ∫ (P_y'- Q_x'/-P)dy; ostat μ(y)=e^{∫ (Py'- Qx'/-P)dy},

8. Równanie Clairauta. y=xy'+ψ(y'), przy czym ψ(t)≠at+b i ψ∈C¹(I). różniczkujemy równanie y=xy'+ψ(y'), y'=1*y'+xy''+ψ'(y')y''; y''(x+ψ.'(y'))=0; 1) y”=0 v 2) x= -ψ.'(y'); 1) y”=0 => y'=A => y=Ax+B, wstawiamy do równania: Ax+B=xA+ψ(A)=>B=ψ(A); R.O. y=Ax+ψ(A); 2) x= -ψ.'(y'), podstawiamy y'=p i otrzymujemy postać parametryczną rozwiązania osobliwego {x= -ψ.'(p) ^ y= -ψ.'(p)*p+ψ(p)} to rozwiązanie jest obwiednią rodziny prostych, które otrzymaliśmy w rozwiązaniu ogólnym.

Równania różniczkowe rzędu 2 sprowadzalne do równań rzędu 1 - 1) Równanie w postaci F(x,y',y”)=0 - równanie nie zawiera funkcji niewiadomej. Podstawiamy u(x)=y' przez co sprowadzamy to równanie do rów rzędu 1: F(x,u,u')=0. 2) F(y,y',y”) - równanie nie zawiera zmiennej niezależnej x, podstawiamy y'=v(y), wtedy y”=v'v, a równanie przyjmuje postać: F(y,v,v'v)=0.

Równanie różniczkowe liniowe n-tego rzędu: (1) y⁽ⁿ⁾+p_n-1(x)y^(n-1)+...+p₁(x)y'+p₀(x)y=f(x), gdzie dane funkcje p_k (k=0,1,...,n-1) i f są ciągłe w przedziale (a,b)⊂R, nazywamy równaniem różniczkowym liniowym niejednorodnym n-tego rzędu. Jeśli f=0, to równanie to nazywamy równaniem liniowym jednorodnym n-tego rzędu:

(2) y⁽ⁿ⁾+p_n-1(x)y^(n-1)+...+p₁(x)y'+p₀(x)y =0.

Równanie liniowe jednorodne n-tego rzędu o stałych współczynnikach rzeczywistych.

(3) y⁽ⁿ⁾+a_n-1y^(n-1)+...+a₁y'+a₀y=0,
i=0,1,...,n-1: a_i=const. Poszukujemy rozwiązania tego równania w postaci: y(x)=e ^r.x. podstawiając do równania otrzymamy: (r ⁿ + a_n-1 r ^n-1+...+a₁r+a₀)e ^r.x=0. funkcja o postaci y(x)=e ^r.x jest rozwiązaniem równania jeżeli r spełnia równanie: r ⁿ + a_n-1 r ^n-1+...+a₁r+a₀=0, które nazywamy równaniem charakterystycznym. Struktura rozwiązań fundamentalnego układu równania zależy od pierwiastków R.CH. rozważamy 3 przypadki: 1) gdy R.CH ma n różnych pierwiastków rzeczywistych: r₁,r₂,...,r_n, r₁,r₂,...,r_n∈R, wtedy R.O przyjmuje postać y=C₁e^r.1.x+ C₂e^r.2.x+...+ C_ne^r.n.x, 2) gdy R.CH ma n różnych pierwiastków, wśród których mogą być pierwiastki zespolone - r₁=a+ib,r₂=a-ib, r₃....,r_n wtedy R.O -y=C₁e^a.xcos bx+ C₂e^a.xsin bx +... 3) R.CH ma pierwiastki wielokrotne. - r₁=r,r₂=r,...,r_k=r,r_k+1≠r.... wtedy R.O - y=C₁e^r..x+ C₂xe^r..x+...+ C_k x^k-1e^r.x,

Równania różniczkowe liniowe niejednorodne rzędu n. (1) p_n(x)y⁽ⁿ⁾+p_n-1(x)y^(n-1)+...+p₁(x)y'+p₀(x)y=f(x). Zakładamy że znane jest R.O równania jednorodnego: (2) p_n(x)y⁽ⁿ⁾+p_n-1(x)y^(n-1)+...+p₁(x)y'+p₀(x)y=0. możemy rozwiązywać dwiema metodami 1- M.U.S, 2- metoda przewidywania (tylko gdy p_i(x)=const)

1) Metoda uzmienniania stałej. Niech y₁,y₂,...,y_n będzie fundamentalnym układem rozwiązań równania (2), wtedy rozwiązanie ogólne tego równania ma postać: y(x)=C₁y₁(x)+ C₂y₂(x)+...+ C_ny_n(x). Zakładamy że rozwiązanie ogólne równania niejednorodnego (1) ma postać: y(x)=C₁(x)y₁(x)+ C₂(x) y₂(x)+...+ C_n(x)y_n(x), gdzie C₁,C₂,...,C_n są funkcjami które należy wyznaczyć. y'(x)=C₁'(x)y₁(x)+ C₂'(x) y₂(x)+...+ C_n'(x)y_n(x)+C₁(x)y₁'(x)+ C₂(x) y₂'(x)+...+ C_n(x)y_n'(x). układamy układ n równań na nieznane funkcje C₁,C₂,..,C_n : { C₁'(x)y₁(x)+ C₂'(x) y₂(x)+...+ C_n'(x)y_n(x)=0 ^ C₁'(x)y₁'(x)+ C₂'(x) y₂'(x)+...+ C_n'(x)y_n'(x)=0 ^....^ C₁'(x)_y1^(n-2)(x)+ C₂'(x) y₂^(n-2)(x)+...+

C_n'(x)y_n^(n-2)(x)=0 ^ C₁'(x)_y1^(n-1)(x)+ C₂'(x) y₂^(n-1)(x)+...+ C_n'(x)y_n^(n-1)(x)=f(x)/p_n(x)}, układ ten ma dokładnie jedno rozwiązanie ponieważ jest to układ cramerowski, jego wyznacznik główny(wrońskian) jest ≠0, stosując wzory Cramera otrzymamy: C_k'(x)=W_k/W, k=1,2,...,n. => C_k(x)=∫W_k/W dx +A_k, k=1,2,...,n.

2) Metoda przewidywania rozwiązania szczególnego - tą metodę stosujemy tylko do równań różniczkowych liniowych n-tego rzędu o stałych współczynnikach y⁽ⁿ⁾+a_n-1y^(n-1)+...+a₁y'+a₀y=f(x),
i=0,1,...,n-1: a_i=const., i tylko wtedy gdy funkcja f dana jest w postaci f(x)=e.^αx(W_i(x)cosβx + W_k(x)sinβx), gdzie i oraz k oznaczają stopień wielominu W. Rozpatrujemy 2 przypadki 1) y_s=e.^αx(W_m(x)cosβx + S_m(x)sinβx), gdy α+iβ nie jest pierwiastkiem W.CH tego równania. 2) y_s=x^p e.^αx(W_m(x)cosβx + S_m(x)sinβx), gdy α+iβ jest p-krotnym pierwiastkiem W.CH, przypadki szczególne 1) α=0, β=0 -f(x)=W_i(x), 2) β=0 - = e.^αx W_m(x), 3) α=0 - = (W_m(x)cosβx + S_m(x)sinβx),

Równanie Eulera n-tego rzędu a_nxⁿy⁽ⁿ⁾+a_n-1x^n-1y^(n-1)+...+a₁xy'+a₀y=f(x), rów Eulera jednorodne - =0, rozwiązujemy szukając rozwiązań o postaci: y=x^λ, y'=λ x^λ-1; y”= λ(λ-1) x^λ-2 ; y⁽ⁿ⁾= λ(λ-1)...(λ-n+1) x^λ-n. Wstawiając takie rozwiązanie do równania Eulera otrzymamy W.CH dla równania Eulera o postaci: a_nλ(λ-1)...(λ-n+1) x^λ-n+...+a₂λ(λ-1)+ a₁λ=0; gdy R.CH ma n różnych pierwiastków rzeczyw λ₁= a, λ₂=b...=>y=C₁x^a+C₂x^b+....

Gdy R.CH ma pier wielokrotne λ₁=λ, λ₂=λ..... =>y_s=C₁x^λ+ C₂x^λ ln x + C₃x^λ (ln x)²+..., gdy są pierw urojone λ₁=a+ib, λ₂=a-ib, ... y=C₁x^acos(b lnx)+ C₂x^asin(b lnx)+...

---