Ćwiczenie 5

Specyfikacja, estymacja i weryfikacja modelu - varia

1. Interpretacja parametrów strukturalnych w modelach liniowych względem parametrów:

(i)
, (ii)
,

(iii)
, (iv)
.

2. Konsekwencje przyjęcia założeń odnośnie do składnika losowego:
   ,
   ,
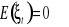
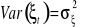
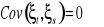
   dla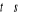
   oraz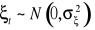
   . Dla postaci modelowych (i)-(iv) z pkt. 1 wyznacz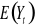
   ,
   ,
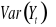
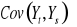
   dla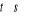
   oraz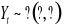
   . Zwróć szczególną uwagę na przypadek (iii).

Mamy dla niego:
. Stąd

.

Z uwagi na to, że
mamy
.

3. Modele z rozłożonymi opóźnieniami:

1. Opóźnione zmienne objaśniające

,
.

Rozwiązanie długookresowe:

Niech
oraz
, wówczas

- mnożnik długookresowy.

2. Opóźnienie (transformacja) Koycka

,
,
.

Mamy:
. Mnożymy powyższe obustronnie przez
a następnie odejmujemy od równia pierwszego i otrzymujemy:

lub
,

gdzie
.
- mnożnik długookresowy.

3. Opóźniona zmienna objaśniana:

Model częściowego dostosowania

, gdzie
- ,,pożądana” wielkość zmiennej objaśnianej, oraz

,
- równanie opisujące mechanizm dostosowawczy. Po podstawieniu równania pierwszego do drugiego otrzymamy

.

Model dostosowań adaptacyjnych

, gdzie:
- bieżąca wielkość zmiennej objaśniającej,
- ,,ocze-kiwana” wielkość zmiennej objaśniającej,
- wielkość krańcowa.

Zmiana oczekiwań:
,
. Stąd
. Z uwagi na to, że
mamy:

.

Mnożąc obustronnie przez
po przekształceniach otrzymamy

.

Ponadto:
oraz dla
,
i
dla wszystkich
(równowaga długookresowa),
i
.

4. Konsekwencje występowania w modelu opóźnionej zmiennej objaśniającej

,
. Jeśli
mamy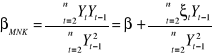
.
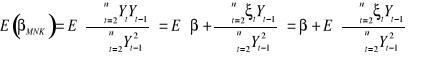
. Z uwagi na to, że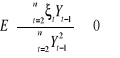

jest obciążonym estymatorem
. Niemniej jest estymatorem zgodnym (dlaczego?).

Dla
mamy:

,
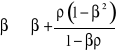
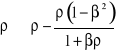
oraz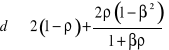
.

Wnioski: nawet w dużej próbie ocena
nie zbiega do prawdziwej wartości parametru w populacji, ocena
nie zbiega do prawdziwego
, ocena statystyki Durbina-Watsona nie zbiega do
.

1

---