Aleksandra Kral Wrocław 26.04.2005

127907

Termin zajęć:

Wtorek 15.15

Podstawy i algorytmy przetwarzania sygnałów

Ćwiczenie 2

Dyskretna Transformata Fouriera (DFT).

Prowadzący: prof. PWr dr hab. inż. Ryszard Makowski

1.Dyskretna transformata Fouriera dla przebiegu sinusoidalnego x = sin(2*pi*t*f).

Najpierw rozpatrzono przykład z całkowitą liczbą okresów.

Parametry:

N=248 - liczba próbek;

częstotliwość sygnału wynosi 64 Hz;

Przykład z niecałkowita liczbą okresów:

Parametry:

N=248 -liczba próbek;

częstotliwość sygnału wynosi 64 Hz;

W DFT sygnału okresowego zaobserwować można rozmycie widma-jest ono wyraźnie „rozciągnięte”.

2. Transformata sumy dwóch sinusoid.

Parametry:

-sinusoidy pierwszej:

N=256

f=48 Hz.

fp=1024

-sinusoidy drugiej:

N=256.

f=128 Hz.

fp=1024

Sinusoida pierwsza:

Sinusoida druga:

Suma sinusoid:

Można zauważyć ,że transformata sumy sygnałów sinusoidalnych jest równa sumie transformat poszczególnych sygnałów.

3. Składowa rzeczywista i urojona.

Badany sygnał to sinusoida postaci : x = sin(2*pi*t*f) i parametrach:

f =48 Hz

fp=1024

N=256

Składowa rzeczywista i urojona:

Składowa przeczywista przyjmuje wartości tylko dodatnie, a urojona także ujemne.

4.Wykres fazowy, rozwinięcie fazy.

Badanym sygnałem jest suma sinusa i obwiedni:

Można zauważyć ,że faza jest funkcją nieparzystą.

5. Widmo sygnału przesuniętego w czasie.

Badamy dwa sygnały : x1=sin(2*pi*t*f), x2=sin(2*pi*t*f+30*pi/4),gdzie:

f = 64;

fp = 1024;

N = 256;

Sygnały przesunięte w czasie, o fazie początkowej zero, mają taki sam moduł DFT ,ale różnią się w fazie.

6. Odwrotna dyskretna transformata Fouriera.

Badany sygnał : x= sin(2*pi*t*f), gdzie :

f = 64.

fp = 1024.

N = 256.

Znając transformatę sygnału można na jej podstawie odtworzyć sygnał oryginalny. Widać na wykresie, że amplituda widma jest taka sama jak amplituda sygnału, natomiast amplituda sygnału odtworzonego jest dużo mniejsza od amplitudy sygnału podstawowego

7. Badanie wybranych fonemów wyrazu z pliku plywak.wav.

Badanie fonemu „a” :

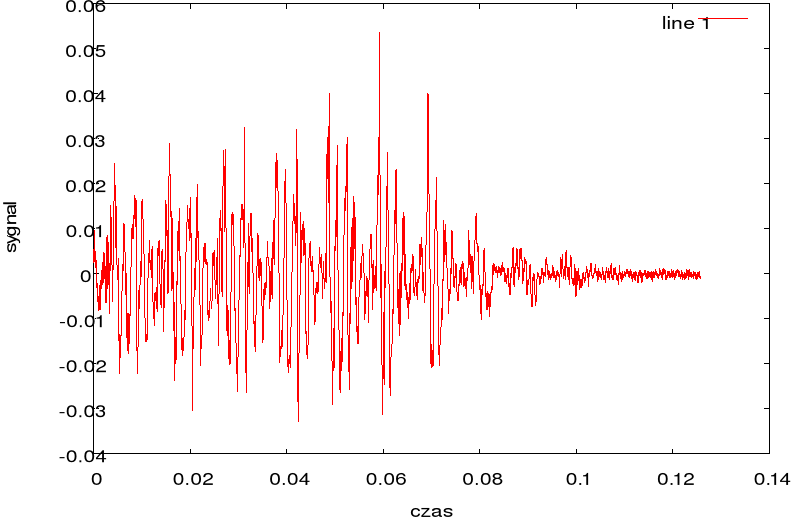
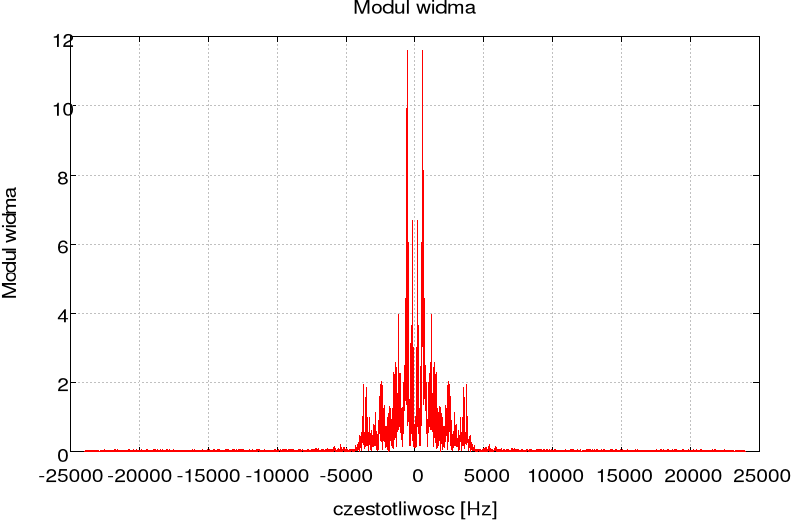
Widmo sygnału:

N=1024

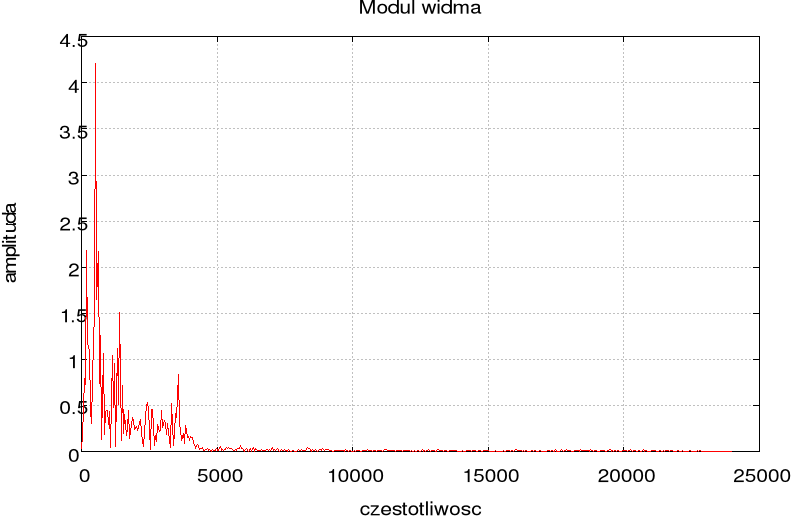
N=5500

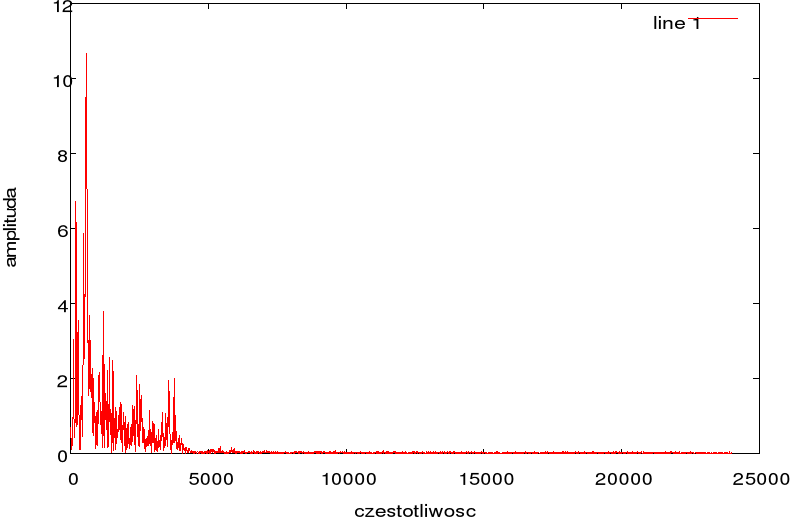
Transformata odwrotna:

N=1024

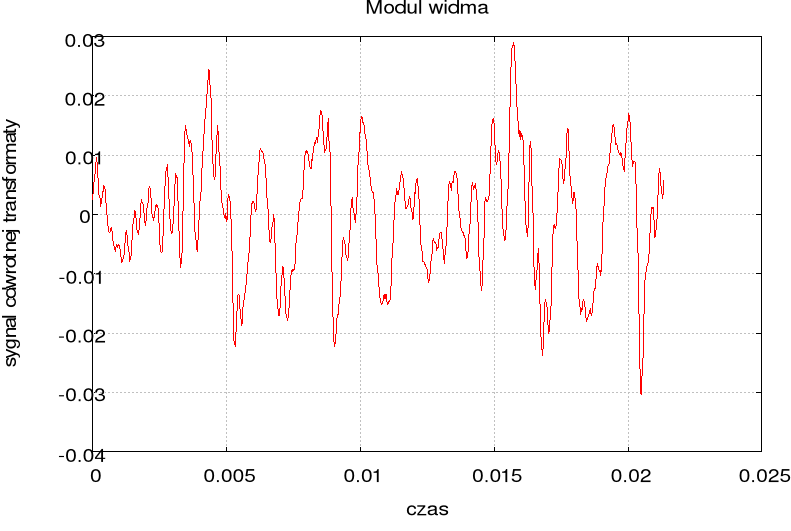
N=5500

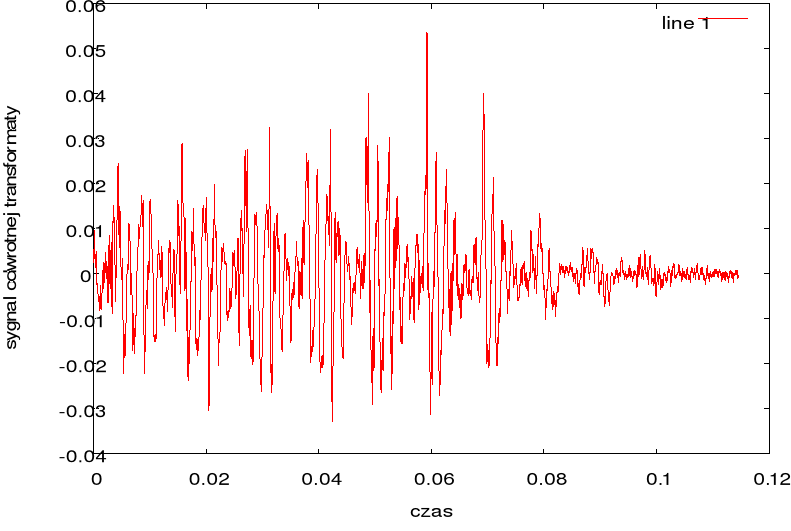
Moduł widma:

Znając transformatę sygnału można na jej podstawie odtworzyć sygnał oryginalny. Widać na wykresie, że amplituda widma jest taka sama jak amplituda sygnału, natomiast amplituda sygnału odtworzonego jest dużo mniejsza od amplitudy sygnału podstawowego

8.Wnioski:

8.1 W DFT sygnału okresowego zaobserwować można rozmycie widma-jest ono wyraźnie „rozciągnięte”.

8.2 Można zauważyć ,że transformata sumy sygnałów sinusoidalnych jest równa sumie transformat poszczególnych sygnałów.

8.3 Składowa rzeczywista przyjmuje wartości tylko dodatnie, a urojona także ujemne.

8.4 Faza jest funkcją nieparzystą.

8.5 Sygnały przesunięte w czasie, o fazie początkowej zero, mają taki sam moduł DFT ,ale różnią się w fazie.

8.6 Znając transformatę sygnału można na jej podstawie odtworzyć sygnał oryginalny. Widać na wykresie, że amplituda widma jest taka sama jak amplituda sygnału, natomiast amplituda sygnału odtworzonego jest dużo mniejsza od amplitudy sygnału podstawowego

8.7 Znając transformatę sygnału można na jej podstawie odtworzyć sygnał oryginalny. Amplituda widma jest taka sama jak amplituda sygnału, natomiast amplituda sygnału odtworzonego jest dużo mniejsza od amplitudy sygnału podstawowego

---