I PRACOWNIA FIZYCZNA U. ŚL.

nr ćwiczenia ........  .......... temat .δ σρ .

.. ≥σ ρ ≥ ......................................

imię i nazwisko .......... ρ  ..........................

rok studiów .....  ...... kierunek ......  .................

grupa ....  ...... data wykonania ćwiczenia ρ .

ZAGADNIENIA TEORETYCZNE DO DOŚWIADCZENIA NR 77

(badanie skręcenia płaszczyzny polaryzacji światła)

1. Polaryzacja światła.

Światło, podobnie jak każde promieniowanie elektromagnetyczne, jest falą poprzeczną. Kierunki drgań wektorów elektrycznych są prostopadłe do kierunku ruchu fali, a nie równoległe, jak ma to miejsce w przypadku fal podłużnych. Zazwyczaj światło jest falą bardzo złożoną, ponieważ występują równocześnie fale o różnych długościach, a drgania zachodzą we wszystkich płaszczyznach przechodzących przez kierunek rozchodzenia się. Celem uproszczenia często zakładamy, że mamy do czynienia ze światłem monochromatycznym, a także ograniczamy drgania fali świetlnej do tylko jednej płaszczyzny. Mówimy wtedy, że światło jest liniowo spolaryzowane. Płaszczyzną polaryzacji nazywamy płaszczyznę prostopadłą do płaszczyzny, w której zachodzą drgania. Równanie fali światła monochromatycznego o długości fali λ, spolaryzowanego liniowo w płaszczyźnie wyznaczonej kierunkami z, y przyjmuje postać:

2. Polaryzacja kołowa i eliptyczna.

Polaryzacja liniowa nie jest jedynym sposobem uporządkowania drgań świetlnych. Może również istnieć światło, w którym koniec wektora natężenia pola elektrycznego zakreśla linię śrubową wokół kierunku rozchodzenia się. Mówimy wtedy o polaryzacji kołowej (gdy E_y=E_x) lub eliptycznej (E_y≠E_x). Światło spolaryzowane kołowo lub eliptycznie można otrzymać przepuszczając światło spolaryzowane liniowo przez cienką płytkę wykonaną z kryształu optycznie czynnego. Światło na płytce rozpada się na wiązkę zwyczajną i nadzwyczajną. Jeżeli prędkości rozchodzenia się są różne dla obydwu wiązek powstaje różnica faz a wypadkowe drganie będzie drganiem eliptycznym, a ze względu na równoczesny ruch fali świetlnej w kierunku osi z falą spolaryzowaną kołowo lub eliptycznie.

3. Kąt Brewstera.

Światło odbite od dielektryka ulega polaryzacji w przypadku, gdy kąt padania jest równy kątowi Brewstera. Jeżeli płytkę oświetlamy światłem spolaryzowanym liniowo, to stan polaryzacji wiązki odbitej zależy od kąta β między płaszczyzną polaryzacji światła padającego i płaszczyzną padania. Gdy kąt β=0, światło odbite jest całkowicie spolaryzowane, gdy kąt β=90°, światło padające pod kątem Brewstera nie odbija się. Jeżeli odbije się światło spolaryzowane liniowo, to stan polaryzacji nie ulega zmianie tylko w przypadkach β=0 i β=90°. W innych przypadkach powstaje polaryzacja eliptyczna. Światło spolaryzowane liniowo rozłożyć można na składowe: równoległą i prostopadłą do płaszczyzny padania. Każda z tych składowych doznaje innego skoku fazy przy odbiciu. Stąd zmienia się faza między składowymi i w wyniku nałożenia się po odbiciu stan polaryzacji zmienia się na eliptyczny. Zgodnie ze wzorem współczynnika załamania dla kąta Brewstera otrzymujemy:

.

Gdy składowa równoległa dla kąta polaryzującego jest całkowicie załamana, a składowa prostopadła załamana tylko częściowo, wiązka jest tylko częściowo spolaryzowana.

4. Sposoby polaryzacji światła.

Podwójne załamanie - na skutek zjawiska podwójnego załamania światło ulega rozproszeniu na wiązki: zwyczajną i nadzwyczajną. W kryształach tzw. jednoosiowych istnieje kierunek zwany osią główną, w którym nie występuje podwójne załamanie. Oś główna wyznacza jedynie kierunek w krysztale, stąd każda linia równoległa jest również osią główną. Każdą płaszczyznę równoległą do osi głównej nazywamy przecięciem głównym. Przekrojem głównym nazywamy płaszczyznę wyznaczoną przez promień padający i oś główną. Promień zwyczajny jest spolaryzowany w płaszczyźnie prostopadłej do płaszczyzny przekroju głównego. Kąt jaki tworzą wiązki zwyczajna i nadzwyczajna jest zazwyczaj niewielki. Chcąc uzyskać światło spolaryzowane jedną z tych wiązek należy wyeliminować. W tym celu stosuje się pryzmat Nicola (nikol) usuwający jedną z wiązek. Nikol jest pryzmatem ze szpatu islandzkiego (CaCO₃ - minerał w formie kryształów) składającym się z dwóch części. Powierzchnie przecięcia sklejone są na powrót balsamem kanadyjskim o współczynniku załamania n=1,55. Tymczasem współczynniki załamania szpatu wynoszą: dla promienia zwyczajnego n_z=1,66, a dla nadzwyczajnego n_n=1,49. Tak więc dla promienia zwyczajnego warstwa balsamu kanadyjskiego stanowi środowisko optycznie rzadsze, a dla nadzwyczajnego optycznie gęstsze. Kąty w pryzmacie dobrane są w taki sposób, że promień zwyczajny pada na warstwę balsamu pod kątem większym od granicznego, wobec czego ulega całkowitemu wewnętrznemu odbiciu. Promień zwyczajny wychodzi przez boczne ścianki pryzmatu i zostaje pochłonięty przez czarną powierzchnię obudowy. Promień nadzwyczajny przechodzi doznając tylko niewielkiego przesunięcia równoległego. Ponieważ każdy z promieni jest spolaryzowany liniowo, światło przechodzące przez nikol jest spolaryzowane liniowo w płaszczyźnie prostopadłej do przecięcia głównego.

Polaryzacja przez odbicie - Jeżeli kąt padania dobrany jest tak, by kąt między promieniem odbitym a załamanym wynosił 90°, wtedy promień odbity jest całkowicie liniowo spolaryzowany w płaszczyźnie padania, a promień załamany spolaryzowany jest częściowo w płaszczyźnie prostopadłej do płaszczyzny padania. Zjawisko to jest wykorzystywane do polaryzacji światła. Chcąc uzyskać całkowitą polaryzację światła załamanego musimy przepuścić je przez wiele równoległych płytek załamujących.

Polaryzacja przez dichroizm - do uzyskania światła spolaryzowanego bardzo często wykorzystuje się tzw. zjawisko dichroizmu kryształów. Światło przechodzące przez kryształy jest częściowo pochłaniane. Kryształy dichroiczne wykazują różnicę współczynników pochłaniania promieni zwyczajnego i nadzwyczajnego. W szczególności należy do nich Turmalin pochłaniający silne promienie zwyczajne biegnące wzdłuż osi optycznej. Turmalin nie jest jednak wygodny, ponieważ silnie osłabia światło, a współczynniki załamania zależą od długości fali. Lepiej do tego celu nadają się kryształy heparytu (sól siarczana jodochininy), które już przy grubości rzędu 0,3mm pochłaniają całkowicie jeden z promieni. Płytki heparytowe nazywamy polaroidami; wytwarzać je można na szkle lub przezroczystej błonie.

5. Polaroidy.

Polaroidy powstają przez silne rozciągnięcie w jednym kierunku folii plastikowej, która jest zbudowana z długich łańcuchów węglowodorowych; powoduje to ustawienie się cząsteczek szeregami. Następnie zanurza się folię w roztworze zawierającym jod. Jod przyczepia się do łańcuchów węglowodorowych i dostarcza elektronów przewodzących, które mogą się poruszać wzdłuż łańcuchów, ale prostopadle do nich nie. Otrzymuje się w ten sposób jakby „druty” wzdłuż łańcuchów węglowodorowych. Składowa pola elektrycznego wzdłuż drutów zostaje zaabsorbowana, a prostopadła do nich zostaje przepuszczona z bardzo niewielkim wygaszaniem. Płytka polaroidu ma więc oś, zwaną osią łatwego przepuszczania. Jeżeli pole E ma kierunek tej osi, światło przechodzi z bardzo małą absorpcją. Jeżeli E jest prostopadłe do tej osi, światło zostaje prawie całkowicie zaabsorbowane. Oś łatwego przepuszczania jest prostopadła do kierunku rozciągania plastiku, tzn. jest prostopadła do „drutów”.

6. Substancje optycznie czynne.

Światło spolaryzowane liniowo przechodzące przez niektóre kryształy zwane optycznie czynnymi doznaje skręcenia płaszczyzny polaryzacji. Dzieje się to w kryształach jednoosiowych w przypadku, gdy światło biegnie równolegle do osi optycznej. Kierunek skręcenia płaszczyzny polaryzacji jest różny dla różnych kryształów, z których jedne skręcają płaszczyznę polaryzacji w lewo, a inne w prawo. Zgodnie z teorią Fresnela światło spolaryzowane liniowo uważać możemy za nałożenie dwóch spójnych kołowo spolaryzowanych drgań, o równych okresach i amplitudach, lecz przeciwnych zwrotach. W krysztale prędkości obydwu kołowo spolaryzowanych fal stają się różne. W zależności od tego, która fala porusza się szybciej, otrzymamy odpowiednie skręcenie płaszczyzny polaryzacji. Po wyjściu z kryształu obydwa drgania składowe poruszają się już z równą prędkością i płaszczyzna drgań nie zmienia się już więcej. Jest jednak ona skręcona względem płaszczyzny drgań światła wchodzącego do kryształu.

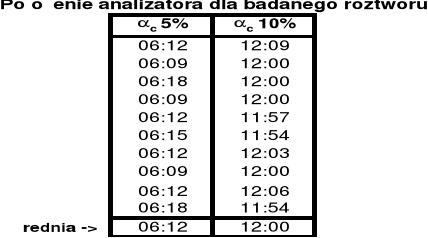
WYNIKI POMIARÓW

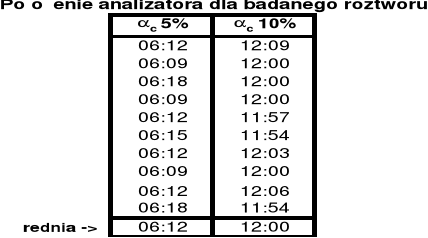
Miara dziesiętna odczytana podczas pomiarów została zamieniona na stopnie.

Format „xx:xx:xx” oznacza odpowiednio „stopnie:minuty:sekundy”

BŁĘDY POMIAROWE WYNIKU ŚREDNIEGO

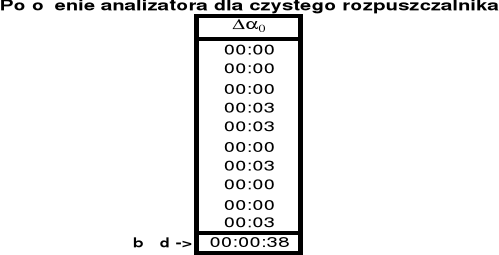
Błąd wartości średniej został wyznaczony ze wzoru:

.

OBLICZENIA

Wzory:

Kąt skręcenia płaszczyzny polaryzacji:

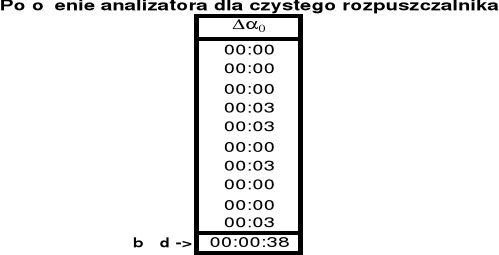
α_o - położenie analizatora dla czystego rozpuszczalnika

α_c - położenie analizatora dla badanego roztworu

c - stężenie roztworu

l - długość rurki pomiarowej

[α] - właściwa zdolność skręcająca

Nachylenie prostej:

Właściwa zdolność skręcająca:

.

Obliczenia:

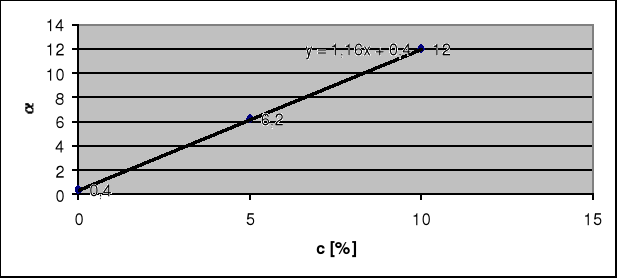
Wykres zależności kąta skręcenia płaszczyzny polaryzacji α od stężenia roztworu c:

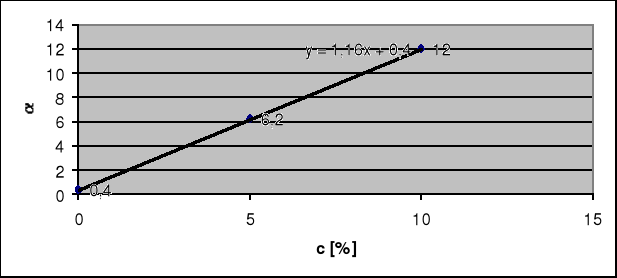
Współczynnik nachylenia prostej został wyliczony przez komputer i wynosi, jak widać zresztą na wykresie a=1,16. Miary kątowe zostały zamienione na miary dziesiętne, a więc:

0°24'=0,4; 6°12'=6,2; 12°00'=12.

Korzystając ze wzoru
na właściwą zdolność skręcającą po podstawieniu wartości otrzymujemy wynik =5,9.

Aby wyliczyć właściwą zdolność skręcającą ze wzoru
, który po przekształceniu daje
, obliczam najpierw kąt skręcenia płaszczyzny polaryzacji α=α_c-α_o.

Średnia wartość α_c=6°12' dla roztworu 5%, oraz α_c=12°00' dla roztworu 10%. α_o=0°24'.

α=6°12'-0°24'=5°48' dla roztworu 5%.

α=12°00'-0°24'=11°36' dla roztworu 10%.

Po podstawieniu wartości [α]=5,9 dla roztworu 5%, oraz taki sam wynik dla roztworu 10%. Jak widać wyniki otrzymane za pomocą obu wzorów są jednakowe.

BŁĘDY POMIAROWE

Błąd współczynnika nachylenia prostej Δa, obliczam ze wzoru:

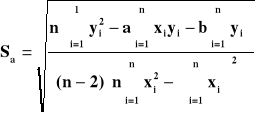
po podstawieniu otrzymałem Δa=8,43*10^-9.

Błędy pomiarowe obliczanych wielkości wyznaczam za pomocą różniczki zupełnej.

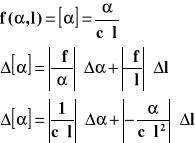
: Δα=0°00'32'' dla 5%; Δα=0°00'55'' dla 10%.

Co po podstawieniu wartości daje:

dla roztworu 5% Δ[α]=0,0090+0,0060=0,0150

dla roztworu 10% Δ[α]=0,0078+0,0060=0,0138

DYSKUSJA BŁĘDÓW

Na błędy powstałe podczas pomiarów wpływ miały następujące czynniki:

• rurka pomiarowa była „nierozbieralna”, przez co nie można było zbyt dokładnie za pomocą linijki określić jej długości (od szkiełka do szkiełka). Trzeba było „na oko” odjąć grubość blachy znajdującej się na szkiełku rurki.

• szkiełka rurki (szczególnie to przy części odkręcanej) były w stanie niemalże uniemożliwiającym obserwację pasków wywoływanych przez przyrząd półcieniowy (były bardzo mocno porysowane).

• w rurce znajdował się podejrzany brud, który mógł wpłynąć na wyniki.

• lampa sodowa dawała dość słabe światło, które miało trudności przedostać się przez słabej jakości rurkę, w której znajdował się roztwór, szczególnie przy wyższym stężeniu.

Odchył od wartości średniej

Odchył od wartości średniej

Odchył od wartości średniej

---