REGULACJA TRÓJPOŁORZENIOEWA
Jednymi z najtańszych i bardzo popularnych elementów, które można wykorzystać jako regulatory przy budowie zamkniętych układów automatyki, są przekaźniki trójpołożeniowe. Istotną ich cechą jest to, że sygnał wyjściowy może mieć tylko trzy różne wartości.
Układy automatyki w których zastosowano przekaźniki trójpołożeniowe jako regulatory nazywamy układami regulacji trójpołożeniowej. Temu typowi regulacji Poświęcony jest niniejszy rozdział.
8,1 Przekaźniki trójpołożeniowe.
Charakterystyka statyczna przekaźnika trójpołożeniowego w przypadku ogólnym jest przedstawiona na rysunku 8,1.
W praktyce znajduje zastosowanie bardzo dużo rozmaitych typów przekaźników trójpołożeniowych. Jako spotykane najczęściej wymienimy przekaźniki elektromechaniczne, elektrotermiczne, hydrauliczne, pneumatyczne, lampowe i magnetyczne bezstykowe. Za klasycznego przedstawiciela przekaźników elektromechanicznych można uważać spolaryzowany przekaźnik elektromagnetyczny którego konstrukcja pokazana jest na rys. 8,2. Wielkością wejściową takiego przekaźnika jest prąd płynący w uzwojeniu między punktami 1-1', wielkością wyjściową zaś - napięcie załączone przez ruchomą kotwiczkę k za pomocą styków 2 lub 2'.
Zasadę działania przekaźnika hydraulicznego przedstawiono na rys. 8,3. Wielkością wejściową jest tu przesunięcie tłoczków w komorze sterującej A, wielkością wyjściową - prędkość poruszania się tłoka w cylindrze B.
Zasadnicza idea konstrukcyjna elektronowych i magnetycznych przekaźników bezstykowych opiera się na pracy elementu wzmacniającego z dodatnim sprzężeniem zwrotnym.
Jeżeli we wzmacniaczu o charakterze elementu inercyjnego pierwszego rzędu o wzmocnieniu ![]()
i stałej czasowej T zastosujemy dodatnie sprzężenie zwrotne za pomocą elementu bezinercyjnego o funkcji przejścia ![]()
(rys.8,4), to funkcja przejścia otrzymanego układu wyrazi się wzorem:
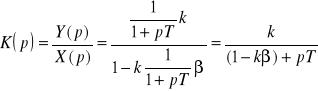
(8.1.)
Dla sygnału wejściowego
![]()
(8.2)
sygnał wyjściowy jest
![]()
, (8.3)
a więc
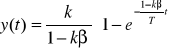
(8.4)
Jeżeli wartości k i β dobraliśmy tak, aby
![]()
(8.5)
to jak wynika ze wzoru (8.4), sygnał y(t)narastałby do nieskończoności, gdyby wzmocnienie wzmacniacza k w całym zakresie pracy układu było stałe.
Praktycznie biorąc charakterystyka wzmacniacza jest zawsze ograniczona nasyceniem. Dlatego wzmocnienie k ze wzrostem sygnałów maleje i narastanie skończy się dla takiej wartości ![]()
dla której ![]()
. Ilustruje to rysunek 8.5. Jeżeli został wzbudzony,
tzn. jego stan określony jest przez punkt A, to dla przejścia od wartości ![]()
ponownie do wartości ![]()
należy do węzła sumacyjnego doprowadzić sygnał ujemny o wartości bezwzględnej większej od ![]()
Wynika stąd przebieg statycznej charakterystyki układu pokazany na rys. 8.6. Jest to charakterystyka przekaźnika dwupołożeniowego za strefą niejednoznaczności ![]()
O wartości strefy niejednoznaczności decyduje wartość funkcji przejścia β zastosowanego sprzężenia zwrotnego.
Przesunięcie charakterystyki (rys.8.6) wzdłuż osi x można uzyskać, wprowadzając do węzła sumacyjnego sygnał pokazujący ![]()
. Charakterystyka statyczna układu ma wówczas kształt pokazany na rys. 8.7.
Dla uzyskania przekaźnika trójpołożeniowego należy zestawić dwa układy omawiane poprzednio w sposób pokazany na rys.8.8.
Jako przykład praktycznego wykorzystania przekaźnika bezstykowego pokazany jest na rys. 8.9 schemat bezstykowego przekaźnika magnetycznego. Do jego konstrukcji wykorzystano dwa wzmacniacze magnetyczne o układzie szeregowym, w których dla uzyskania działania przekaźnikowego zastosowano dodatnie sprzężenie zwrotne prądowe.
8.2. Funkcja opisująca przekaźniki trójpołożeniowe.
Przekaźnik trójpołożeniowy jest jak wynika z bezpośrednio z jego charakterystyki, elementem nieliniowym. Dla zanalizowania pracy układu automatyki, w którym przekaźnik zostanie zastosowany, trzeba będzie więc korzystać z którejś z metod analizy układów nieliniowych, np. metody pierwszej harmonicznej lub metody płaszczyzny fazowej. Stosując metodę pierwszej harmonicznej należy znać tak zwaną funkcję opisującą dany element nieliniowy, określona wzorem (7.14). Obliczymy tę funkcję dla przekaźnika trójpołożeniowego bez strefy niejednoznaczności, tylko ze strefą nieczułości a. Charakterystyka statyczna takiego przekaźnika przedstawiona jest na rys. 8.10.
Aby obliczyć funkcję opisującą ten przekaźnik, rozpatrzymy przebieg sygnału wyjściowego y, wywołany wprowadzeniem na wejście sygnału sinusoidalnego ![]()
.
Przebieg ten jest pokazany na rysunku 8.11. Ponieważ przyjęliśmy jednoznaczną charakterystykę przekaźnika, więc na podstawie wzoru (7.16) jest ![]()
. Dla obliczenia funkcji opisującej należy znaleźć tylko współczynnik ![]()
według wzoru (7.15):
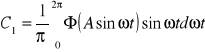
Na podstawie rysunku 8.11jest:
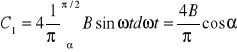
(8.6)
Ponieważ ![]()
, więc
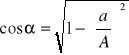
(8.7)
Ostatecznie jest
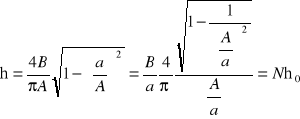
(8.8)
gdzie:
![]()
(8.9)
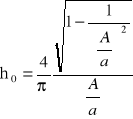
(8.10)
N jest tzw. normą przekaźnika zależną od jego danych: strefy nieczułości a i wartości B sygnału wyjściowego. ![]()
jest tzw. znormowaną funkcją opisującą przekaźnik, wspólną dla wszystkich elementów o charakterystyce pokazanej na rys. 8.11.
Zależność unormowanej funkcji opisującej ![]()
od wartości A/a pokazano na rys. 8.12.
Maksimum tej funkcji jest dla wartości A/a=![]()
i wynosi ![]()
Na rysunku 8.13 pokazano zależność odwrotności znormalizowanej funkcji opisującej przekaźnik od wartości A/a. Minimum tej funkcji jest dla wartości A/a=![]()
i wynosi ![]()
. Przebieg funkcji -1/![]()
na płaszczyźnie ![]()
pokazany jest na rys. 8.14.
8.3. Analiza pracy układów regulacji przekaźnikowej metodą pierwszej harmonicznej.
Schemat blokowy prostego układu regulacji trójpołożeniowej przedstawiony jest na rys. 8.15. Składa się on z części liniowej o funkcji przejścia K(p) i przekaźnika o funkcji opisującej ![]()
. Warunek wzbudzenia takiego układu można w przybliżeniu określić według wzoru:
![]()
,
w którym ![]()
jest charakterystyką częstotliwościową części liniowej układu, ![]()
zaś funkcją opisującą elementu nieliniowego.
W przypadku przekaźnika jest według wzoru (8.8)
![]()
.
Warunek powstania oscylacji można więc napisać w postaci
![]()
(8.11)
lub
![]()
Przebieg ![]()
na płaszczyźnie ![]()
pokazano na rys. 8.16.
Symbol ![]()
oznacza częstotliwość, dla której przesunięcie fazowe miedzy sygnałem wprowadzonym na wejście części liniowej układu a sygnałem otrzymanym na wyjściu wynosi ![]()
. Symbol ![]()
oznacza wzmocnienie dla tej częstotliwości.
Z rysunku 8.16 widać, że warunkiem absolutnej stabilności układu z przekaźnikiem trójpołożeniowym jest
![]()
,
czyli
![]()
. (8.12)
Jeżeli
![]()
. (8.13)
a więc krzywa ![]()
jest styczna do krzywej ![]()
, to odpowiada to stanowi układ na granicy stabilności. Jeżeli natomiast
![]()
. (8.14)
(co na rys. 8.16 oznaczono linią przerywaną), to dla zaburzeń z<A2 układ będzie stabilny, zaś dla zaburzeń z>A2 nastąpi wzbudzenie z amplitudą A1 i częstotliwością ![]()
. W układach nieliniowych jest to jednak, w porównaniu z układami liniowymi, pojęcie bardzo subtelne i lepsze zrozumienie tego zjawiska może dać metoda płaszczyzny fazowej, omawiana w następnym paragrafie.
Z rysunku 8.16 wynikają wprost trzy najprostsze sposoby ustabilizowania takiego układu w przypadku wzbudzenia :
zmniejszenie wzmocnienia części liniowej,
zmniejszenie wartości sygnału B załączonego przez przekaźnik,
zwiększenie strefy nieczułości a przekaźnika,
Są to jednak sposoby najprostsze, pociągające za sobą pogorszenie własności dynamicznych układu.
Metody stabilizacji, nie powodujące niekorzystnych zmian własności dynamicznych układu, polegają na zastosowaniu dodatkowych sprzężeń zwrotnych. Wygodnie jest przedstawić korzystając z metody płaszczyzny fazowej i dlatego zostaną omówione w paragrafie poświęconym tej metodzie.
Przykład. Proponujemy obliczyć warunek stabilności układu regulacji automatycznej, składającego się z obiektu astatycznego o funkcji przejścia ![]()
i przekaźnika trójpołożeniowego o strefie nieczułości a i bez strefy niejednoznaczności. Należy uwzględnić, że przekaźnik działa z opóźnieniem T.
Czas opóźnienia T w działaniu przekaźnika można uwzględnić przez wprowadzenie do schematu analizowanego układu członu o funkcji przejścia ![]()
, jak to przedstawiono na rys. 8.17. Układ można więc podzielić na część liniową o funkcji przejścia
![]()
i część nieliniową o funkcji opisującej
![]()
gdzie B i a - parametry przekaźnika, ![]()
- unormowana funkcja opisująca.
Wzajemne usytuowanie charakterystyki części liniowej i funkcji opisującej na płaszczyźnie ![]()
pokazano na rys. 8.18.
Oznaczymy symbolem ![]()
częstotliwość, dla której po raz pierwszy następuje przecięcie charakterystyki częstotliwościowej części liniowej z osią rzeczywistych. Częstotliwość tę możemy obliczyć z warunku
![]()
Ponieważ
![]()
więc
![]()
,
a stąd
![]()
.
Część rzeczywista funkcji przejścia dla częstotliwości ![]()
jest
![]()
.
Warunkiem stabilności jest więc
![]()
,
a stąd
![]()
.
8.4. Analiza pracy układów regulacji trójpołożeniowej
metodą płaszczyzny fazowej.
Niech będzie dany układ regulacji trójpołożeniowej przedstawiony na rys. 8.19. Składa się on z obiektu astatycznego z inercją o funkcji przejścia ![]()
oraz z przekaźnika o charakterystyce
![]()
(8.15)
Równanie obiektu jak wynika z funkcji przejścia, jest
![]()
(8.16)
a równanie węzła sumacyjnego
![]()
(8.17)
Zakładając, że sygnał sterujący s ma wartość stałą, otrzymamy na podstawie wzorów (8.15), (8.16), (8.17)
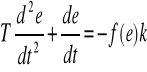
(8.18)
Przeprowadzimy obecnie analizę przebiegów regulacyjnych w omówionym układzie z rys. 8.19 dla różnych typów przekaźników .
Przekaźnik bez strefy nieczułości i bez strefy niejednoznaczności.
Charakterystyka przekaźnika bez strefy nieczułości i bez strefy niejednoznaczności przedstawiona jest na rys. 8.20a. Jak wynika bezpośrednio z tego rysunku w tym przypadku jest
![]()
(8.1)
równanie (8.18) ma więc postać
![]()
(8.19)
Prawa strona równania (8.20) jest funkcją nieciągłą o jednym punkcie nieciągłości, e=0. Prosta o równaniu e=0, czyli oś e będzie w tym przypadku tak zwaną prostą przełączeń lub komutacji. Prosta ta dzieli płaszczyznę fazową na dwie półpłaszczyzny:
lewą e<0 i prawą e>0. W każdym z tych obszarów przebiegi regulacyjne określone będą równaniem
![]()
(8.21)
przy czym znak + odnosi się do lewej strony, a znak - do prawej półpłaszczyzny.
Dla obliczenia trajektorii fazowych przedstawiamy równanie (8.21) w postaci
![]()
, (8.22)
skąd po scałkowaniu
![]()
, (8.23)
gdzie C - stała określona warunkami początkowymi.
Trajektorie fazowe, narysowane na podstawie równania (8.23) przedstawione są na rys. 8.20b.
Przekaźnik ze strefą nieczułości
Charakterystyka przekaźnika ze strefą nieczułości, ale bez strefy niejednoznaczności, przedstawiona jest na rys. 8.21a. W tym przypadku charakterystykę przekaźnika określają równania:
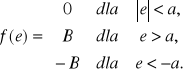
Prawa strona równania (8.18) jest w tym przypadku funkcją o dwóch punktach nieciągłości ![]()
i ![]()
. Prostymi komutacji będą więc dwie proste o równaniach ![]()
i ![]()
, czyli proste równoległe do osi ![]()
i oddalone od niej o odcinek a ,jedna na lewej, druga zaś na prawej półpłaszczyźnie. Podzielą one płaszczyznę na trzy obszary: I, II, III, jak zaznaczono na rys. 8.21.b.
W obszarach I i III trajektorie fazowe opisane są identycznym jak w poprzednim przypadku wzorem (8.21). W obszarze II jest natomiast
![]()
,
a stąd
![]()
(8.24)
gdzie ![]()
i ![]()
oznaczają warunki początkowe.
Trajektorie fazowe narysowane na podstawie wzorów (8.24) i (8.21) przedstawiona są na rysunku 8.21b.
Przekaźnik ze strefą niejednoznaczności
Charakterystyka przekaźnika ze strefą niejednoznaczności, ale bez nieczułości przedstawiona jest na rysunku 8.22a. W tym przypadku charakterystykę przekaźnika określają równania:
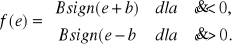
Liniami przełączeń będą więc w tym przypadku dwie półproste: e = b w górnej i e = -b w dolnej półpłaszczyźnie, jak pokazano na rys. 8.22b. Podzielą one płaszczyznę fazową na dwa obszary, w których trajektorie fazowe określone będą wzorem (8.23). Przebieg ich będzie taki jak pokazano na rys. 8.22b.
Przekaźnik ze strefą niejednoznaczności i strefą nieczułości.
Charakterystyka przekaźnika ze strefą niejednoznaczności i strefą nieczułości przedstawiona jest na rys. 8.23a. W tym przypadku, jak bezpośrednio wynika z charakterystyki przekaźnika, liniami komutacji są:
w I ćwiartce półprosta e = a+b,
w II ćwiartce półprosta e = a,
w III ćwiartce półprosta e = -a-b,
w IV ćwiartce półprosta e = -a
W poszczególnych obszarach , na jakie tymi prostymi została podzielona płaszczyzna fazowa, trajektorie fazowe są określone odpowiednio wzorami (8.23) i (8.24), Ich przebiegi są przedstawione na rys. 8.23b.
---------------- ----------------------- --------
Przeanalizujemy jeszcze wpływ czasu opóźnienia T0 w działaniu przekaźnika na przebieg procesu regulacji w badanym układzie. Załóżmy, że charakterystyka przekaźnika ma strefę nieczułości, ale nie ma strefy niejednoznaczności, jak pokazano na rys. 8.24a.
Czas opóźnienia przekaźnika T0 można uwzględnić przez wprowadzenie do schematu analizowanego układu członu o funkcji przejścia ![]()
, jak przedstawiona na rys. 8.24. Uwzględniając oznaczenia na rys. 8.24, możemy napisać, że:
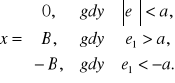
------------- ---------------- --------------------------------
W przypadku gdy ![]()
, można przyjąć, że po zaburzeniu jednostkowym sygnał e zmienia się liniowo, wtedy
![]()
,
czyli
![]()
.
Liniami przełączeń będą proste
![]()
Trajektoria fazowa układu z opóźnieniem przedstawiona jest na rys. 8.25. Widać z niej wyraźnie niekorzystny wpływ czasu opóźnienia na stabilność.
Dla poprawy własności dynamicznych układów regulacji przekaźnikowej wprowadza się często na wejście przekaźnika pochodną sygnału błędu, jak to przedstawiono na schemacie (rys. 8.26). Funkcja f(e) będzie w tym przypadku miała postać
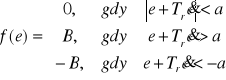
------------------- --------------------- --------------------------
a stąd równanie prostych przełączeń
![]()
.
Trajektoria fazowa układu z wprowadzoną z wprowadzoną pochodną przedstawiona jest na rys. 8.27.Widać z niej dobrze, że wprowadzenie pochodnej poprawia warunki stabilności układu. Często dla zmniejszenia przeregulowań lub stabilizacji układu stosuje się dodatkowe sztywne sprzężenia zwrotne z wyjścia serwomotoru (rys. 8.28). W tym przypadku
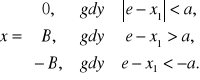
Na podstawie rys. 8.28 znajdujemy
![]()
,
![]()
,
skąd
![]()
lub w postaci czasowej
![]()
.
-------------- ------------ ------------
Równania prostych przełączeń będą
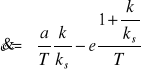
. (8.26)
Proste te przecinają oś e w punktach
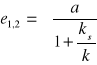
. (8.27)
Sztywne sprzężenie zwrotne zmniejsza więc również strefę nieczułości. Wskutek pochylenia prostych przełączeń w lewo ulegają zmniejszeniu przeregulowania (rys. 8.29).
8.5. Analiza pracy układów regulacji trójpołożeniowej
w przestrzeniach metrycznych .
Niech będzie dany układ regulacji trójpołożeniowej przedstawiony na rys. 8.30. Składa się on z elementu całkującego z inercja o funkcji przejścia
![]()
i przekaźnika o charakterystyce
![]()
(8.28)
Równanie części liniowej układu jest więc
![]()
, (8.29)
----------- ----------------------------
Równanie węzła sumacyjnego
![]()
. (8.30)
Zakładając s=const otrzymamy
![]()
lub oznaczając
![]()
, ![]()
,
![]()
. (8.31)
Przekaźnik bez histerezy
Przyjmujemy jako miarę odległości punktu o współrzędnych ![]()
od początku układu wyrażenie
![]()
![]()
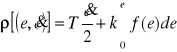
. (8.32)
Tak określona funkcja ![]()
będzie funkcją dodatnią i będzie spełniać aksjomaty metryki, jeżeli charakterystyka przekaźnika f(e) będzie bez histerezy i będzie położona w ćwiartce pierwszej i trzeciej płaszczyzny [f(e),e] tak jak to pokazano na rys. 8.31.
Zastępując ![]()
przez ![]()
i całkując obie strony równania (8.31) otrzymamy
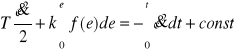
, (8.33)
stąd
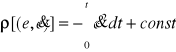
, (8.34)
oraz
![]()
Wynika stąd, że jedynym warunkiem stabilności układu z rys. 8.30 jest, aby charakterystyka przekaźnika była jednoznaczna (bez histerezy) i była położona w pierwszej i trzeciej
------------ --------
ćwiartce płaszczyzny [f(e),e] (rys.8.32). Wtedy bowiem wyrażenie określone wzorem (8.32) spełnia warunki odległości, a pochodna tej odległości wzdłuż trajektorii równania (8.31) jest ujemna i równa zeru tylko dla ![]()
.
Tak więc układ regulacji przekaźnikowej z rys. 8.30 jest stabilny dla dowolnych wartości wzmocnienia k i stałej czasowej T, jeżeli tylko przekaźnik jest bez histerezy.
Przekaźnik z histerezą
Charakterystyka przekaźnika z histerezą, na przykład przedstawiona na rys. 8.33, nie jest jednoznaczna. W takim przypadku całka
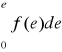
może być ujemna, mimo że charakterystyka f(e) będzie położona w pierwszej lub trzeciej ćwiartce, tak jak to pokazuje rys.8.34
W tym przypadku, mimo że wartości k i T będą dodatnie, a charakterystyka f(e) będzie położona w pierwszej i trzeciej ćwiartce, wyrażenie
![]()
![]()
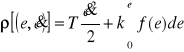
.
może być ujemne.
To tłumaczy znane zjawisko, że układ przedstawiony na rys. 8.30 jest stale stabilny, jeżeli przekaźnik jest bez histerezy, a może być niestabilny, jeżeli przekaźnik posiada histerezę.
Zbadajmy teraz stabilność układu z rys. 8.30, przyjmując jako miarę odległości punktu ![]()
od początku układu współrzędnych
![]()
![]()
![]()
. (8.35)
Będzie ona spełniać warunki dodatniości , gdy T>0, co zachodzi.
------------ ----------------------- -------------------
Obliczamy pochodną tej odległości wzdłuż trajektorii równania (8.31). Otrzymamy
![]()
![]()
(8.36)
Wykorzystując równanie (8.31) i eliminując ![]()
otrzymujemy
![]()
Aby pochodna była ujemna wystarczy, aby były spełnione następujące nierówności:
![]()
, ![]()
. (8.37)
Jeżeli te warunki są spełnione, to układ jest stabilny bez względu na to, czy przekaźnik posiada histerezę, czy nie.
Stabilizacja przez wprowadzenie pochodnej.
Załóżmy, że przekaźnik w schemacie na rys.8.30 posiada histerezę i spróbujmy zapewnić stabilność tego układu przez wprowadzenie pochodnej sygnału błędu (odpowiedni schemat połączeń przedstawiony jest na rys. 8.35).
Działanie tego układu opisane jest następującymi równaniami:
obiekt ![]()
, (8.38)
serwomotor ![]()
, (8.39)
przekaźnik ![]()
, (8.40)
układ korekcyjny ![]()
, (8.41)
węzeł sumacyjny ![]()
, (8.42)
które prowadzą do jednego równania różniczkowego nieliniowego
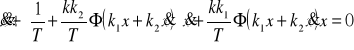
. (8.43)
Dla uproszczenia zapisu oznaczymy
![]()
, ![]()
, ![]()
, (8.44)
![]()
.
---------- ----------------------------------------
Otrzymamy równanie typu
![]()
. (8.45)
Zbadajmy stabilność tego równania przyjmując następującą miarę odległości :
![]()
![]()
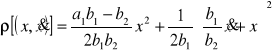
. (8.46)
Będzie ona dodatnia, jeżeli
![]()
![]()
![]()
, ![]()
,
![]()
![]()
![]()
, ![]()
(8.47)
Obliczmy obecnie pochodną tej odległości wzdłuż trajektorii równania (8.45). Otrzymamy
![]()
![]()
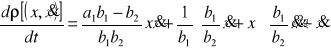
. (8.48)
Po elementarnych przekształceniach równania (8.45) otrzymamy
![]()
![]()
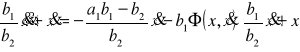
. (8.49)
Stąd, wprowadzając do drugiego wyrazy (8.48) otrzymamy
![]()
![]()
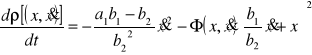
.
Pochodna odległości![]()
będzie ujemna jeżeli
![]()
,
![]()
, (8.50)
Porównanie wzorów (8.50) i (8.47) prowadzi do następujących warunków stabilności
![]()
, ![]()
, ![]()
, ![]()
,
![]()
,
lub, przechodząc na współczynniki wzmocnienia i stałe czasowe,
![]()
, ![]()
, ![]()
,
oraz
![]()
, ![]()
,
![]()
,
Jeżeli te warunki są spełnione, to układ pozostaje stabilny bez względu na to czy przekaźnik posiada histerezę, czy nie.
Wyszukiwarka