Opis Wyspy

Platon przedstawia Atlantydę, jako dużą wyspę, ale w dialogu "Kritias" w miarę szczegółowo omawia tylko rozciągającą się na niej równinę. Tylko jeden jej bok, ten łączący ją bezpośrednio z morzem, był chyba w miarę płaski, jakkolwiek można mieć co do tego wątpliwości, bo w pewnym miejscu Kritias Młodszy (w dialogu "Kritias") powiada:

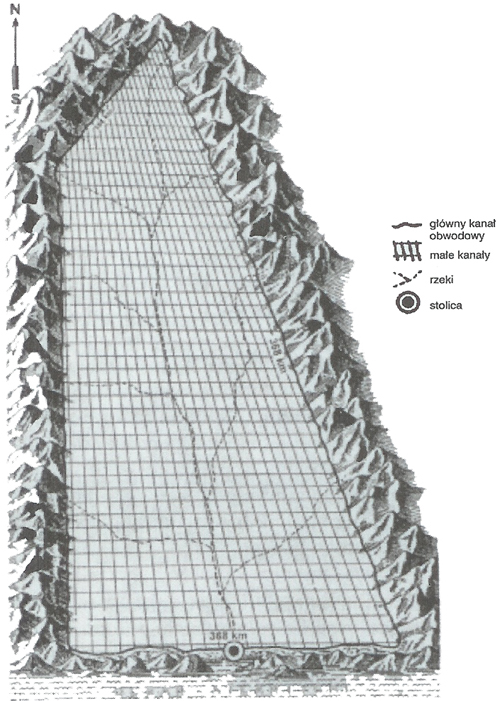
« Plan żyznej równiny z siecią kanałów i stolicą imperium Atlantydy według Żyrowa.

"Więc naprzód miała być ta cała okolica bardzo wysoka i odcięta od morza a naokoło miasta nic, tylko równina, miasto otaczająca a sama dookoła otoczona górami, które schodziły aż do morza, gładka i równa i bardzo długa".

Z treści całego opisu wynika jednak, że owo "odcięcie od morza" nie stanowiło bariery niemożliwej do pokonania. Znacznie wcześniej bowiem mówi:

"Od brzegu morza aż do środka całej wyspy była równina. Najpiękniejsza miała być ze wszystkich równin i zadowalającej była wartości".

Z kolei zdanie:

"Ona była czworoboczna po większej części, prosta i długa" informuje o kształcie tej równiny. Do pełnego jej opisu brakuje jeszcze konkretnych wymiarów. Z tym trochę gorzej, bo o wymiarach równiny informują dwie wzmianki. A więc:

"Ciągnęła się po drugiej stronie miasta na trzy tysiące stadiów, a na środku od morza w górę na dwa tysiące".

Ponieważ uważa się, że stadion odpowiada 185 m. przeto te wartości odpowiadają 555 km i 370 km .

O wymiarach równiny świadczy także druga wzmianka:

"A czego nie dokonywało, to wyprostowywał rów naokoło niej wykopany, jego głębokość, szerokość i długość podają niewiarygodną. Trudno uwierzyć, żeby w porównaniu do innych robót tak wielkie dzieło było rękami ludzkimi wykonane, ale trzeba powiedzieć cośmy przecież słyszeli. Głęboki był na jeden plethron, a szeroki był wszędzie na jeden stadion, a że go wykopano naokoło całej doliny, więc jego długość wypadła na dziesięć tysięcy stadiów".

Jedno plethron odpowiada odległości 30 m, a więc rów miał głębokość 30 m, szerokość 185 m, a całkowita jego długość wynosiła 1850 km. Wymiary imponujące nawet na współczesne czasy (!) i chyba dlatego ustami Kritiasa Platon zastrzegał się,, że "...jego głębokość, szerokość i długość podają niewiarygodną". Skoro zaś kanał był wykopany na obrzeżach, przeto można przyjąć, że obwód tej czworokątnej równiny wynosił właśnie 1850 km. Owe trzy tysiące stadiów, czyli 555 km " po drugiej stronie miasta", można chyba uznać za jeden z jej czterech boków. Na pozostałe trzy boki zostaje więc 1295 km. Jak potraktować ten drugi wymiar, tzn. "a na środku od morza w górę na dwa tysiące" (stadiów)? Wydaje się, że nieco rozjaśnia tę sprawę następne zdanie:

"Całą okolica wyspy była zwrócona ku południu a od północy osłonięta od wiatrów".

Można na tej podstawie przyjąć, że równina ku południu łagodnie się obniżała, a południowy jej brzeg przebiegał wzdłuż wybrzeża i gdzieś mniej więcej od środka tego boku odległość do naprzeciwległego, górnego boku wynosiła owe dwa tysiące stadiów, czyli 370 km. Niestety, niewiele można z tego wywnioskować o długościach pozostałych trzech boków.

Omawiając zagadnienie wymiarów równiny, Żyrow przytacza przytacza dane pochodzące od Rousseau-Liessensa, że czworoboczna równina miała następujące wymiary: bok zachodni 552 km, wschodni736 km, południowy (wybrzeże) - 368 km, a na północy długie boki łączył bok czwarty, najkrótszy, o długości 184 km. Jeśliby tak istotnie było, to owa równina byłaby wydłużona w kierunku północ południe, z czym można się zgodzić z uwagi na cytowane uprzednio zdanie, iż "Cała okolica wyspy była zwrócona ku południowi a od północy osłonięta od wiatrów". Można także zgodzić się z tym, że jeden jej bok miał długość około 552 km (trzy tysiące stadiów) i że najprawdopodobniej przebiegał w kierunku mniej więcej południkowym.

Ławo zauważyć, że owe dwa tysiące stadiów "na środku od morza w górę", czyli 370 km, Rousseau-Liessens przyjął za długość boku południowego, będącego jednocześnie linią wybrzeża. W takim razie pozostało jeszcze na dwa boki 925 km. Przyjął więc, że bok wschodni miał 736 km, a najkrótszy, północny - 184 km. Żyrow wyjaśnia, że ów atlantolog (czy też atlantoman) przyjął, iż długości czterech boków mają się do siebie jak 1:2:3:4 i że - być może była to uznawana przez Platona mistyka liczb. Stawia to pod znakiem zapytania wiarygodność takich właśnie wymiarów ale nie są one całkiem nie do przyjęcia. Można się bowiem zgodzić, że czworokątna równina nie była równoległobokiem. W każdym razie, wystarczy długość jednego boku, wynosząca 555 km, żeby zgodzić się, iż istotnie była bardzo długa. Według wymiarów przytoczonych przez Żyrowa, obwód czworobocznej równiny wynosiłby 1840 km. Oczywiście, różnica 10 km byłaby tu bez znaczenia. Z takimi wymiarami zgodził się w swej książce Andrzej Marks.

O bezwzględnej wielkości równiny daje wyobrażenie także jej powierzchnia. Według wymiarów przyjętych przez Rousseau-Liessensa miałaby około 170 000 km kw. Natomiast założywszy, że miała kształt zbliżony do kwadratu, to przy obwodzie 1850 km jeden bok miałby długość 1850:4=462,5 km. Powierzchnia kwadratu o takim boku wynosiłaby więc 213 906 km kw., czyli ok. 214 km kw. Wreszcie z faktu, że "wielkość takiego działu wynosiła nieraz dziesięć razy dziesięć stadiów a wszystkich działów było sześćdziesiąt tysięcy" można się doliczyć, że całkowita powierzchnia mogłaby wynosić około 205 000 km kw .

O czym mówią te wartości?

Powierzchnię wyliczoną przy założeniu jej kwadratowego kształtu przy danym obwodzie (1850 km) należy uznać za maksymalną. Większa niż 214 000 km kw. być nie mogła. Z kolei zwrot Platona "wielkość takiego działu wynosiła nieraz dziesięć razy dziesięć stadiów" niewątpliwie świadczy o tym, że miały one kształt zbliżony do kwadratu i że "działy" o takich wymiarach były największe. Skoro były i mniejsze, to owa maksymalna powierzchnia byłaby bliższa wartości około 205 00 km kw. W takim Razie powierzchnia wynikająca z wymiarów wydedukowanych przez Rousseau-Liessensa, czyli około 170 000 km kw., wygląda dość prawdopodobnie.

Równinę, tzn. na pewno boki : zachodni, północny i wschodni, otaczały góry, "które schodziły aż do morza" ale o nich w wystąpieniu Kritiasa brak danych. Nie wiadomo, jaka była ich wysokość i szerokość. Z wymiarów równiny można jedynie wnosić, że była to dość duża wyspa, ale dobrze byłoby wiedzieć, jaki procent jej powierzchni zajmowała ta właśnie równina. Jest to o tyle frapujące, że Kritias powiada, iż "Od brzegu morza aż do środka całej wyspy była równina".

Zwrot "do środka" można rozumieć jako "do wnętrza", ale może to oznaczać "do centrum", czy też " do połowy wyspy". Wtedy cała wyspa miałaby rozmiary co najmniej dwukrotnie większe niż opisywana równina.

Nie mniej intrygujące jest następne zdanie: "Najpiękniejsza miała być ze wszystkich równin i zadowalającej była wartości". Jak rozumieć wyrażenie " najpiękniejsza ... ze wszystkich równin"? Czy najpiękniejsza ze wszystkich równin w całym znanym wówczas świecie, czy też najpiękniejsza ze wszystkich równin na wyspie Atlantydzie? Ta druga ewentualność oznaczałaby, że oprócz opisywanej równiny były jeszcze inne. Ile ich mogło być? Zwrot "ze wszystkich równin" pozwala przypuszczać, że chyba więcej niż tylko jeszcze jedna. Jakie były wymiary pozostałych?

Z tych dwóch zdań wypowiedzi Kritiasa można więc wyciągnąć wnioski niejako "powiększające" powierzchnię Atlantydy do być może nawet imponujących rozmiarów, większych niż podane wcześniej porównanie, że miała być "większa od Libii i Azji razem wziętych".

---