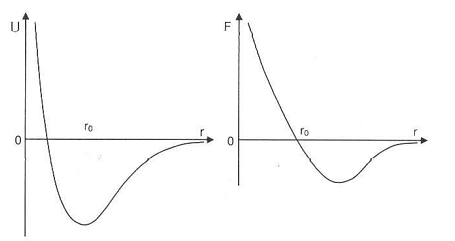
1. Atomy oddziaływają między sobą siłami zależnymi od odległości między nimi. Przy pewnym ro en. potencjalna jest minimalna, a siła = 0. Wtedy atomy są w równowadze. Gdy odległość między atomami ulegnie zmianie (np. w skutek F zewn.) pojawi się siła sprężystości działająca w takim kierunku by przywrócić stan równowagi (gdy r > ro atomy się przyciągają - siła ujemna i odwrotnie).

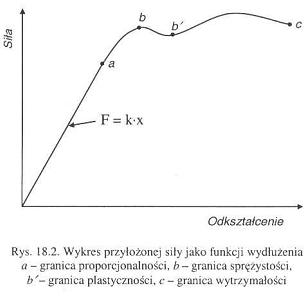
2. Gdy zmieniają się odległości między atomami np. na wskutek działania F zewn, następuje jakaś deformacja ciała - odkształcenie. Gdy siła znika i ciało powraca do poprzedniego kształtu, jest to odkształcenie sprężyste, natomiast gdy odkształcenie nie znika całkowicie, jest nazywane plastycznym.

Granica proporcjonalności - granica do której stosuje się prawo Hooke'a, czyli że siła jest proporcjonalna do odkształcenia.

Granica sprężystości - granica od której powstają odkształcenia plastyczne.

Granica wytrzymałości - ulega zerwaniu.

3. Naprężenie normalne - stosunek siły normalnej (prostopadłej) do powierzchni. Naprężenie styczne - gdy siła jest styczna do powierzchni.

Odkształcenie względne - przyrost długości Δl do długości początkowej l pod wpływem naprężeń normalnych.

4. Prawo Hooke'a - wydłużenie względne jest wprost proporcjonalne do naprężenia normalnego.

Moduł Younga - liczbowo to wartość naprężenia jakie jest potrzebne do wydłużenia ciała o wartość początkową.

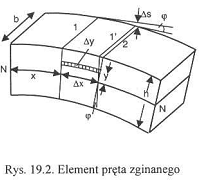
Prawo Hooke'a w stosunku do ugięcia - gdy na podłużny pręt działa siła prostopadła do jego długości, ulega on ugięciu, a wartość tzw. strzałki ugięcia jest proporcjonalna do siły F, a także zależy od wymiarów geometrycznych pręta, sposobu jego mocowania oraz rodzaju materiału z którego jest wykonany.

5. Strzałka ugięcia - z prawa Hooke'a: gdzie z S=bΔy, l=Δx, Δl=yφ

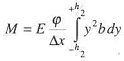
Moment siły wzgl. warstwy N: Dla wszystkich warstw między przekrojami 1 i 2:

Gdy : to:

Moment siły wzgl. przekroju 2 wynosi M=F(l-(x+Δx))=F(l-x); Ponadto:

Po połączeniu: elementarna strzałka ugięcia: Całkowita strz. ug:

Strzałki ugięcia dla obu przekrojów:

- prawo Hooke'a w stosunku do ugięcia

Dla pręta podpartego z dwóch stron i obciążonego na środku:

6. Moduł Younga można obliczyć np. metodą regresji liniowej ze wzorów na strzałki ugięcia, ponieważ ta wartość jest liniowo zależna od siły. Współczynnik a jest równy:

7. Regresja liniowa: gdy mamy zależność liniową y=ax+b, mierzymy x i y i możemy obliczyć współczynniki regresji a i b.

---