Wykład 13.

Przybliżenie adiabatyczne ( Borna -Oppenhaimera)

Do tej pory zajmowaliśmy się opisem elektronów poruszających się w polu nieruchomych jonów. Oczywiście wiemy , że w realnych układach ( drobinach lub kryształach jądra atomów nie są nieruchome ( nawet w temperaturze 0K jądra wykonują pewne drgania o energii
(
jest stałą Plancka a
częstością kołową drgań) . Uwzględnienie ruchu jonów lub jąder będzie tematem tego wykładu.

Możemy skorzystać z wniosków poprzedniego wykłady i przyjąć, że udało nam się obliczyć energie i funkcje własne układu wielolelektronoiwego w przybliżeniu jenoelektronowym dla danych położeń jonów.

Możemy więc rozważać każdy elektron osobno używające do jego opisu hamiltonianu
i funkcji falowej
.

Jeśli elektron znajduje się w krysztale lub drobinie składającej się z N jąder całkowita energia układu będzie opisana hamiltonianem

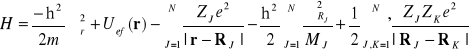
(II-1)

W hamiltonianie tym pierwsze trzy człony są znanym nam już hamiltonianem jednoelektronowym z efektywnym potencjałem opisującym oddziaływania międzyelektrodowe, w którym potencjał oddziaływania elektron z jądrami przedstawiono jako sumę potencjałów poszczególnych jąder. Czwarta suma reprezentuje energię kinetyczną jąder zaś piąta suma energię potencjalna odpychania ładunków jąder. Literami Z_J i M_J z indeksami oznaczono odpowiednio liczby atomowe i masy jąder. Literą R_J oznaczono położenia jąder.

Na ogół drgania sieci krystalicznej lub drobin nie polegają na niezależnych drganiach wszystkich jonów. Zawsze mamy do czynienia z ruchem uporządkowanym, w którym jądra drgają mnie lub bardziej symetrycznie. Współrzędne opisujące ruch jąder są od siebie wzajemnie zależne. Nie ma więc potrzeby używania N niezależnych położeń W najprostszym przypadku ruch wszystkich jąder będzie mógł być opisany jedna współrzędną R

Przybliżenie adiabatyczne

Jako interesujący przykład można rozpatrzyć cząsteczkę dwuatomową , np. H_2, lub jon metalu w związku koordynacyjnym np. CrO₆ .

a

H

R=|R₂-R₁|

R₂

H

R₁

b

R

Rysunek 1 a i b

W oby przypadkach drania układu jonów można opisać przy pomocy jednej współrzędnej, R . Powoduje to ,że hamiltonian może być przedstawiony w znacznie prostszej postaci

(II-2)

gdzie H_e i H_j są operatorami opisującymi ruch elektronów i jąder

(II-3)

Skoro dokonano separacji zmiennych można przedstawić funkcje falową w postaci iloczynu :

(II-4)

Funkcja w tej postaci nosi czasem nazwę funkcji Borna Oppenhaimera . Pierwszy składnik jest funkcją elektronową , opisującą ruch elektronów dla danych położeń jąder . Obrazuje to równanie Shrödingera w postaci

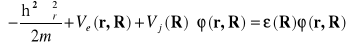
(II-5)

gdzie
jest parametrycznie zależną od położeń jąder energią elektronów. Należy zwrócić uwagę, że w równaniu (II-5) występuje potencjał oddziaływania jąder. Dla elektronu jest stała , zależna od położeń jąder . Na ogół stałe elementy hamiltonianu są pomijane . W tym przypadku bierzemy to je pod uwagę. Robimy to ponieważ w całkowitym hamiltonianie układu (II-2) jest to funkcja zależna od położeń jąder.

Zobaczmy teraz , w jakim przypadku możemy interpretować równanie (II-5) jako równanie Shrödingera dla elektronów. W ogólnym przypadku możemy rozwiązywać równanie z hamiltonianem (II-2) i funkcją (II-4) . Otrzymamy :

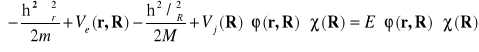
(II-6)

W równaniu tym energia E jest energia własną układu elektronów i jonów . Można przyjąć następujący warunek normalizacji funkcji falowych :

(II-7)

Równanie (II-6) da się przepisać w postaci:

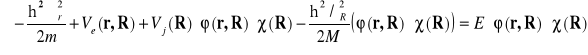
(II-8)

Drugi składnik równania daje się zapisać w postaci :

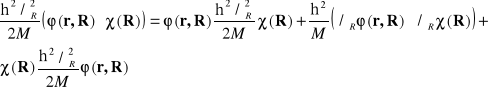
(II-9)

Pierwszy składnik w równaniu (II-9) reprezentuje energię kinetyczną jonów (czynnik
) pomnożoną przez elektronowa funkcję falową, dwa pozostałe stanowią tzw. Operator nieadiabatyczności . Formalnie dokonujemy przybliżenia adiabatycznego gdy zakładamy, że :

(II-10)

Przybliżenie to jest uzasadnione we wszystkich przypadkach , gdy elektronowa funkcja falowa , nie zależy lub bardzo słabo zależy od położeń jąder. Na ogół przypadku wielu molekuł założenie to jest spełnione. W przypadku kryształów mamy do czynienia z bardziej skomplikowaną sytuacją i założenie o adiabatyczności układu trzeba zawsze osobno analizować. Często pomija się operator nieadiabatyczności argumentując , że w wyniku jego działania dostajemy poprawki do wartości energii rzędu
( stosunku masy elektronu do masy jonu).

Jeśli założy się spełnienie warunków normalizacji cząstkowej tzn.

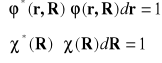
(II-11)

Wówczas

(II-12)

(ponieważ jest to różniczkowanie stałej ) prowadzi do zerowania się pierwszego składnika (II-10) przy obliczaniu wartości własnej energii.

Równanie (II-8) można rozwiązać mnożąc lewostronnie przez
i całkując po zmiennej elektronowej, r. Otrzymujemy

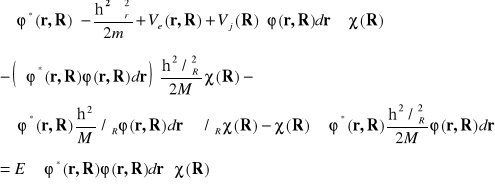
(II-13)

Korzystając z pierwszego warunku normalizacji oraz równania (II-12) otrzymamy

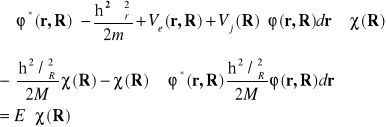
(II-14)

Jeśli założymy, że

to równanie (II-14) da się przekształcić do postaci:

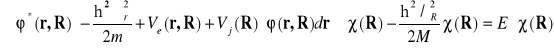
(II-15)

Korzystając dalej z równania (II-5) otrzymamy równanie Schrödingera opisujące ruch jonów

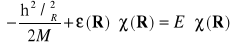
(II-16)

Podsumowując tą część wykładu można powiedzieć , że przybliżenie adiabatyczne pozwala separować ruch elektronów i ruch jonów. Otrzymujemy dwa równania. Najpierw rozwiązujemy równanie (II-5) otrzymując energie elektronów w polu nieruchomych jąder dla każdego położenia jąder osobno. Następnie rozwiązuje się równanie (II-16) otrzymując energie całego układu.

Zwróćmy uwagę co składa się energię
. Równanie (II-5) pozwala na przedstawienie tej energii w formie sumy

(II-17)

gdzie
jest energią elektronu , wartość własna otrzymana z równania Schrödingera nie uwzględniającego potencjału wzajemnego oddziaływania jąder.

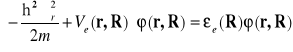
(II-18)

Aby zilustrować powyższe rozważania wykonajmy przykładowe obliczenia . Spróbujmy zanalizować równanie (II-17). Zastanówmy się jak od położeń jąder zależeć będzie energia
w elektronowym stanie podstawowym . Jeśli układ znajduję się w położeniu równowagi jakiekolwiek przesunięcia jonów powodują wzrost energii układu. Z mechaniki klasycznej wiadomo, że możemy wówczas przybliżyć energię układu przy pomocy energii sprężystej. W przypadku gdy układ daje się opisać przy pomocy jednej współrzędnej R

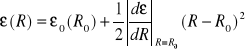
(II-19)

Jak widać jest to rozwinięcie funkcji energii w szereg potęgowy względem położenia równowagi jonów, R=R₀, przy założeniu ,że pierwsza pochodna jest równa zeru (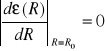
). Łatwo pokazać, że

(II-20)

Łatwo zauważyć, że wykres zależności energii od położeń jąder jest dany przez parabolę. Można wprowadzić nową zmienną Q=R-R₀ wówczas równanie (II-19) można przedstawić w postaci:

(II-21)

Równanie (II-16) jest więc po prostu równaniem oscylatora harmonicznego ( patrz wykład z fizyki teoretycznej lub mechaniki kwantowej)

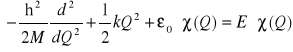
(II-22)

W przypadku, gdy układ elektronów zostanie wzbudzony do wyższych stanów energetycznych warunek (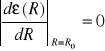
) nie musi być spełniony . Równanie opisujące zależność energii elektronów od położenia jonów w stanie wzbudzonym dane będzie wzorem:

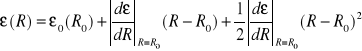
(II-23)

lub

(II-24)

Stała V może być liczona jako

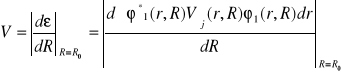
(II-25)

gdzie
elektronową funkcja falową układu w stanie wzbudzonym . Zauważmy, że jeśli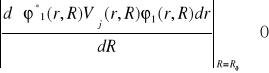
, nawet jeśli w stanie podstawowym

.

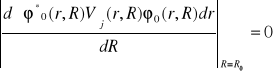
Na rysunku 2 przedstawione są krzywe opisujące energie układu w stanie podstawowym i wzbudzonym . Widać, że po wzbudzeniu do stanu „1” następuje relaksacja jonów do nowego położenie równowagi Q₁.

Elementarna matematyka pozwala obliczyć położenie równowagi jonów w elektronowym stanie wzbudzonym :

(II-26)

oraz związane z przesunięciem jonów obniżenie energii układu

(II-27)

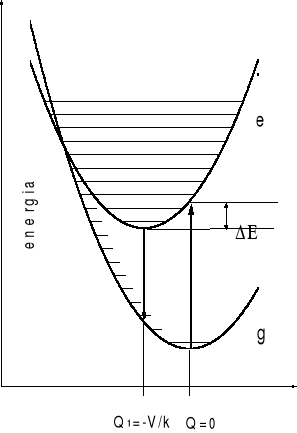
Rysunek 2

Diagram konfiguracyjny . Na rysunku przedstawiono stan podstawowy i jeden ze stanów wzbudzonych. Poziomy oscylacyjne związane z każdym stanem elektronowym przedstawiono przy pomocy linii poziomych .

Wibronowe funkcje falowe maja postać

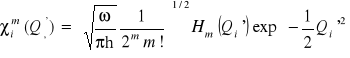
gdzie

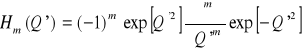
i

Prawdopodobieństwo przejścia jest proporcjonalne do kwadratu momentu przejścia

W niskiej temperaturze widmo emisji dane jest przez przejścia ze stanu poczatkowego

Wówczas kolejne linie będą miały natężania

Analogicznie będzie w przypadku absorpcji . Stanem początkowym będzie stan
a prawdopodobieństwa przejść do kolejnych stanów wibracyjnych wzbudzonego stanu elektronowego będą dane wzorem

gdzie
oznacza liczbę fononów , która mieści się w energii relaksacji sieci

Ptra rysune 2.

Widmo absorpcji i emisji przedstawione jest na rysunku 3.

1

8

---