Wydział Mechaniczny Technologiczny Dzień: 19.04.2002

Kierunek: AiR

Grupa dziekańska: 5

Semestr: 2

LABORATORIUM MECHANIKI OGÓLNEJ

Badanie ruchu płaskiego ciała sztywnego z wykorzystaniem wahadła Maxwella

Sekcja nr 2

• Łukasz Gordel

• Przemysław Lamch

• Piotr Borowik

• Szymon Kosieniak

• Mariusz Fornal

• Paweł Matunin

Cel ćwiczenia

Celem ćwiczenia jest badanie prawa zachowania energii mechanicznej w zamkniętym układzie zachowawczym na przykładzie ciała sztywnego poruszającego się ruchem płaskim. Do tego celu wykorzystane zostało wahadło Maxwella.

Podstawy teoretyczne

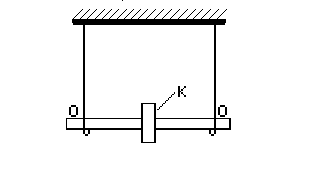
Wahadło Maxwella jest to krążek K osadzony na cienkiej osi. Do obu końców tej osi przywiązane są dwie nici, na których zawieszone jest wahadło. Obracając krążek w palcach nawijamy nici na oba końce osi, poczym badany układ uwalniamy. Zaczyna on powoli spadać, a odwijając się z nici nabiera coraz większej prędkości liniowej i obrotowej. W najniższym położeniu krążek osiąga największą prędkość w ruchu obrotowym i ponownie zaczyna nawijać się na nici.

Złożenie dwóch ruchów, jakie wykonuje krążek, tj. ruch postępowego i obrotowego nazywa się ruchem płaskim.

W zjawisku tym możemy zaobserwować zamianę energii potencjalnej E_p krążka, którą zyskał on dzięki podniesieniu na wysokość h na energię kinetyczną E_k. Z prawa zachowania energii mechanicznej w zamkniętym układzie zachowawczym wynika równość obu form energii, czyli:

E_p = E_k, gdzie :

E_p - energia potencjalna układu w położeniu najwyższym (energia kinetyczna jest równa zero)

E_k - energia kinetyczna układu w najniższym położeniu krążka (energia potencjalna jest rów

na zero).

Ponieważ krążek wykonuje jednocześnie ruch postępowy i ruch obrotowy, energia kinetyczna układu jest sumą energii kinetycznej ruchu postępowego E_kp i energii kinetycznej ruchu obrotowego E_ko : E_p = E_kp + E_ko ,

co dla E_p = mgh, oraz dla E_kp= ˝ mv² daje nam :

2gh v_k²

I = m( - )

ω_k² ω_k²

Masę krążka K można zmieniać poprzez nałożenie na jednego z trzech dołączonych do przyrządu pierścieni P, zmieniając w ten sposób warunki pomiaru. Do doświadczalnego wyznaczenia momentu bezwładności bryły wykorzystuje się zależność powyżej, która po przekształceniu ma postać :

2gh

I= ¼ mD² ( -1)

v_k²

Mierząc wielkości m, D, h, oraz t można w sposób eksperymentalny wyznaczyć moment bezwładności. Dla badanego układu można go wyznaczyć również teoretycznie.

Moment bezwładności osi I_o w kształcie walca względem osi geometrycznej ma postać :

I_o = ⅛ m_oD_o² ,

gdzie : m_o - masa osi,

D_o - średnica zewnętrzna osi.

Moment bezwładności krążka I_k względem osi geometrycznej określa wzór :

I_k = ⅛ m_k (D_k² + D_o²),

gdzie : m_k - masa krążka,

D_k - średnica zewnętrzna krążka.

Podobny wzór określa moment bezwładności pierścienia I_p względem osi geometrycznej :

I_p = ⅛ m_p (D_p² + D_k²),

gdzie : m_p - masa pierścienia,

D_p - średnica zewnętrzna pierścienia.

Moment bezwładności bryły sztywnej wahadła Maxwella jest sumą wyżej wymienionych momentów bezwładności :

I = I_o+ I_k +I_p .

Masę badanego układu wyznacza się z zależności :

m = m_o +m_k +m_p .

Średnia wartość czasu t wyraża się wzorem :

t = ¹/n ∑t_i ,

a błąd względny pomiaru momentu bezwładności otrzymujemy z zależności :

(I - I_t)

δ = 100%

I_t

Dlatego że krążek wykonuje jednocześnie ruch postępowy i ruch obrotowy, energia kinetyczna układu jest sumą energii kinetycznej ruchu postępowego E_kp i energii kinetycznej ruchu obrotowego E_ko. Stąd wzór:

E_p = E_ko +E_kp

Co dla E_p = mgh, E_kp=
mv
, E_ko=
Iω
daje następującą zależność:

I=m(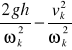
)

Dla celów naszego ćwiczenia wyznaczamy masę całego układu korzystając ze wzoru:

m = m_o+m_k+m_p

m_o czyli masa osi wynosi 0,034 [kg]

m_k czyli masa krążka wynosi 0,123 [kg]

Masę krążka K można zmieniać poprzez nałożenie jednego z trzech dołączonych do przyrządu pierścieni P. Dlatego też w naszym ćwiczeniu policzymy trzy masy układu dla każdego z trzech pierścieni.

Masy poszczególnych krążków(m_k) wynoszą:

1. 0.391 [kg]

2. 0,52 [kg]

3. 0,251 [kg]

Co po podstawieniu daje następujące masy układu:

Dla 1 krążka m=0,574 [kg].

Dla 2 krążka m=0,677 [kg].

Dla 3 krążka m=0,408 [kg].

By uzyskać energię potencjalną podnosimy krążek na pewna wysokość h. W naszym przypadku wynosi ona 0,22 [m]. Należy także zmierzyć średnicę zewnętrzną osi wraz z nawiniętą na nią nicią - D. Wynosi ona 0,0011 [m].

Po wyzerowaniu i uwolnieniu układu, a następnie jego zatrzymaniu odczytujemy z milisekundomierza wielkość czasu spadania wahadła. Czynność tą przeprowadzamy po dziesięć razy dla każdego z pierścieni. Otrzymane wyniki wpisujemy w protokół. Następnie z otrzymanych wyników wyznaczamy średnią wartość czasu t:

[s]

gdzie: n -ilość wykonanych pomiarów

t_i -otrzymana wielkość

Co po podstawieniu daje dla:

1 pierścienia -

1,724 [s]

2 pierścienia -

[s]

3 pierścienia -

[s]

Dla przeprowadzenia ćwiczenia musimy określić również średnice pierścieni, osi i krążka.

Średnica dla każdego z pierścieni jest taka sama i wynosi 0,109 [m], średnica krążka 0,091 [m], a średnica osi 0,0011 [m].

Gdy już zebraliśmy określane dane możemy określić moment bezwładności pierścieni, krążka oraz osi.

Wzór na moment bezwładności osi I_o przedstawia się następująco:

I_o =
[kgm²]

gdzie:

m_o- masa osi,

D_o-średnica zewnętrzna osi,

Co po podstawieniu:

I_o =
=4,25·10^-9 [kgm²]

Wzór na moment bezwładności krążka I_k:

I_k =
[kgm²]

m_k- masa krążka,

D_k-średnica zewnętrzna krążka,

D_o-średnica zewnętrzna osi,

Co po podstawieniu:

I_k =
=1,2733575·10^-4 [kgm²]

Wzór na moment bezwładności pierścienia I_p:

I_p =
[kgm²]

gdzie:

m_p-masa pierścienia,

D_p-średnica zewnętrzna pierścienia,

D_k-średnica zewnętrzna krążka,

Co po podstawieniu:

-dla 1 pierścienia:

=9,828975·10^-4[kgm²]

-dla 2 pierścienia:

=1,13053·10^-3[kgm²]

-dla 3 pierścienia:

=6,3258275·10^-4 [kgm²]

Następnie wynaczamy moment bezwładności I_t dla trzech pierścieni:

I_t = I_o + I_k + I_p [kgm²]

gdzie:

I_o - moment bezwładności osi,

I_k- moment bezwładności krążka,

I_p- moment bezwładności pierścienia,

Co podstawieniu:

- dla 1 pierścienia :

I_t = 4,25·10^-9+1,2733575·10^-4+9,828975·10^-4[kgm²]=1,1102417·10^-3[kgm²]

- dla 2 pierscienia

I_t = 4,25·10^-9+1,2733575·10^-4+1,13053·10^-3[kgm²]=1,2578742·10^-3[kgm²]

- dla 3 pierścienia

I_t = 4,25·10^-9+1,2733575·10^-4+6,3258275·10^-4 [kgm²]=7,5992695·10^-4[kgm²]

Następnie obliczamy moment bezwładności wahadła dla trzech pierścieni korzystając ze wzoru:

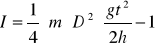
gdzie:

D -średnica zewnętrzna osi mierzona wraz z nawiniętą nicią,

m -masa całkowita układu,

g -przyspieszenie ziemskie,

h -wysokość, na ktorą zostaje podniesiona badana bryła,

Co po podstawieniu :

- dla 1 pierścienia :

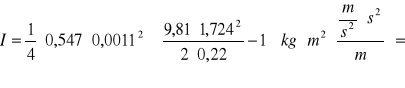
1,079940432·10^-5[kgm²]

- dla 2 pierścienia :

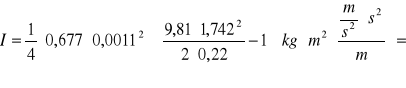
1,365085034·10^-5[kgm²]

- dla 3 pierścienia :

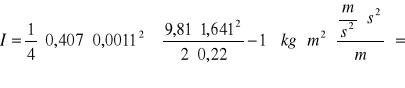
2,512803411·10^-5[kgm²]

Teraz wyznaczamy błąd względny pomiaru momentu bezwładności z zależności:

Co po podstawieniu:

- dla 1 pierścienia :

- dla 2 pierscienia:

- dla 3 pierscienia:

Wnioski:

a)Na dokładność wpływu ma:

- wypoziomowaniu przyrządu (przyrząd źle wypoziomowanych nie pozwala na wykonanie dokładnych pomiarów, ponieważ sznurek z obu stron osi nie jest rozwijany równomiernie, co powoduje znaczne różnice w czasie ruchu postępowego wahadła;

-dokładność nawinięcia sznurka na oś, szybkość opadania obu stron osi nie jest taka sama co powodujeznaczne różnice w wynikach pomiarów;

-niewłaściwe ustawienie dolnej fotokomórki powoduje niedokładność wyników tzn. że czas zmierzony jest krótszy od rzeczywistego czasu spadania wahadła;

-dokładne ustawienie osi wahadła tak, aby sznurek po obu stronach osi równy, ponieważ niewłaściwe ustawienie osi spowoduje nierównomierne „opadanie” wahadła,

b)W pomiarach uwzględniona została grubość nici zawieszenia. Jest to ważny czynnik przy obliczaniu momentu bezwładności, ponieważ nawinięcie na oś sznurka powoduje zwiększenie średnicy zewnętrznej osi. Dla odpowiednio grubej nici nieuwzględnianie jej przy pomiarze średnicy zewnętrznej osi może spowodować, że pomiar będzie szeroko niedokładny. Jednocześnie w niektórych przypadkach grubość nici można pominąć. Można tak postąpić dla niewielkiej grubości nici zawieszenia i dużej średnicy zewnętrznej samej osi. Wówczas błąd pomiarowy będzie pomijalnie mały. Podobnie w przypadku gdy wyznaczamy moment bezwładności dla całej bryły i jest spełniony powyższy warunek. Wówczas pominięcie grubości nici nie wpłynie w sposób znaczący na wynik pomiaru (np.w przypadku jak w ćwiczeniu: nić była dosyć cienka, przez co pominiecie jej w pomiarze średnicy nie spowodowałoby wypaczeniu wyniku). Jednocześnie zauważyć można, że ponieważ średnica i masa osi były stosunkowo niewielkie, to moment bezwładności osi (razem z nicią) był o 10³ mniejszy od momentu zarówno osi jak i pierścienia, czyli pominięcie tego wymiaru nie miało by wielkiego znaczenia(pomimo tego, że średnica występuje we wzorze niż moment bezwładności krążka). Jednak, aby mieć pewność, że pomiar został wykonany dokładnie należy grubość nici zawsze uwzględnić.

c)Aby zwiększyć dokładność pomiaru, należy:

-często sprawdzać czy nici zawieszenia wahadła są po obu równe,

-ustawić dolną fotokomórkę w prawidłowej pozycji,

-starannie wypoziomować przyrząd.

---