Wykład 4
Rozkład funkcji właściwej na ułamki proste
Zasadnicze twierdzenie algebry
Wielomian dowolnego stopnia można rozłożyć na czynniki stopnia co najwyżej 2-go, czyli
(1) ![]()
![]()
![]()
![]()
gdzie ![]()
, ![]()
, ![]()
TW. (o rozkładzie)
Niech ![]()
będzie właściwą funkcją o mianowniku postaci (1).
Wtedy
![]()
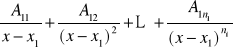
+
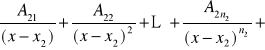
………………………………………
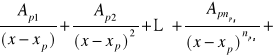
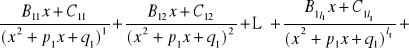
…………………………………………………………
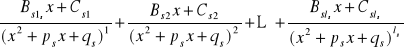
Przykład. Rozłożyć na ułamki proste funkcję ![]()
Ponieważ ![]()
, to
![]()
Mnożymy przez wspólny mianownik ![]()
. Otrzymujemy wówczas
![]()
![]()
Porównujemy współczynniki przy odpowiadających potęgach
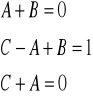
Rozwiązując układ równań otrzymujemy
![]()
, ![]()
, ![]()
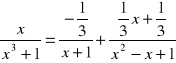
.
Wykład 5
Całka oznaczona
Podział odcinka
Podziałem odcinka ![]()
na ![]()
części nazywamy zbiór ![]()
punktów
![]()
takich, że ![]()
.
Oznaczymy przez ![]()
- długość i-tego odcinka podziału ![]()
Niech ![]()
oznacza długość największego przedziału podziału ![]()
.
Ciąg ![]()
nazywamy średnicą podziału.![]()
.
Podział nazywamy normalnym, jeżeli ![]()
.
Punkt ![]()
nazywamy punktem pośrednim ![]()
tego odcinka podziału![]()
.
Przykład 1. Znaleźć współrzędne punktów podziału ![]()
, długość i -tego odcinka oraz średnicę podziału, jeżeli odcinek ![]()
dzielimy na n równych części
Przykład 2. Znaleźć współrzędne punktów podziału ![]()
, długość i -tego odcinka oraz średnicę podziału, jeżeli odcinek ![]()
dzielimy na 6 części w ten sposób, że punkty podziału tworzą ciąg geometryczny
Def. 1. ( sumy całkowej)
Niech funkcja ![]()
będzie określona i ograniczona na ![]()
oraz niech![]()
będzie podziałem tego odcinka.
Sumą całkową funkcji![]()
odpowiadającą podziałowi![]()
oraz punktom pośrednim ![]()
, gdzie ![]()
tego podziału nazywamy liczbę
![]()
=![]()
Interpretacja geometryczna sumy całkowej
Suma całkowa jest przybliżeniem pola obszaru ograniczonego wykresem funkcji ![]()
, osią ![]()
i prostymi ![]()
Def.2. (całki oznaczonej)
Niech ![]()
będzie ograniczona na![]()
. Jeżeli istnieje granica właściwa ciągu ![]()
niezależna od sposobu podziału ![]()
przedziału ![]()
oraz niezależna od wyboru punktów pośrednich ![]()
, ![]()
, to granicę tę nazywamy całką oznaczoną z funkcji ![]()
na przedziale ![]()
i oznaczamy następująco
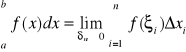
Ponadto przyjmujemy z definicji
(1)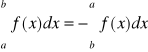
(2) 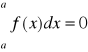
(3) 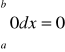
Def.3 Jeżeli istnieje 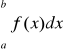
, to funkcję ![]()
nazywamy całkowalną
Każda funkcja całkowalna jest ograniczona, ale nie każda funkcja ograniczona jest całkowalna.
Tw. 1. Funkcja ciągła na ![]()
jest na nim całkowalna..
Przykład 3. Obliczyć na podstawie def. ![]()
Przykład 4. Obliczyć na podstawie definicji ![]()
Z definicji całki oznaczonej wynika następująca interpretacja geometryczna całki oznaczonej
Jeśli ![]()
oznacza trapez krzywoliniowy ograniczony wykresem ciągłej nieujemnej funkcji ![]()
, osią ![]()
oraz prostymi ![]()
, to pole ![]()
trapezu krzywoliniowego wyraża się wzorem
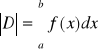
Jeżeli ![]()
., to 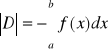
Własności całek oznaczonych
Tw.2 ( o liniowości całki oznaczonej)
Jeżeli ![]()
są całkowalne , to
(1) 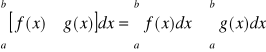
(2) 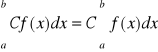
.
Tw. 3 (addytywność całki względem przedziałów całkowania)
Jeżeli ![]()
jest całkowalna na ![]()
oraz ![]()
, to
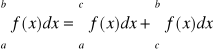
Tw. 4. ( o zachowaniu nierówności przy całkowaniu)
Jeżeli (1)![]()
są całkowalne na ![]()
(2) ![]()
dla każdego ![]()
, to
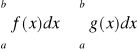
.
Tw.5. ( o wartości średniej)
Jeżeli ![]()
jest ciągła na ![]()
, to
![]()
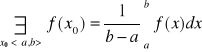
.
Def. 4. Liczbę 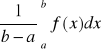
nazywamy wartością srednią.
Dwa podstawowe twierdzenia rachunku całkowego.
Tw. 6 (całka jako funkcja górnej granicy całkowania)
Jeżeli funkcja ![]()
jest ciągła na ![]()
, to funkcja ![]()
określona wzorem
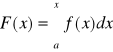
, gdzie ![]()
ma w każdym punkcie przedziału ![]()
pochodną ![]()
.
Tw.7. (związek miedzy całką oznaczoną i nieoznaczoną)
Jeżeli
(1) ![]()
jest ciągła na ![]()
(2) ![]()
jest dowolna funkcją pierwotną funkcji ![]()
na![]()
, to
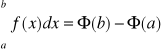
Dowód tw.6.
Ponieważ funkcja ![]()
jest ciągła , to ![]()
ma funkcję pierwotną.
Niech 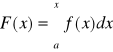
, to 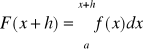
. ![]()
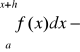
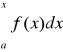
=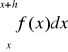
Z tw. o wartości średniej wynika, ze 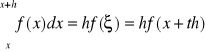
, gdzie ![]()
,czyli ![]()
, ![]()
.
Zatem ![]()
. Ostatnia równość wynika z ciągłości funkcji.
Dowód tw 7.
Niech ![]()
jest dowolną funkcją pierwotną ![]()
. Zdefiniowana w tw.6. ![]()
jest również funkcją pierwotną ![]()
. W takim razie
![]()
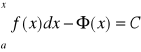
.
Jeśli ![]()
![]()
, to 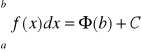
. Jeśli ![]()
, to ![]()
. Stąd wynika teza twierdzenia.
Tw.8. (o całkowaniu przez części)
Jeżeli funkcje ![]()
maja ciągłe pochodne na ![]()
, to
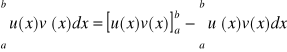
Tw.9. ( o całkowaniu przez podstawianie)
Jeżeli
funkcja
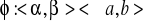
ma ciągłą pochodną na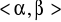
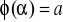
,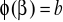
Funkcja
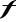
jest ciągła na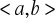
,
to
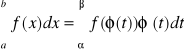
Wyszukiwarka