LABOLATORIUM FIZYKI I |
Ćwiczenie nr :29 |
|||
Wydział: MCHTR |
Grupa: 22 |
Zespół: 7 |
Data: 20.11.2007 |
|
Nazwisko i imię: Arkadiusz Chłystek |
Punktacja: |
Przygotowanie
|
||
Temat ćwiczenia: Optyczna analiza widmowa |
|
|
||
|
|
Sprawozdanie:
|
||
Prowadzący: Michał Ćwil |
|
Suma punktów:
|
||
SPRAWOZDANIE
Cel ćwiczenia
Celem ćwiczenia było zapoznanie się ze zjawiskiem widmowym promieniowania widzialnego. Podczas wykonywania ćwiczenia analizowaliśmy widma takich gazów jak: neon, wodór, krypton, rtęć oraz widmo światła emitowanego przez lampę sodowa.
Promieniowanie elekromagnetyczne - emitowane jest samorzutnie przez ciało ogrzane do odpowiednio wysokiej temperatury, naświetlone promieniowaniem o odpowiednio długiej fali, bądź też poddane wyładowaniu elektrycznemu. Promieniowanie to jest widzialne gdy zawiera się w pewnym zakresie długości fali (od 380[nm] do ok. 780[nm]).
Widmo - zależność obserwowanego natężenia promieniowania od długości fali. Każdy pierwiastek z układu Mendelejewa można doprowadzić do stanu gazowego, którego to widmo jest „widmem liniowym”, obserwowanym w postaci barwnych prążków na ciemnym tle. Każdy taki pierwiastek posiada własnym charakterystyczny tylko dla siebie układ prążków, wynikający z różnych poziomów energetycznych jego atomu. Znajomość tych widm liniowych różnych pierwiastków jest podstawą analizy widmowej.
2. Stanowisko pomiarowe
Obserwację widma umożliwia spektroskop optyczny. Przed szczeliną spektroskopu znajdują się przezroczyste „rurki Geisslera - Plückera”, każda zawiera inny gaz (dla naszego stanowiska są to: rtęć, neon, krypton i wodór). Ustawiając rurkę z badanym gazem na wprost szczeliny, za pomocą wysokiego napięcia doprowadzonego do rurki, gaz zostaje wzbudzony i zaczyna emitować promieniowanie elektromagnetyczne. Światło wysłane przez szczelinę do wnętrza spektroskopu, gdzie ulega rozszczepieniu na pryzmacie lub ugięciu na siatce dyfrakcyjnej (zależnie od typu urządzenia). Elementy optyczne spektroskopu powinny przepuszczać promieniowanie badanego gazu z możliwie najmniejszymi stratami. Na ekranie spektroskopu ukazuje się obraz prążków dyfrakcyjnych. Przy pomocy wyskalowanego pokrętła obraz widma można przesuwać ustawiając wskazówkę ekranu nad pożądanym prążkiem, wówczas ilość działek odczytana ze skali urządzenia, odpowiada długości fali wycentrowanego na wskazówce prążka. Działki na urządzeniu mają wielkość bezwymiarową. Aby dowiedzieć się jakiej długości fali odpowiadają, musimy wyskalować urządzenie. Dokonamy tego przy pomocy rurki z parami rtęci, przyporządkowując długości fali odpowiednim wskazaniom spektroskopu.
Przebieg ćwiczenia
Skalowanie spektroskopu. W tym celu umieszczamy odpowiednią rurkę na przeciw szczeliny spektroskopu, podłączamy wysokie napięcie do rurki wzbudzając gaz. Przyporządkowując ilości działek na dany prążek (ze skali urządzenia) odpowiadającą mu długość fali (z tablicy katalogowej) wyskalujemy urządzenie pomiarowe.
Wykres. Za pomocą programu komputerowego, narysować wykres otrzymanej zależności długości fali od wskazania spektroskopu i dopasować do niego odpowiednia krzywą drugiego stopnia.
Pomiary widm innych gazów. Wykonać pomiary długości fal odpowiadających liniom widm emisyjnych gazów (neon, krypton i wodór) przy pomocy krzywej skalowania oraz ocenić intensywność prążków.
na podstawie krzywej skalowania ocenić czy za pomocą spektroskopu można zaobserwować dublet sodowy.
zmierzyć długość fal odpowiadających prążkom dubletu sodowego.
określić błąd pomiaru jako różnicę odczytywanych długości fal dla przesunięcia skali spektroskopu o wartości połowy odległości miedzy działkami
Wyniki pomiarów
Widmo rtęci
Skala spektrometru (odczyt) |
Kolor linii widma |
λ [nm] (z tabeli) |
Poziom Natężenia |
31,5 |
Fioletowy |
435,8 |
5 |
61,8 |
Niebieski |
491,6 |
2 |
91,3 |
Zielony |
546,1 |
5 |
100,9 |
Żółty |
577,0 |
3 |
101,6 |
Żółto-pomarańczowy |
579,1 |
3 |
125,2 |
Czerwony |
690,8 |
1 |
129,2 |
|
698,1 |
1 |
Korzystając faktu, że znamy długości fali dla odpowiednich kolorów prążków (dane z tabeli) Wprowadziliśmy dane do programu Origin i stworzyliśmy wykres zależności długości fali od działki stetoskopu . Wykres umieszczam poniżej
Y = A + B1*X + B2*X^2
Parameter Value Error
------------------------------------------------------------
A 450,10322 6,83776
B1 -1,1756 0,18959
B2 0,02437 0,00123
------------------------------------------------------------
R-Square(COD) SD N P
------------------------------------------------------------
0,99869 2,76669 11 <0.0001
------------------------------------------------------------
Korzystając z odpowiedniej funkcji programu wpisywaliśmy wartość odczytaną na narzędziu pomiarowym i otrzymywaliśmy odpowiednie długości fali. Wyniki obrazują następujące tabele:
II. Widmo neonu
Skala spektrometru (odczyt) |
Kolor linii widma |
λ [nm] (odpowiadające) |
Poziom natężenia |
30,4 |
Fioletowy |
437,0 |
1 |
56,6 |
Niebieski |
463,6 |
3 |
73,9 |
Niebiesko-zielony |
489,5 |
2 |
86,3 |
Zielony |
531,9 |
3 |
86,7 |
Zielony |
533,1 |
3 |
88,9 |
Zielony |
539,9 |
4 |
103,3 |
Żółty |
589,3 |
5 |
104,1 |
Pomarańczowo - żółty |
592,3 |
3 |
109,5 |
Pomarańczowy |
613,6 |
4 |
110,6 |
Pomarańczowy |
618,0 |
5 |
118,4 |
Czerwony |
651,4 |
3 |
III. Widmo kryptonu
Skala spektrometru (odczyt) |
Kolor linii widma |
λ [nm] (odpowiadające) |
Poziom natężenia |
28,3 |
Fioletowy |
436,2 |
2 |
33,1 |
Niebieski |
445,5 |
1 |
65,0 |
Niebieski |
478,8 |
1 |
94,9 |
Zielony |
559,3 |
3 |
103,9 |
Żółty |
591,6 |
3 |
117,5 |
Czerwony |
565,3 |
1 |
IV. Widmo wodoru
Skala spektrometru (odczyt) |
Kolor linii widma |
λ [nm] (odpowiadające) |
Poziom natężenia |
29, |
Fioletowy |
436,8 |
2 |
65,0 |
Niebieski |
478,7 |
5 |
119,6 |
Czerwony |
656,7 |
4 |
V. lampa sodowa
Skala spektrometru (odczyt) |
Kolor linii widma |
λ [nm] (odpowiadające) |
Poziom natężenia |
104,2 |
Pomarańczowy |
592,8 |
5 |
104,4 |
Pomarańczowy |
593,5 |
5 |
5. Opracowanie wyników
Obliczenie błędu pomiaru długości fali λ
W Programie Origin dla zależności długości fali od wartości działki spektrometru przyporządkowaliśmy parabolę. Otrzymaliśmy wzór funkcji, która opisuje tą zależność:
![]()
Na błąd pomiaru składa się błąd systematyczny ( błąd igły + błąd podziałki) i błąd przypadkowy:
Błąd igły : 5 działek w skali stetoskopu , błąd odczytu : 0,5 działki elementarnej, co nam daje:
Δa=0,55 działki w skali stetoskopu,
Błąd całkowity:
![]()
Korzystając z tych zależności obliczamy długość fali wraz z błędem pomiaru. Długości fali otrzymaliśmy wprowadzając wartości działki do programu Origin. Wartości błędu obliczę korzystając z formularza Excel. Poniższe tabele obrazują wyniki:
I. Widmo neonu
Skala spektrometru (odczyt) |
λ [nm] (odpowiadające) |
Δ λ [nm] |
30,4 |
437,0 |
0,239114 |
56,6 |
463,6 |
0,112058 |
73,9 |
489,5 |
0,343939 |
86,3 |
531,9 |
0,510142 |
86,7 |
533,1 |
0,515503 |
88,9 |
539,9 |
0,544991 |
103,3 |
589,3 |
0,738002 |
104,1 |
592,3 |
0,748724 |
109,5 |
613,6 |
0,821103 |
110,6 |
618,0 |
0,835847 |
118,4 |
651,4 |
0,940394 |
II. Widmo kryptonu
Skala spektrometru (odczyt) |
λ [nm] (odpowiadające) |
Δ λ [nm] |
28,3 |
436,2 |
0,267261 |
33,1 |
445,5 |
0,202924 |
65,0 |
478,8 |
0,224648 |
94,9 |
559,3 |
0,625412 |
103,9 |
591,6 |
0,746044 |
117,5 |
565,3 |
0,928331 |
III. Widmo wodoru
Skala spektrometru (odczyt) |
λ [nm] (odpowiadające) |
Δ λ [nm] |
29,9 |
436,8 |
0,257879 |
65,0 |
478,7 |
0,224648 |
119,6 |
656,7 |
0,956479 |
IV. lampa sodowa
Skala spektrometru (odczyt) |
λ [nm] (odpowiadające) |
Δ λ [nm] |
104,2 |
592,8 |
0,750065 |
104,4 |
593,5 |
0,752745 |
Obliczanie stałej Rydberga
Odwrotność długości fali wyraża się zależnością:
![]()
, gdzie m=1, 2, 3.. - odpowiada numerowi serii, zaś n=m+1
R- szukana stała Rydberga
Dla serii Blamera:
m=2
n=3,4,5…
Po wprowadzeniu danych do programu Origin otrzymaliśmy odpowiedni wykres
W którym szykaną wartością R jest wartość współczynnika kierunkowego prostej B=1,90194![]()
Wartość błędu przypadkowego ΔR = 6,55375![]()
należy pomnożyć przez współczynnik t-Studenta, ze względu na małą ilość punktów pomiarowych. Wobec tego wartość błędu wynosi:
t= 2,35 dla β=0,9
ΔR = 6,55375![]()
![]()
=15,40131![]()
![]()
36,1931![]()
Błąd systematyczny obliczonej wartości (różniczka zupełna)
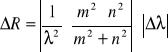
![]()
Więc stała Rydera z naszych doświadczalnych obliczeń wynosi:
R=![]()
![]()
Natomiast R teoretyczne=1,0967758![]()
![]()
Wartości energii odpowiadające prążkom dubletu sodowego
![]()
![]()
![]()
Błąd z różniczki zupełnej :
![]()
h - stała Planca
c- prędkość światła
prążek pierwszy:
λ=592,8[nm]
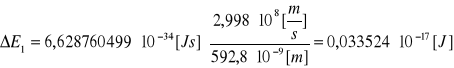
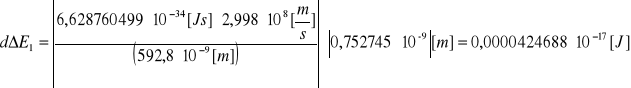
![]()
prążek drugi:
λ=593,5[nm]
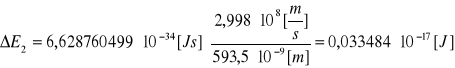
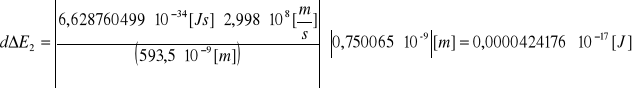
![]()
![]()
, co daje odpowiednio:
![]()
![]()
Wynik z tablic:
![]()
, dla fali o długości 589,3nm
Wnioski
Podczas wykonywania ćwiczenia dowiedzieliśmy się że znając długość fal odpowiadających poszczególnym prążkom widma określonego gazu, za pomocą spektrometru i przybliżenia krzywą drugiego stopnia, możemy obliczyć długości fal odpowiadających poszczególnym prążkom widma dowolnego gazu.
Obliczyliśmy także stałą Rydberga na podstawie linii widma wodoru, zauważyliśmy ze obliczeniowa wartość stałej jest większa od stałej teoretycznej dziesięciokrotnie. Możemy przypuszczać że dokonaliśmy błędu pomiaru lub błędu przy obliczeniach bo to jest wartość niewiarygodna.
Także wartości energii dubletu sodowego (obliczona na podstawie danych zgromadzonych podczas wykonywania ćwiczenia, oraz teoretyczna) są porównywalne .
8
Sprawozdanie z ćwiczenia nr.29
Arkadiusz Chłystek, grupa 22, zespół 7
Wyszukiwarka