Wykonaj działania i przeprowadź redukcję wyrazów podobnych
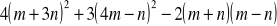
,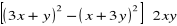
,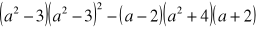
.Udowodnij, że jeśli
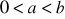
, to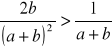
.Oblicz wartość wyrażenia:
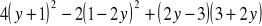
, jeśli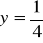
.Oblicz wartość wyrażenia
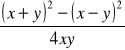
, jeśli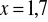
oraz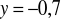
.Dane są liczby
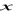
,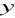
. Oblicz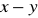
,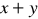
,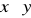
,
, dla: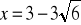
,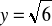
.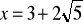
,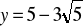
.Rozwiąż równanie:
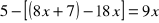
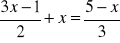
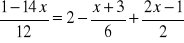
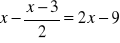
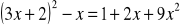
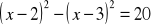
Rozwiąż nierówność:
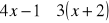
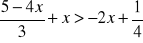
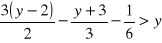
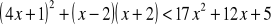
Podaj przykład układu równań oznaczonego, nieoznaczonego i sprzecznego.
Mając dane równanie
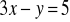
dopisz drugie równanie tak, aby otrzymany układ:posiadał jedno rozwiązanie;
nie posiadał rozwiązań;
posiadał nieskończenie wiele rozwiązań.
Określ liczbę rozwiązań układu (nie rozwiązując układu)
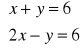
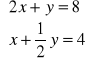
Sprawdź, czy para liczb
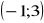
należy do zbioru rozwiązań równania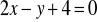
.Sprawdź, czy para liczb
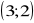
należy do zbioru rozwiązań równania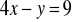
.Sprawdź, czy para liczb
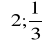
należy do zbioru rozwiązań układu równań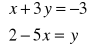
.Rozwiąż układ równań:
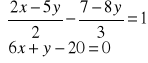
.Rozwiąż algebraicznie i graficznie układ równań. Podaj nazwę układu.
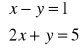
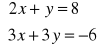
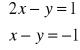
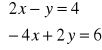
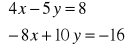
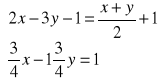
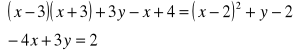
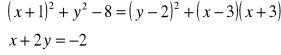
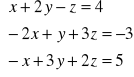
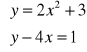
Rozwiąż układ równań
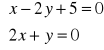
algebraicznie;
graficznie;
określ, czy jest to układ oznaczony, nieoznaczony czy sprzeczny.
Jaki układ równań liniowych nazywamy oznaczonym, nieoznaczonym, sprzecznym? Przeprowadź dyskusję istnienia rozwiązań układu równań
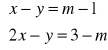
Dla jakich wartości parametru
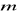
układ równań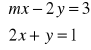
ma rozwiązanie?Przeprowadź dyskusję istnienia rozwiązań układu równań
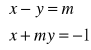
.Rozwiąż układ równań z parametrem
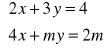
. Przedyskutuj liczbę rozwiązań układu.Długość prostokąta jest o 12 cm większa od jego potrojonej szerokości. Oblicz wymiary prostokąta, jeżeli obwód wynosi 104 cm.
Suma trzech kolejnych liczb nieparzystych wynosi 87. Znajdź te liczby.
Jeżeli na prezenty dla brata wydałem
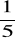
, a dla siostry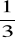
posiadanych pieniędzy, to zostało mi 7 złotych. Ile miałem pieniędzy?Znajdź dwie liczby, których suma jest równa 25, a różnica 9.
Za 2 kg bananów i 3 kg mandarynek zapłacono 14,7 zł, a za 3 kg bananów i 5 kg mandarynek zapłacono 23,4 zł. Ile kosztował 1 kg mandarynek i 1 kg bananów?
Do 2 litrów roztworu o stężeniu
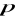
% dolano 3 litry roztworu o stężeniu 20 %. Otrzymano w ten sposób roztwór o stężeniu 15 %. Ile wynosi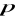
?44 tony towaru przywieziono 9 samochodami o ładowności 4 tony i 6 ton. Ile było samochodów mniejszych, a ile większych, jeżeli każdy został wykorzystany maksymalnie.
Gdyby Aleksander Wielki umarł o 5 lat wcześniej panowałby
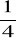
swego życia, gdyby zaś żył o 9 lat dłużej panowałby połowę swego życia. Ile lat żył i ile panował?Uczniowie klasy I f zamierzają wynająć autokar na wycieczkę. Gdyby uczniowie zapłacili po 12 zł 50 gr, to do pokrycia kosztów wynajmu autokaru zabrakłby 100 zł, a jeżeli każdy z uczniów zapłaci po 16 zł, to po opłaceniu kosztów wynajmu autokaru zostanie 12 zł. Ile osób planuje wyjazd na tę wycieczkę? Jaki jest koszt wynajęcia autokaru?
Przy wypłacie jeden z robotników otrzymał o 50 zł więcej niż drugi. Oprócz tego drugi robotnik zwrócił pierwszemu dług w wysokości 600 zł. Okazało się wówczas, że pierwszy robotnik miał 2 razy więcej pieniędzy niż drugi. Ile wynosiła pensja każdego z robotników?
Rozwiąż równanie:
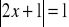
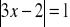
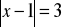
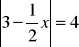
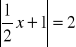
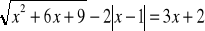
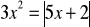
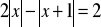
.Uprość wyrażenie:
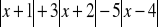
dla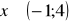
.Rozwiąż nierówność;
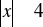
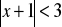
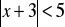
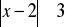
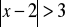
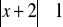
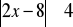
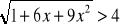
Z podanego wzoru wyznacz wskazaną niewiadomą
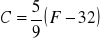
,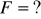
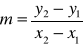
,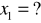
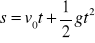
,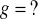
,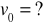
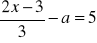
,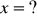
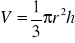
,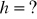
.Rozwiąż równanie:
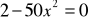
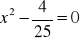
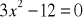
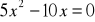
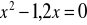
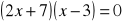
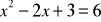
.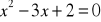
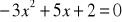
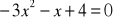
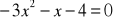
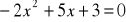
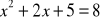
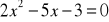
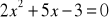
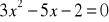
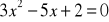
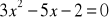
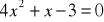
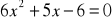
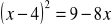
.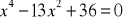
Dla jakich wartości parametru
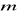
równanie ma dokładnie jeden pierwiastek.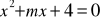
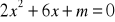
Podaj liczbę różnych pierwiastków równania w zależności od parametru
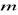
: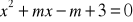
.Korzystając z wzorów Viete'a, oblicz:
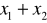
,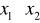
,gdzie
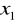
,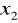
są pierwiastkami równania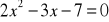
.Rozwiąż równanie z niewiadomą
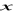
i zbadaj dla jakich wartości parametru równanie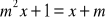
ma dokładnie jedno rozwiązanie, nie ma rozwiązania, jest tożsamościowe.Iloczyn trzeciej i szóstej części pewnej liczby jest równy tej liczbie. Jaka to liczba?
Kwadrat pewnej liczby całkowitej jest równy ośmiokrotności tej liczby. Znajdź tę liczbę.
Suma kwadratów trzech kolejnych liczb nieparzystych jest równa 155. Znajdź te liczby.
Suma kwadratów trzech kolejnych licz naturalnych jest równa 245. Znajdź te liczby.
Suma kwadratów trzech kolejnych liczb naturalnych jest równa 194. Znajdź te liczby.
Iloczyn dwóch kolejnych liczb całkowitych równa się 210. Wyznacz te liczby.
Długość prostokąta jest o 3 m większa od szerokości, a jego pole jest równe 180 m2. Jakie są wymiary tego prostokąta?
Szerokość prostokąta jest o 2 m mniejsza od długości, a jego pole jest równe 288 m2. Jakie są wymiary tego prostokąta?
Długość przekątnej kwadratu jest o 3 cm większa od długości jego boku. Znajdź obwód kwadratu.
Mamy ogrodzić prostokątną działkę, której jeden bok jest o 10 m dłuższy od drugiego. Jaka długa musi być siatka, jeżeli pole powierzchni wynosi 1200 m2?
Złożono do banku 4000 zł na lokatę odnawialną co rok. Po dwóch latach stan lokaty wynosi 4410 zł. Wyznacz stopę procentową tej lokaty zakładając, że była stała.
(*) Suma cyfr pewnej liczby dwucyfrowej wynosi 5. Iloczyn tej liczby i liczby o tych samych, ale przestawionych cyfrach wynosi 736. Zapisz treść zadania w postaci układu równań. Znajdź tę liczbę.
ZADANIA ZAMKNIĘTE
Średnią arytmetyczną liczby
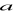
i liczby o 5 od niej większej można zapisać za pomocą wyrażenia: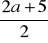
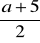
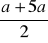
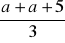
Średnią arytmetyczną liczby
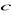
i liczby o 7 od niej mniejszej można zapisać za pomocą wyrażenia: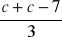
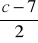
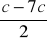
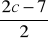
Po przekształceniu wyrażenia
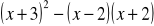
otrzymamy: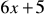
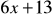
13
5
Po przekształceniu wyrażenia
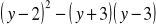
otrzymamy: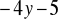
5
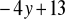
-13
Największa liczba całkowita spełniająca nierówność
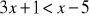
to:-3
-2
-4
-5
Największa liczba całkowita spełniająca nierówność
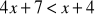
to:-1
-2
0
1
Rozwiązaniem układu równań
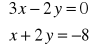
jest:para liczb dodatnich
para liczb ujemnych
jedna liczba dodatnia, druga równa zero
para liczb o różnych znakach
Rozwiązaniem układu równań
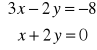
jest:para liczb dodatnich
para liczb o różnych znakach
para liczb ujemnych
jedna liczba dodatnia, druga równa zero
Wyszukiwarka