11.Podaj definicję iloczynu skalarnego, zdefiniuj pracę przy F=const.

iloczyn skalarny
Iloczyn skalarny wektorów a i b oznaczamy symbolicznie a . b. Iloczyn skalarny dwóch wektorów jest skalarem, którego wartość liczbowa jest równa iloczynowi wartości liczbowych danych wektorów przez cosinus kąta zawartego między nimi, czyli:

Praca mechaniczna jest wykonywana wtedy, gdy pod działaniem siły ciało jest przesuwane na pewną odległość.

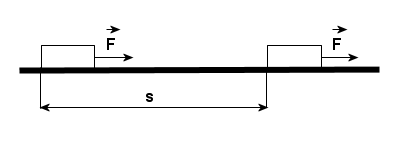
Praca jest większa, gdy wykonuje ją większa siła lub gdy przesunięcie (droga) jest większe.
Wzór na pracę (oznaczaną literą W) z rysunku:

Niech siła F działa na ciało pod kątem α do kierunku ruchu ciała:

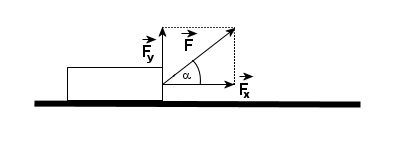
Po rozłożeniu siły F na składowe okazało się, iż pracę wykonuje tylko składowa FX. Z rysunku:

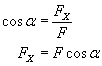
Wykonana praca wynosi więc:

I to jest ostateczny wzór na pracę, gdzie α to kąt między wektorem przesunięcia s a wektorem działającej siły F.
Jednostką pracy w układzie SI jest dżul:

Rozpatrzmy poszczególne przypadki:

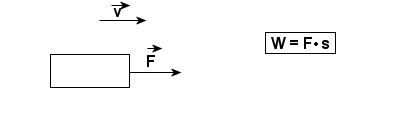
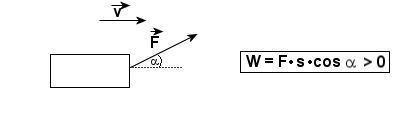
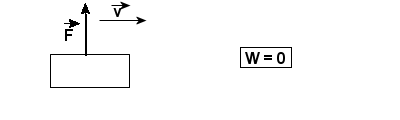
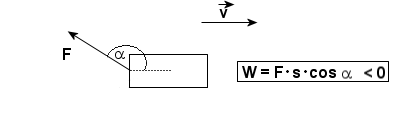
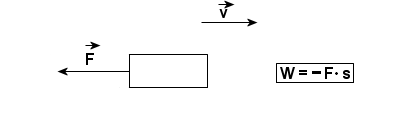
W całym tym dziale zakładamy, że wartość siły F jest stała. F=const.

12. Zdefiniuj siłę tarcia w przypadku ciała znajdującego się na płaszczyźnie poziomej oraz na równi pochyłej.

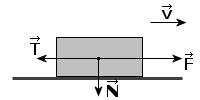
Na ciało poruszające się z prędkością v dzięki sile napędzającej F, działa siła tarcia (dynamicznego) T skierowana przeciwnie do kierunku ruchu. Jak wiemy, zależy ona od siły nacisku N i wyrażamy ją wzorem:

*siła tarcia na równi, patrz zad. 10.

13. Jaką pracę należy wykonać aby przesunąć ciężar Q wzdłuż drogi S po równi pochyłej o kącie nachylenia α względem poziomu. Współczynnik tarcia wynosi f.

Podobnie jak w przypadku z zadania 10. Z tymi różnicami: Siła tarcia skierowana w przeciwnym kierunku. Siła zsuwania jest równa sile wsuwania. Korzystamy ze wzorów:

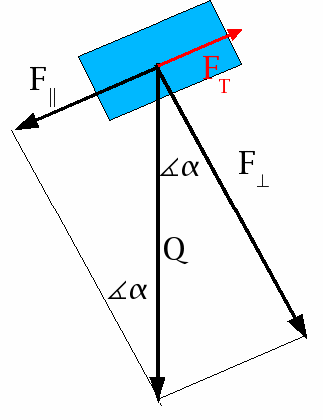
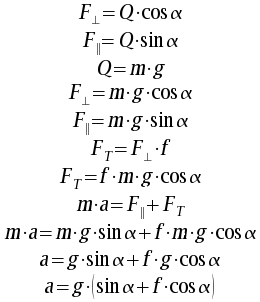
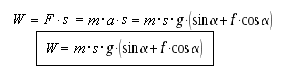
14. Podaj zasadę zachowania energii mechanicznej. Ciało zaczyna spadać z wysokości h. Udowodnij, że jego energia mechaniczna w chwili początkowej jest taka sama jak po przebyciu drogi x.

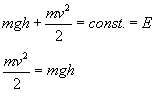
Energia mechaniczna — suma energii kinetycznej i potencjalnej.

Załóżmy że ciało zaczyna spadać, w chwili początkowej nie ma prędkości, czyli energia kinetyczna jest równa 0, a potencjalna E=mgh.

Ciało spada, więc nabiera prędkości, wynika to z przyśpieszenia grawitacyjnego więc V=gt,

więc jego energia kinetyczna wynosi
, a enegia potencjalna po przebyciu drogi x (
) E=mg(h-x).

Po podstawieniu wychodzi że Energia mechaniczna w obydwu przypadkach jest taka sama.

15.Zdefiniuj iloczyn wektorowy.

Iloczynem wektorowym wektorów a i b leżących na jednej płaszczyźnie i pomiędzy kierunkami których jest kąt α, nazywamy wektor c o wartości:

Jeżeli śrubę prawoskrętną ustawioną równolegle do kierunku wektora c obracamy kręcąc wg kolejności mnożonych wektorów - od a do b, to ruch posuwisty śruby (wkręcanie lub wykręcanie) wskazuje zwrot wektora c.

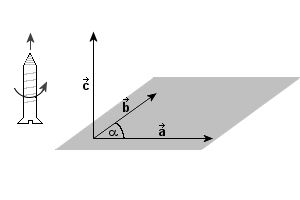
Zauważmy, że o zwrocie wektora c decyduje kolejność mnożenia, czyli jeśli zamienimy kolejność wektorów a i b, otrzymamy wektor przeciwny.

16. Zdefiniuj moment pędu punktu materialnego.

Moment pędu to podstawowa i ważna wielkość fizyczna, związana z ruchem obrotowym ciał wokół osi. Ma ona charakter takiego wektora, który jest wynikiem iloczynu wektorowego wektora odległości ciała od osi i jego wektora pędu.

Ową zależność zapisujemy poniższym wzorem:

L = r x p

gdzie: L - wektor momentu pędu, r - wektor odległości od osi, p - wektor pędu, x - symbol iloczynu wektorowego.

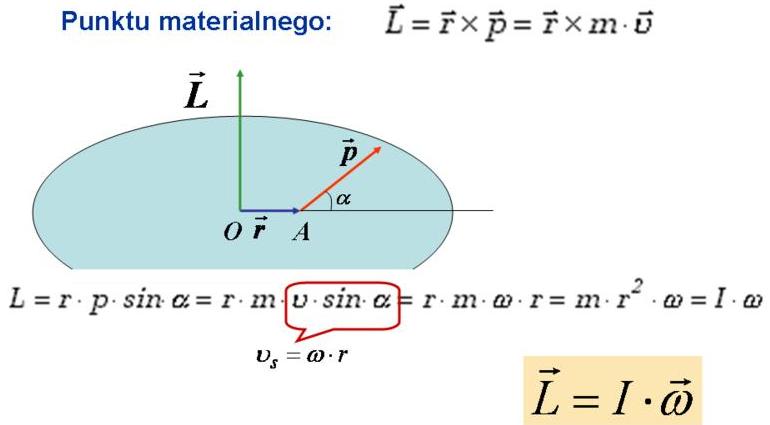
Moment pędu ("L") punktu materialnego:
jest to iloczyn wektorowy "r" i "p".

Czyli:
L = r * p
p = m * V
L = r * m * V

Przy czym "r" to wektor łączący pewien punkt (np. O) z aktualnym położeniem ciała o masie "m", "V" - prędkość z jaką porusza się ciało, "p" - pęd tego ciała.

W wypadku ruchu po okręgu mom. pędu liczymy względem jego środka.
Ogólny wzór to: L = r * m * V * sin"alfa"
Wektor jest prostopadły do ruchu, czyli "alfa" = 90* , a sin"alfa" = 1.
Wtedy L = rmV tylko, że "r" to promień okręgu.


Mom. pędu dla bryły sztywnej:
L = I * w
"I" , czyli moment bezwładności, jest inne dla różnych rodzajów brył (np. inne jest dla walca, inne dla rury cienkościennej itd.)
"w" to prędkość kątowa, w = delta"alfa"/delta t "t" to oczywiście czas

17.Wyprowadź zależność między momentem siły a momentem pędu.

Równanie ruchu obrotowego:

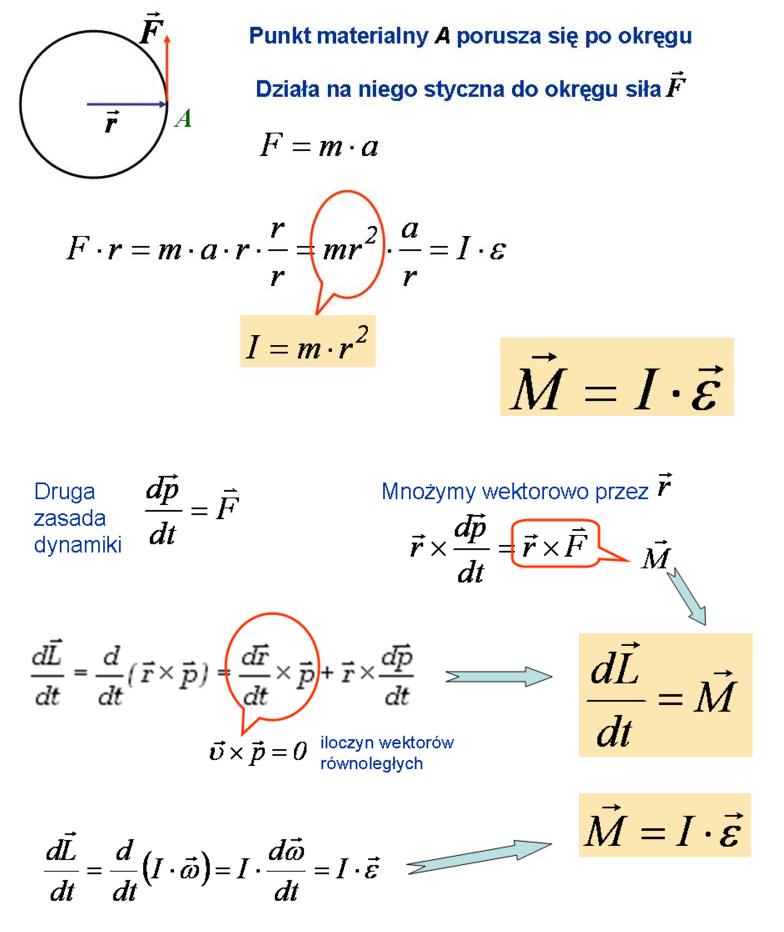
Moment pędu:

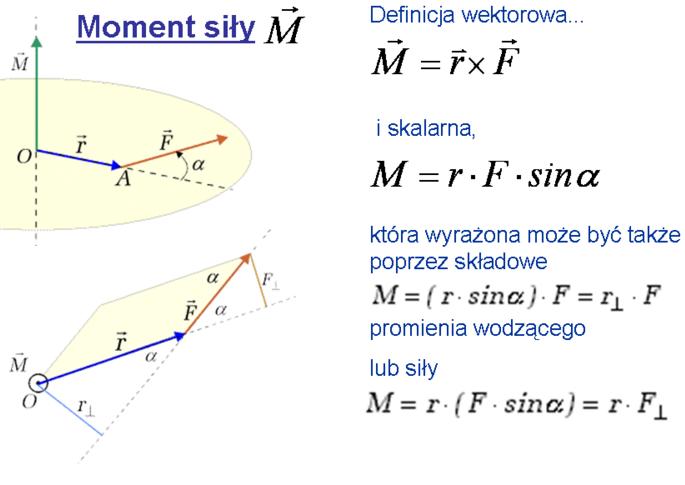
Moment siły:

Moment bezwładności:

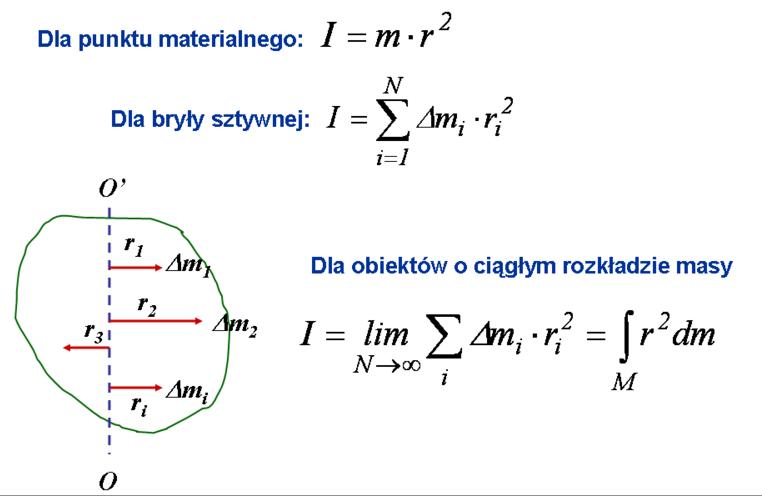
18. Zdefiniuj wektor wodzący środka masy.


Wektor wodzący - wektor łączący początek układu odniesienia z środkiem ciężkości poruszającego się ciała.

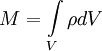
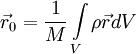
Powyższa zależność dla ośrodków ciągłych, zapisana w postaci wyrażeń całkowych wiąże środek masy z rozkładem gęstości ρ w przestrzeni za pomocą zależności:

• M - masa ciała;

• V - objętość ciała;

• ρ = ρ(x,y,z) funkcja gęstości ciała.

• r-wektor wodzący środka masy

Funkcja gęstości ciała pokrywa się ze środkiem masy.

Gdy ciało wiruje lub drga, istnieje w tym ciele punkt, zwany środkiem masy, który porusza się w taki sam sposób, w jaki poruszałby się pojedynczy punkt materialny poddany tym samym siłom zewnętrznym.

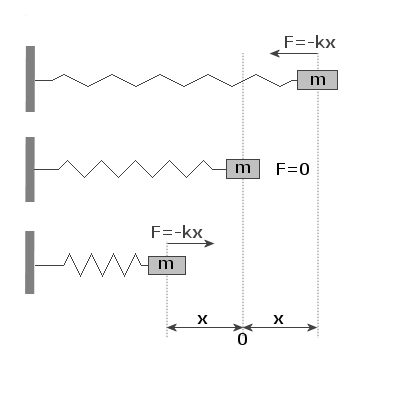
19. Ruch harmonicznie prosty, nietłumiony:
równanie ruchu
energia potencjalna
energia kinetyczna
energia całkowita

Na powyższym rysunku przedstawiony jest prosty oscylator harmoniczny. Jest nim klocek o masie m przyczepiony do sprężyny o stałej sprężystości k. Pierwsza sprężyna jest rozciągnięta, druga jest w stanie równowagi, a trzecia jest ściśnięta. W każdym z trzech przypadków przedstawiona jest siła F, z jaką sprężyna działa na masę m. Zakładamy, że klocek ślizga się po doskonale gładkim poziomym stole.

Stosując drugą zasadę dynamiki Newtona (F = ma), otrzymamy równanie:

-kx=ma
Stałą A nazywamy amplitudą ruchu. Czyli amplituda to inaczej wychylenie maksymalne (równe na naszym rysunku wartości x).

Wielkość (ωt+φ) nazywamy fazą ruchu, przy czym φ jest fazą początkową.
Dwa ruchy mogą mieć te same amplitudy i częstości, lecz różne fazy.

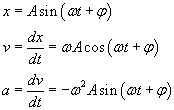
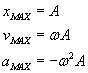
Przy maksymalnym wychyleniu w obydwu kierunkach prędkość równa jest zeru, ponieważ musi wtedy zmieniać kierunek. Przyspieszenie w takiej chwili, podobnie jak siła przywracająca równowagę, osiąga wartość maksymalną, lecz jest skierowane przeciwnie do przemieszczenia. Kiedy wychylenie jest zerowe, prędkość punktu materialnego osiąga maksimum, a przyspieszenie znika, tak jak to się dzieje z siłą przywracającą równowagę. Prędkość wzrasta w miarę zbliżania się punktu materialnego do położenia równowagi i maleje w miarę zbliżania się do maksymalnego wychylenia.

• Energia w ruchu harmonicznym (drgającym)

Energia potencjalna

Ciało drgające ruchem harmonicznym prostym posiada energię potencjalną wtedy, gdy znajduje się ono w jakimś wychyleniu od stanu równowagi. Gdy ciało znajduje się więc w położeniu równowagi, nie posiada energii potencjalnej.
Energia potencjalna jest równa energii potencjalnej sprężystości, którą możemy wyrazić wzorem:

Uwzględniając wzór na wychylenie x, otrzymujemy:

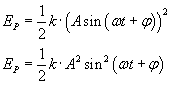
Maksymalna wartość energii potencjalnej wynosi

Energia kinetyczna

Ciało o masie m drgające ruchem harmonicznym prostym posiada energię kinetyczną wtedy, gdy posiada ono jakąś prędkość v w danej chwili. Oznacza to, że ciało nie posiada energii kinetycznej wtedy, gdy prędkość równa jest zeru, a taki moment następuje, gdy ciało znajduje się w położeniu maksymalnego wychylenia (x = A).
Energię kinetyczną wyrażamy wzorem:

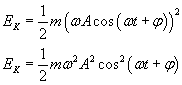
podstawiając za V:

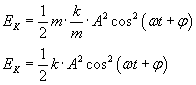
następnie:

Maksymalna wartość energii kinetycznej wynosi:

Mamy z nią do czynienia, gdy drgające ciało ma największą prędkość (a jak wiemy, ma ono ją wtedy, gdy znajduje się w punkcie równowagi x = 0).




Energia mechaniczna-całkowita.

Całkowita energia punktu materialnego poruszającego się ruchem harmonicznym prostym jest proporcjonalna do kwadratu amplitudy tego ruchu.

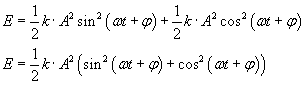
1) siła tarcia zależy od rodzaju powierzchni obu stykających się ciał,
2) siła tarcia nie zależy od wielkości powierzchni styku ciała z podłożem,
3) siła tarcia nie zależy od prędkości ciała
4) siła tarcia jest wprost proporcjonalna do siły nacisku:

---