Dominika Kobiałka 2004-03-02

C3

L5

SPRAWOZDANIE

Z LABORATORIUM Z FIZYKI nr 2

Temat doświadczenia:

Wyznaczanie wartości c_p/c_v dla powietrza metodą Clémenta-Desormesa

Zadaniem nasze polega a tym by doświadczalnie wyznaczy wartość współczynnika Kappa dla powietrza. Współczynnik Kappa zwany również współczynnikiem Poissona to wykładnik adiabaty. Adiabata opisuje prawa przemiany adiabatycznej gazu czyli przemiany podczas której nie zachodzi wymiana ciepła po między układem a otoczeniem. Praktycznie proces adiabatyczny realizuje się przy wystarczająco szybkim rozszerzaniu lub sprężaniu gazu. Warunek adiabatyczności będzie spełniony, jeżeli proces przebiega tak prędko, że nie zdąży zajść wymiana ciepła między układem a otoczeniem. Przy adiabatycznym rozszerzaniu gaz oziębia się. Pracę rozszerzenia gaz wykonuje kosztem ubytku swojej energii wewnętrznej. Gdy pod działaniem sił zewnętrznych gaz ulega adiabatycznemu sprężeniu to jednocześnie ogrzewa się. Przy tym praca wykona przez siły zewnętrzne jest zużyta w całości na zwiększenie zapasu energii wewnętrznej gazu.

W izo - przemianach gazów (przemiany, podczas których jeden z czynników: p - ciśnienie, V - objętość, lub T - temperatura pozostaje stały ), założeniem jest stała masa próbki gazu ulegającego przemianie. Wykładnik adiabaty κ równy jest stosunkowi ciepła właściwego gazu przy ogrzewaniu go pod stałym ciśnieniem (c_p) do ciepła właściwego tego gazu przy ogrzewaniu go przy stałej objętości (c_v). Ponieważ podczas ogrzewania przy stałym ciśnieniu gaz zwiększa swą objętość, a zatem wykonuje pracę, c_p jest zawsze większe od c_v, a więc κ=
będzie zawsze większe od 1. W doświadczeniu naszym jednak masę powietrza zmienialiśmy w celu osiągnięcia konkretnych wyników.

Doświadczalny pomiar wartości κ przeprowadzimy następująco:

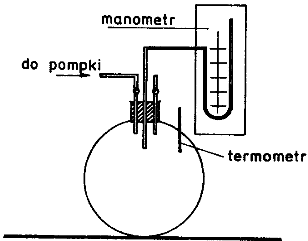
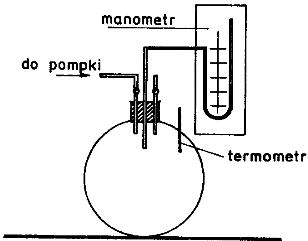
1. Do butli szklanej o dużej pojemności wprowadzamy sprężone powietrze za pomocą pompki do ciśnienia p + p₁, gdzie p oznacza ciśnienie atmosferyczne, a p₁ . Zamykamy zawór, i odczekujemy kilka minut aż do wyrównaniu się temperatury gazu w butli. Po ustaleniu się równowagi pomiędzy temp. butli i otoczenia odczytujemy różnicę wysokości słupa cieczy na manometrze, która jest proporcjonalna do nadwyżki ciśnienia p₁.

2. Spuszczamy powietrze z butli przez otwarcie kurka, po czym kurek zakręcamy. Tak

3. Biorąc pod uwagę krótki czas potrzebny na zejście powietrza z butli, możemy założyć, że zaszła przemiana adiabatyczna. Warunek adiabatyczności został spełniony ponieważ powietrze zostało wprowadzone oraz u

4. Czekamy na wyrównanie się temperatury w butli z temperaturą otoczenia i odczytujemy różnicę wysokości słupa cieczy na manometrze, która jest proporcjonalna do nadwyżki ciśnienia p₂.

Dyskusja błędów

Powietrze jest głównie gazem dwuatomowym stąd też wynika, że dla dowolnego gazu wartość κ jest stała - zależy ona wyłącznie od budowy cząsteczek gazu. Dla gazów, których cząsteczki są dwuatomowe, a z takich w 99% składa się powietrze, κ=1,4. Nasze wyniki pomiarów wykazały odchyłkę od tej wartości . Na nieprawidłową wartość wyniku wpływ mogły wywrzeć następujące czynniki :

- nieszczelność aparatury pomiarowej mogła powodować powolne ulatnianie się sprężonego gazu z butli ( mogło dojść do wymiany ciepła z otoczeniem ), tym samym

ciśnienie gazu w butli (h2) spadało, powodując mogliśmy błędnie odczytać ustalenie się słupa cieczy w manometrze

• możliwe że zbyt krótki czas czekaliśmy na ustalenie się poziomu cieczy manometrycznej po sprężeniu i po rozprężeniu gazu. wg instrukcji powinno się odczekać kilkanaście minut,

zalecany czas otwarcia kurka jest rzędu 0,2 - 0,5 sekundy, albo za krótko albo za długo czekaliśmy na wyrównanie się ciśnienia.

Stan końcowy jest stanem po przemianach adiabatycznej oraz izochorycznej. Ten sam stan można osiągnąć drogą bezpośredniej przemiany izotermicznej, tak więc:

Wyznaczamy z równania drugiego:

i podstawiamy do pierwszego, dostajemy:

Przekształcając i rozwijając obie strony, przy założeniu p₁«p oraz p₂«p, otrzymujemy:

κ=

Ponieważ wysokość słupa cieczy w manometrze określona jest przez p_x=ρgh_x, a więc jest wprost proporcjonalna do ciśnienia, co zapisujemy:

κ=
, a Δκ_i=κ_i

Przeprowadziliśmy 6 pomiarów różnic wysokości słupa cieczy h₁ i h₂.

Wyniki i obliczenia

pomiar	h1 [mm]	h2 [mm]	h1 -h2	κ	κ ^+- Δκ
1	6,5	1,6	4,9	1,326
2	7,8	1,9	5,9	1,322
3	8,2	2	6,2	1,322	1,325 ^+- 0,9995
4	8,2	2	6,2	1,322
5	8,1	2	6,1	1,327
6	8,0	2	6,0	1,333
Wartości średnie:				1,325

Pośród otrzymanych obliczeń wykładników adiabaty  żaden wynik nie przekroczył wartości 1,4. Przyczyną tego może być nieszczelność układu doświadczalnego, co powodowało uchodzenie powietrza z butli, a tym samym wyrównywania się ciśnienia w niej panującego z atmosferycznym. Wyniki które nam wyszły nie równają się wartości kappa dla powietrza, nasze wyniki ukazują że w powietrzu zawarte są zanieczyszczenia ( bo kappa jest pomiędzy Cl a NH₃

Rodzaj gazu	gaz	
Jednoatomowy	He	1,67
	H2	1,41
	O2	1,4
dwuatomowy	N2	1,4
	Cl2	1,35
	CO2	1,3
wieloatomowe	SO2	1,29
	NH3	1,31
	C2H6	1,2

Błąd pomiarowy obliczamy ze wzoru

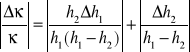
x 100%

---