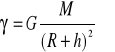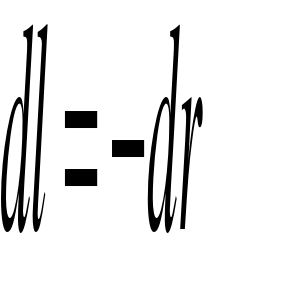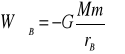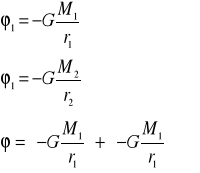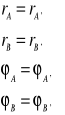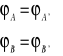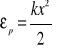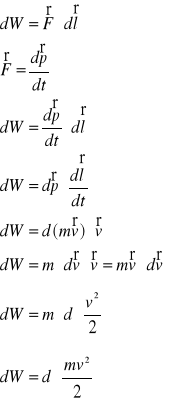Pole grawitacyjne
|
|
gdzie:
M - ciało o masie M, źródło pola
m - ciało próbne o masie m, nie deformuje pola wytworzonego przez
źródło
W otoczeniu każdego ciała przestrzeń posiada tę właściwość, że w każdym jej punkcie na ciało próbne działa siła grawitacyjna. Mówimy, że każde ciało wytwarza pole grawitacyjne.
W celu scharakteryzowania pola grawitacyjnego wprowadzamy wielkość, która nie zależy od ciała próbnego, tzw. natężenie pola grawitacyjnego.
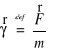
Wartość liczbowa ၧ jest równa wartości siły działającej na punkt materialny o masie m = 1 kg umieszczony w danym miejscu pola.
Kierunek ![]()
jest taki, jak kierunek siły ![]()
. W przypadku masy punktowej M (lub ciała w kształcie kuli) ![]()
ma kierunek radialny.
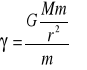
![]()
Zasada superpozycji pól
|
M1, M2 - źródła pola
Natężenie pola grawitacyjnego
|
Przy powierzchni Ziemi ၧz = 9,8 m/s2
Dla niewielkich wysokości ponad Ziemią oraz dla niewielkiego obszaru powierzchni Ziemi możemy przyjąć, że linie pola grawitacyjnego przebiegają równolegle.
|
pole jednorodne
|
W dużych odległościach od Ziemi (h duże względem R) |
|
W pobliżu Ziemi h << R |
|
Pojęcie pracy
|
|
![]()
|
|
|
Jeśli:
ၡ = 0
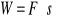
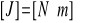
def. jednostki pracy
ၡ =
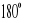
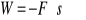
(praca ujemna)
ၡ =
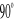
W = 0
Jeśli na ciało działają siły
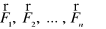
, to praca wykonana nad ciałem równa się sumie prac poszczególnych sił.
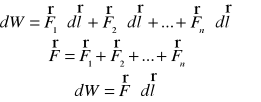
Praca siły grawitacyjnej
|
|
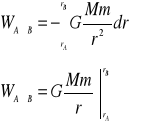
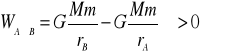
Obliczymy pracę siły zewnętrznej ![]()
przy przeniesieniu ciała z punktu
A do B.
|
przesunięcie
|
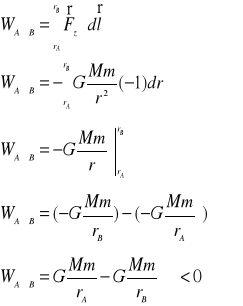
Jeśli ![]()
to
|
energia potencjalna ciała m w punkcie B pola |
Praca siły zewnętrznej przy przenoszeniu ciała m z nieskończoności do dowolnego punktu pola centralnego P wynosi:
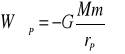
Obliczmy wartość tej pracy przy przeniesieniu masy próbnej m = 1 kg.

Tę wielkość fizyczną, która definiujemy jako stosunek pracy wykonanej przez siłę zewnętrzną ![]()
przy przeniesieniu punktu materialnego o masie m = 1 kg z nieskończoności do danego punktu P pola, nazywamy potencjałem w danym punkcie pola (lub potencjałem danego punktu pola).


prawo
gdzie:
M - masa źródła pola
rP - odległość wybranego punktu P pola od źródła pola
W przypadku np. dwóch źródeł pola M1 i M2 potencjał w punkcie P pola ![]()
|
|
Praca sił zachowawczych
|
|
|
|

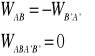
Pole grawitacyjne jest polem sił zachowawczych. Praca sił zachowawczych po krzywej zamkniętej jest równa zero.
|
|
Związek między siłą grawitacji i potencjałem grawitacyjnym
|
Siły pola są prostopadłe do powierzchni ekwipotencjalnych i zwrócone są w stronę malejącego potencjału |
![]()
Gradient potencjału (grad ϕ) jest to wektor, którego wartość jest równa szybkości wzrostu potencjału w kierunku linii sił pola.
Wartość wektora grad ϕ w tym przypadku równa się ![]()
.
|
|
|
Wartość wektora grad ϕ w tym przypadku równa się ![]()
.Praca siły ciężkości w polu jednorodnym
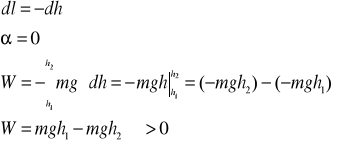
Praca równa się różnicy dwóch wyrażeń, które są funkcjami wysokości (położenia). Wyrażenie mgh nazywamy energią potencjalną ciężkości układu: Ziemia-ciało.
![]()
Potrafimy określić przyrost energii potencjalnej ciężkości
![]()
Praca wykonana przy konstrukcji układu mas punktowych o zadanej konfiguracji.
Obliczamy pracę siły zewnętrznej przy przeniesieniu masy m2 z ∞ na odległość r12 do masy m1.

Następnie obliczamy pracę przy przeniesieniu masy m3 z ∞ na odległość r13 do masy m1.

Nie uwzględniając obecności masy m1 obliczamy pracę przy przesunięciu masy m3 z ∞ na odległość r23 do masy m2.

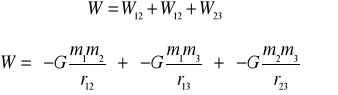
Praca siły sprężystości
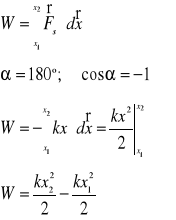
Praca W równa jest różnicy dwóch wyrażeń, które są funkcjami wychylenia ciała z położenia równowagi.
|
|
energia potencjalna sprężystości |
![]()
Praca siły F przy rozpędzaniu ciała o masie m od prędkości o wartości v1 do prędkości o wartości v2.
|
Obliczenia pomocnicze:
|
Oznaczmy wyrażenie 
.
Wyrażenie to nazwijmy energią kinetyczną ciała o masie m poruszającego się z prędkością v.
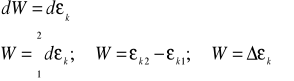
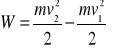
Praca W jest równa różnicy dwóch wyrażeń, które są funkcjami prędkości.
Energia jest funkcją stanu
funkcją położenia |
energia grawitacyjna |
funkcją wychylenia |
energia potencjalna sprężystości |
funkcją prędkości |
energia kinetyczna |
Zasada zachowania energii
W przypadku układu odosobnionego ![]()
suma energii potencjalnej i kinetycznej jest stała.
![]()
Pole grawitacyjne • Fizyka 2002 - 2003 |
1
|

Wyszukiwarka