1998 / 99 |
LABORATORIUM FIZYCZNE |
|||
Ćwiczenie nr 63 |
Procesy fizyczne w lampach elektronowych |
|||
ELEKTRONIKA |
ANDRZEJ KULIŚ |
|||
Wykonane dn. 07.04.99 |
|
Data |
Ocena |
Podpis |
|
T |
|
|
|
|
S |
|
|
|
1. Zasada pomiaru
Celem ćwiczenia jest zbadanie zależności natężenia prądu emisji termoelektrycznej od temperatury katody i wyznaczenie pracy wyjścia elektronu z metalu metodą prostych Richardsona.
Gęstość prądu nasycenia jn - wielkość wyrażająca prąd termoelektryczny z jednostki powierzchni katody - wzrasta ze wzrostem jej temperatury. Wartość jn wyraża wzór Richardsona - Duchmana:
![]()
(1)
jn - gęstość prądu nasycenia
T - temperatura
Ww - praca wyjścia
k - stała Boltzmana
W interesujących nas zakresach temperatur, decydujący wpływ na wartość prądu nasycenia ma wykładnik potęgowy. Logarytmując wzór (1) otrzymujemy: ![]()
(2)
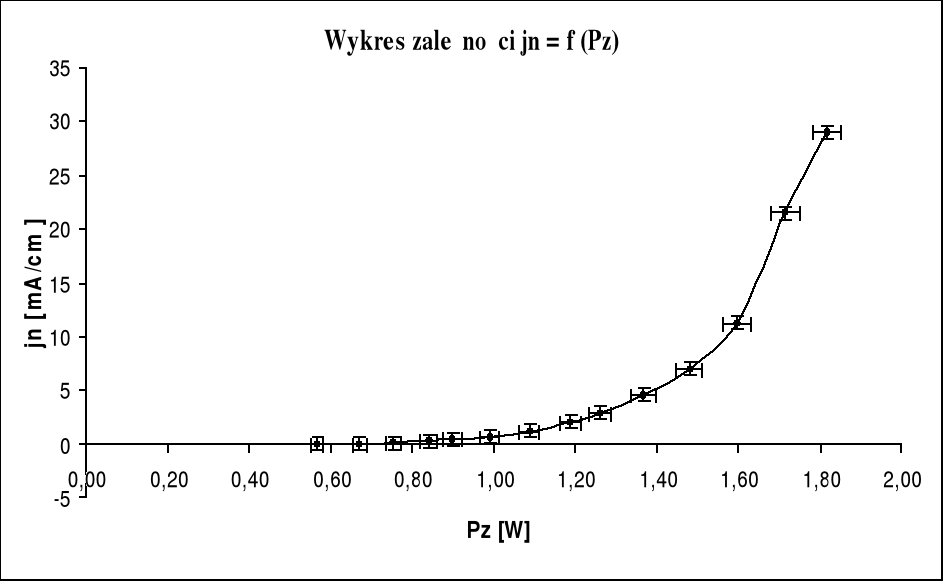
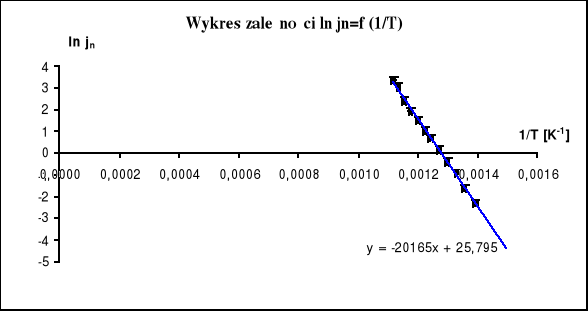
Wykresem tej zależności w układzie współrzędnych (lnjn, 1/T) jest prosta Richardsona:
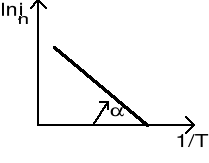
Wyrażenie ![]()
jest współczynnikiem kierunkowym prostej. Z wykresu i w oparciu o wzór (2) można więc wyznaczyć pracę wyjścia Ww:
Ww = k tg
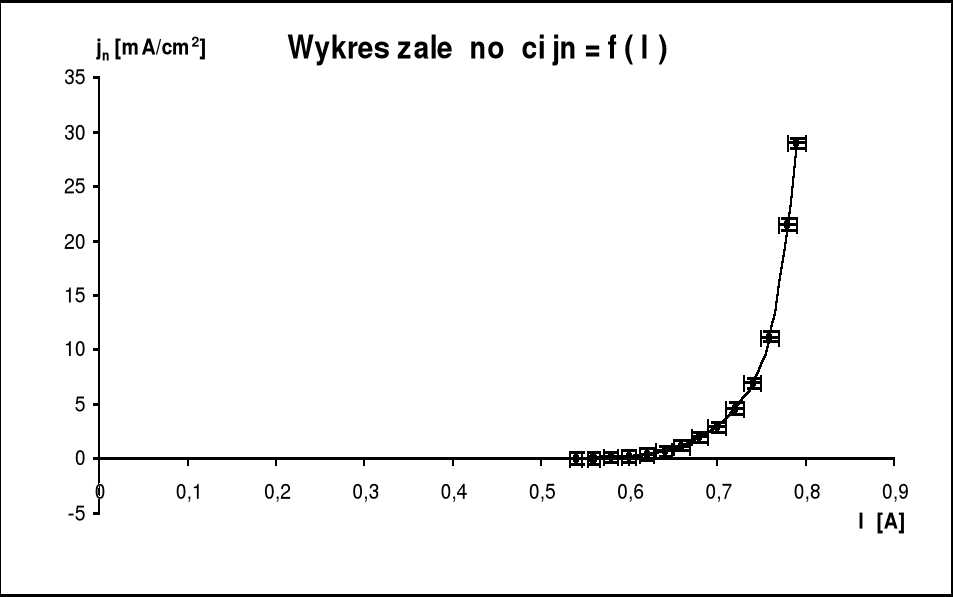
Temperaturę katody można wyznaczyć w oparciu o prawo Stefana - Boltzmana. Moc wypromieniowywana przez jednostkę powierzchni katody o temperaturze T (i jednocześnie moc żarzenia na jednostkę powierzchni katody - zużywana przez katodę na promieniowanie) wynosi:
![]()
= 5,67*10-12 W/cm2K4
= 0,5 (emisyjność całkowita lampy)
Stąd temperatura wynosi:
![]()
2. Układ pomiarowy
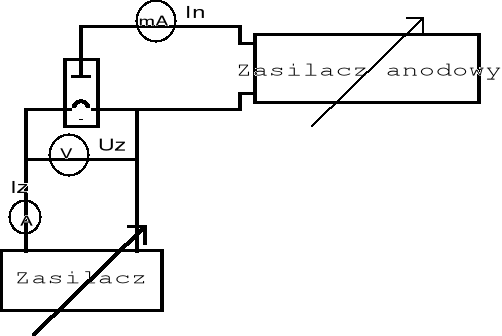
3. Ocena dokładności pojedynczych pomiarów
amperomierz (Iż) - miernik uniwersalny METEX
- zakres: 2 A
- sposób obliczania błędów pomiarowych:
1,2 % wartości wskazywanej + wartość ostatniej cyfry
miliamperomierz analogowy (In):
- ilość podziałek: 75 (zakresy: 7,5; 15)
60 (zakres 30)
- klasa dokładności: 0,5
- zakresy: 7,5 mA; 15 mA; 30 mA
woltomierz analogowy (Uż):
- ilość podziałek: 60
- klasa dokładności: 0,5
- zakres: 3 V
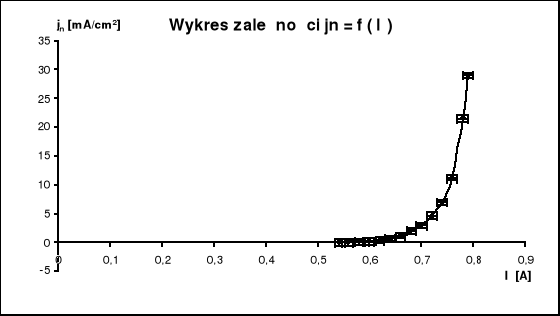
4. Wyniki pomiarów
Lp |
Ua = 150 [V] |
|||
|
Iż ± ΔIż |
Uż ± ΔUż |
In ± ΔIn |
|
|
|
|
|
zakres |
|
[A] |
[V] |
[mA] |
|
1 |
0,54 ± 0,0075 |
1,05 ± 0,015 |
0 ± 0,0375 |
7,5 |
2 |
0,56 ± 0,0077 |
1,2 ± 0,015 |
0 ± 0,0375 |
7,5 |
3 |
0,58 ± 0,0080 |
1,3 ± 0,015 |
0,1 ± 0,0375 |
7,5 |
4 |
0,6 ± 0,0082 |
1,4 ± 0,015 |
0,2 ± 0,0375 |
7,5 |
5 |
0,62 ± 0,0084 |
1,45 ± 0,015 |
0,4 ± 0,0375 |
7,5 |
6 |
0,64 ± 0,0087 |
1,55 ± 0,015 |
0,7 ± 0,0375 |
7,5 |
7 |
0,66 ± 0,0089 |
1,65 ± 0,015 |
1,2 ± 0,0375 |
7,5 |
8 |
0,68 ± 0,0092 |
1,75 ± 0,015 |
2 ± 0,0375 |
7,5 |
9 |
0,7 ± 0,0094 |
1,8 ± 0,015 |
2,9 ± 0,0375 |
7,5 |
10 |
0,72 ± 0,0096 |
1,9 ± 0,015 |
4,6 ± 0,0375 |
7,5 |
11 |
0,74 ± 0,0099 |
2 ± 0,015 |
7 ± 0,0375 |
7,5 |
12 |
0,76 ± 0,0101 |
2,1 ± 0,015 |
11,2 ± 0,075 |
15 |
13 |
0,78 ± 0,0104 |
2,2 ± 0,015 |
21,5 ± 0,15 |
30 |
14 |
0,79 ± 0,0105 |
2,3 ± 0,015 |
29 ± 0,15 |
30 |
Iż = 0,68 A
![]()
A
Iż = (0,68 0,0092) A
Uż : (zakres 3V; klasa miernika 0,5)
Uż = 1,75 V
![]()
V
Uż = (1,75 0,015 ) V
In:
(zakres 7,5 mA, klasa miernika 0,5)
In = 2 mA
![]()
mA
In = (2 0,0375 ) mA
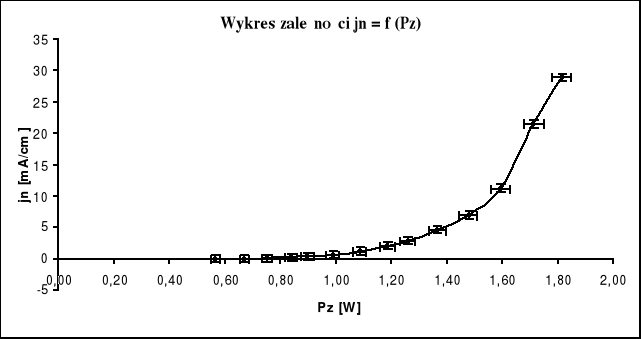
Wyniki pomiarów
Lp. |
Pż ± ΔPż |
T |
|
jn |
ln jn |
|||||
|
[W] |
[K] |
|
|
|
|||||
1 |
0,57 |
± |
0,02 |
668,74 |
0,0015 |
± |
0,0000105 |
0 |
- |
|
2 |
0,67 |
± |
0,02 |
697,76 |
0,0014 |
± |
0,0000094 |
0 |
- |
|
3 |
0,75 |
± |
0,02 |
718,13 |
0,0014 |
± |
0,0000088 |
0,1 |
-2,30 |
|
4 |
0,84 |
± |
0,02 |
737,79 |
0,0014 |
± |
0,0000083 |
0,2 |
-1,61 |
|
5 |
0,90 |
± |
0,02 |
750,42 |
0,0013 |
± |
0,0000080 |
0,4 |
-0,92 |
|
6 |
0,99 |
± |
0,02 |
769,11 |
0,0013 |
± |
0,0000076 |
0,7 |
-0,36 |
|
7 |
1,09 |
± |
0,02 |
787,26 |
0,0013 |
± |
0,0000072 |
1,2 |
0,18 |
|
8 |
1,19 |
± |
0,03 |
804,91 |
0,0012 |
± |
0,0000068 |
2 |
0,69 |
|
9 |
1,26 |
± |
0,03 |
816,50 |
0,0012 |
± |
0,0000067 |
2,9 |
1,06 |
|
10 |
1,37 |
± |
0,03 |
833,46 |
0,0012 |
± |
0,0000064 |
4,6 |
1,53 |
|
11 |
1,48 |
± |
0,03 |
850,02 |
0,0012 |
± |
0,0000061 |
7 |
1,95 |
|
12 |
1,60 |
± |
0,03 |
866,20 |
0,0012 |
± |
0,0000059 |
11,2 |
2,42 |
|
13 |
1,72 |
± |
0,03 |
882,05 |
0,0011 |
± |
0,0000057 |
21,5 |
3,07 |
|
14 |
1,82 |
± |
0,04 |
894,75 |
0,0011 |
± |
0,0000055 |
29 |
3,37 |
|
![]()
Sk=1 cm2
![]()
![]()
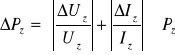
=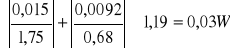
![]()
Pż= (1,19 0,03) W
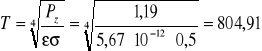
![]()
1/T = 0,0012 ![]()
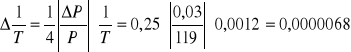
![]()
![]()
= (0,0012 0,0000068) ![]()
![]()
= ![]()
![]()
5. Dyskusja błędów
Błędy zastosowanych przyrządów pomiarowych podane są w punktcie 3. Błędy wielkości złożonych zostały obliczone metodą różniczki logarytmicznej, gdyż wszystkie one są wielkościami iloczynowymi:
![]()
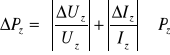
![]()
( i - stałe) 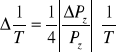
![]()
(Sk - stała) 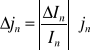
lnjn=(In/In)*lnjn
Błędy Δjn są równe wartościowo błędom ΔIn .
6. Obliczenie pracy wyjścia
Korzystając z obliczonego na podstawie wykresu ln jn=f![]()
tangensa kąta prostej, można korzystając ze wzoru W = k ⋅ tg
obliczyć pracę wyjścia elektronów:
k = 1,380662*10-23 J/K
1J = 6,242*1018eV
![]()
![]()
W =20627,73*1,380662*10-23 = 2,8479922*10-19 J = 1,777 eV
7. Zestawienie wyników
Wynik jest porównywalny z wartościami pracy wyjścia różnych metali, podawanymi w tabelach - od 1,8 eV dla litu do 4,7 eV dla srebra. W tabelach nie znalazłem pierwiastka o dokładnie takiej samej pracy wyjścia.
Praca wyjścia elektronu z katody badanej lampy wynosi:
Ww = 1,777 eV
8. Uwagi i wnioski
Zjawisko emisji termoelektronowej polega na wysyłaniu elektronów przez nagrzane metale. Elektron przewodzenia może opuścić dany metal jedynie wówczas, gdy jego energia W przewyższa pracę wyjścia elektronu z metalu. Gęstość elektronów swobodnych w metalu jest bardzo duża; ich prędkości cieplne w danej temperaturze są różne i złożone. Oznacza to, że nawet w średnich temperaturach występuje w metalu dostatecznie duża liczba elektronów przewodzenia, zdolnych wykonać pracę wyjścia i opuścić metal. W temperaturze metalu rzędu kilkuset stopni skali bezwzględnej zjawisko emisji termoelektronowej staje się bardzo intensywne. W wyniku emisji termoelektronowej powstaje prąd termoelektronowy, którego natężenie zależy od napięcia wytworzonego między elektrodami, od temperatury katody oraz od materiału z jakiego jest ona wykonana. Maksymalny prąd termoelektronowy powstający przy danej temperaturze katody nazywamy prądem nasycenia In. Prąd ten rośnie w miarę podwyższania temperatury katody.
2 MARCHEWKA. Opracowanie doświadczenia 1998 / 99.
Wyszukiwarka