Zasada Tellegena

W każdym obwodzie moc chwilowa pobierana przez cały obwód, równa sumie mocy pobieranych przez wszystkie gałęzie, w każdej chwili jest równa zeru.

Moc chwilowa pobierana przez k-tą gałąź jest równa p_k = u_ki_k, więc moc chwilowa pobierana przez cały obwód o b gałęziach wyraża się następująco

gdzie u, i - wektory napięć i prądów gałęziowych są b-elementowymi macierzami kolumnowymi, a T oznacza transpozycję macierzy.

Korzystając z powyższego równania zasadę Tellegena wyrażamy następująco

lub

Można wykazać, że zasada Tellegena jest konsekwencją obu praw Kirchhoffa. Oznacza to, że ze spełnienia obu praw Kirchhoffa wynika spełnienie zasady Tellegena.

Zasada Tellegena obowiązuje zarówno w obwodach liniowych jak i nieliniowych.

Elementy topologii obwodów

1. Wstęp

Topologia obwodów zajmuje się tymi właściwościami obwodów skupionych, które dotyczą struktury połączeń poszczególnych elementów obwodu. Elementarnymi pojęciami stosowanymi w topologii obwodów są: węzeł i gałąź.

Węzłem nazywamy punkt połączenia dwóch lub większej liczby elementów obwodu. Wielkością elektryczną, która związana jest z węzłem, jest jego potencjał względem węzła odniesienia o potencjale równym zero.

Gałęzią nazywamy jeden lub kilka elementów włączonych między dwoma węzłami. Wielkościami elektrycznymi związanymi z gałęzią są prąd i napięcie gałęzi równe różnicy potencjałów węzłów, między którymi włączona jest gałąź.

Gałąź dołączoną do węzła nazywamy gałęzią incydentną z tym węzłem.

2. Graf i pojęcia z nim związane

Grafem G obwodu nazywamy odwzorowanie, które każdej gałęzi b_i ∈ B przyporządkowuje jednoznacznie parę n_i, n_j ∈ N; gdzie: B - zbiór gałęzi rozpatrywanego obwodu, N - zbiór węzłów tego obwodu.

Rys. 2.1. Przykład obwodu o 6 gałęziach i czterech węzłach a) obwód b) graf

Graf obwodu z rys. 2.1a można zdefiniować następująco

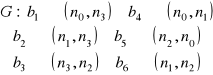
Obwodowi z oznaczonymi zwrotami prądów w gałęziach przyporządkowuje się graf skierowany, który można przedstawić w postaci rysunku (rys. 2.1b), gdzie każdą gałąź obwodu zastępujemy odcinkiem linii ze strzałką, o takim zwrocie jak zwrot prądu. Taki odcinek nazywamy krawędzią lub gałęzią grafu. Węzłom obwodu przyporządkowuje się punkty o tych samych numerach co numery węzłów obwodu. Punkty te nazywamy wierzchołkami lub węzłami grafu.

Ścieżka

Ciąg gałęzi nazywamy ścieżką łączącą węzły n_j, n_k, jeśli:

• kolejne gałęzie mają jedną wspólną końcówkę,

• żaden węzeł nie stanowi końcówki więcej niż dwóch gałęzi ciągu.

Inaczej mówiąc, ścieżka jest drogą pomiędzy dwoma węzłami, nie tworząca linii zamkniętej.

Graf spójny

Graf nazywamy spójnym, jeśli istnieje ścieżka między każdymi dwoma węzłami grafu. Graf, który nie jest spójny nazywamy rozłącznym.

Oczko (kontur)

Oczkiem nazywamy spójny podgraf, w którym każdy węzeł stanowi końcówkę dokładnie dwóch gałęzi. Oczku nadaje się zwrot zgodny lub przeciwny do ruchu wskazówek zegara. Oczko z zaznaczonym zwrotem nazywamy oczkiem zorientowanym.

Drzewo

Drzewem nazywamy podgraf, który jest:

• spójny,

• zawiera wszystkie węzły grafu,

• nie zawiera oczek.

Przykłady drzew grafu z rys. 2.1b pokazano na rys. 2.2.

Rys. 2.2. Przykłady drzew obwodu z rys. 2.1b

Gałęzie nie należące do drzewa nazywamy cięciwami. Dla grafu spójnego o n węzłach każde drzewo ma dokładnie n-1 gałęzi. Jeżeli z grafu wybierze się n-1 gałęzi, tak aby nie tworzyły oczka, to gałęzie te stanowić będą drzewo.

Rozcięcie (przekrój)

Zbiór gałęzi grafu spójnego nazywamy rozcięciem, jeśli:

• usunięcie z grafu tego zbioru gałęzi (bez końcówek) powoduje, że graf staje się niespójny,

• powrót jakiejkolwiek jednej gałęzi zbioru do grafu powoduje, że staje się on ponownie spójny.

Rys. 2.3. Przykłady rozcięć

3. Macierze strukturalne

Macierz węzłowa (macierz incydencji)

Informacje zawarte w grafie skierowanym można w pełni zapisać za pomocą macierzy węzłowej. Pełną macierzą węzłową A_a obwodu o n węzłach i b gałęziach jest macierz o n wierszach i b kolumnach, gdzie:

• a_ij=1, jeśli i-ty węzeł jest końcem j-tej gałęzi (strzałka skierowana od węzła i-tego),

• a_ij=-1, jeśli i-ty węzeł jest początkiem j-tej gałęzi (strzałka skierowana do i-tego węzła),

• a_ij=0, jeśli j-ta gałąź nie jest incydentna z i-tym węzłem.

Rys. 3.1. Graf z zaznaczonymi węzłami

Dla grafu z rys. 3.1 mamy

Każda kolumna pełnej macierzy węzłowej ma dokładnie dwa elementy różne od zera. Bez zmniejszenia ilości zawartych informacji możemy z takiej macierzy wykreślić dowolny wiersz. Wiersz taki można zawsze odtworzyć, korzystając z własności, że suma elementów każdej kolumny pełnej macierzy węzłowej jest równa zeru.

Macierz otrzymaną przez wykreślenie z pełnej macierzy węzłowej A_a dowolnego wiersza nazywamy macierzą węzłową (macierzą incydencji) A. Węzeł odpowiadający skreślonemu węzłowi nazywamy węzłem odniesienia. Pozostały zbiór węzłów nazywamy układem węzłów niezależnych.

Macierz węzłowa ma następujące właściwości:

• wiersze macierzy węzłowej A są liniowo niezależne,

• jeśli A jest macierzą węzłową grafu spójnego mającego n węzłów, to n - 1 kolumn macierzy A jest liniowo niezależnych wtedy i tylko wtedy, gdy gałęzie odpowiadające tym kolumnom tworzą drzewo grafu.

Wynika stąd, że jeśli macierz A zostanie podzielona następująco

gdzie kolumny macierzy A_T odpowiadają gałęziom drzewa, a kolumny macierzy A_L odpowiadają cięciwom, to

Przykładowo, jeżeli dla grafu z rys. 3.1 jako drzewo wybierzemy gałęzie (4, 5, 6) i jako węzeł odniesienia wybierzemy węzeł (0), to otrzymamy

Macierz rozcięć

Pełną macierzą rozcięć D_a grafu skierowanego mającego n_c zorientowanych (z zaznaczonymi zwrotami) rozcięć oraz b gałęzi jest macierz o n_c wierszach i b kolumnach, gdzie:

• d_ij=1, jeśli gałąź j należy do rozcięcia i oraz ma ten sam zwrot co rozcięcie,

• d_ij=-1, jeśli gałąź j należy do rozcięcia i oraz ma przeciwny zwrot niż rozcięcie,

• d_ij=0, jeśli gałąź j nie należy do rozcięcia i.

Rys. 3.2. Graf z oznaczonymi rozcięciami

Graf z rys. 3.2 ma sześć rozcięć, a odpowiadająca mu pełna macierz rozcięć ma postać

Po wykreśleniu z pełnej macierzy D_a takiej minimalnej liczby wierszy, aby pozostałe wiersze były liniowo niezależne, otrzymuje się macierz rozcięć D.

Dla grafu spójnego o n węzłach macierz rozcięć D ma (n - 1) wierszy. Każdy zbiór rozcięć, którym odpowiadają liniowo niezależne wiersze macierzy D_a, nazywamy układem rozcięć niezależnych.

Macierz rozcięć otrzymuje się korzystając z drzewa obwodu i stosując następujące zasady:

• każda gałąź drzewa razem z pewną liczbą cięciw tworzy rozcięcie,

• zwrot rozcięcia przyjmuje się zgodny z ze zwrotem odpowiadającej mu gałęzi drzewa.

Tak wybrane rozcięcia nazywamy rozcięciami fundamentalnymi. Graf spójny mający n węzłów ma n - 1 gałęzi drzewa, a zatem również n - 1 rozcięć fundamentalnych.

Jeżeli dla grafu z rys. 3.2 drzewo zostanie utworzone z gałęzi (1, 3, 4) to macierz rozcięć będzie następująca

Nie wszystkie możliwe zbiory rozcięć niezależnych mogą być utworzone na podstawie odpowiadającego im drzewa. Na przykład zbiorowi rozcięć niezależnych (1, 2, 3) nie odpowiada żadne drzewo.

Macierz D może być podzielona następująco

gdzie kolumny macierzy jednostkowej I odpowiadają gałęziom drzewa, a kolumny macierzy D_L odpowiadają cięciwom.

Macierz oczkowa

Pełną macierz oczkową B_a grafu skierowanego o b gałęziach i n_l zorientowanych oczkach jest macierz o n_l wierszach i b kolumnach, w gdzie:

• a_ij=1, jeśli gałąź j należy do oczka i oraz ma ten sam zwrot co oczko,

• a_ij=-1, jeśli gałąź j należy do oczka i, a ma przeciwny zwrot niż oczko,

• a_ij=0, jeśli gałąź j nie należy do oczka i.

Rys. 3.3. Graf z oznaczonymi oczkami

Pełna macierz oczkowa grafu z rys. 3.3 ma postać

Wiersze macierzy oczkowej nie są liniowo niezależne. Po wykreśleniu z pełnej macierzy oczkowej B_a takiej minimalnej liczby wierszy, aby pozostałe wiersze były liniowo niezależne, otrzymuje się macierz oczkową B.

Dla grafu spójnego mającego b gałęzi i n węzłów macierz oczkowa B ma b - n + 1 wierszy. Każdy zbiór oczek, którym odpowiadają liniowo niezależne wiersze macierzy B_a nazywa się układem oczek niezależnych.

Macierz oczkową otrzymuje się korzystając z drzewa obwodu i stosując następujące zasady:

• każda cięciwa razem z jedną i tylko jedną ścieżką drzewa tworzy oczko,

• zwrot oczka przyjmuje się zgodnie ze zwrotem cięciwy.

Tak wybrane oczka nazywane są oczkami fundamentalnymi. Graf spójny mający n węzłów i b gałęzi ma b - n + 1 cięciw, a zatem również b - n + 1 oczek fundamentalnych.

Jeśli dla grafu z rys. 3.3 wybierzemy drzewo utworzone z gałęzi (1, 4) to macierz oczkowa odpowiadająca temu drzewu będzie następująca

Nie wszystkie możliwe zbiory oczek niezależnych mogą być utworzone na podstawie odpowiadającego im drzewa. Na przykład zbiorowi oczek niezależnych (1, 2, 3) nie odpowiada żadne drzewo.

Zbiór oczek niezależnych można wybrać nie korzystając z drzewa. Pierwsze oczko wybieramy dowolnie. Kolejne wybierane oczko musi zawierać przynajmniej jedną gałąź nie należącą do oczek wybranych wcześniej. Tak należy wybrać b - n + 1 oczek.

Macierz B wygenerowana na podstawie drzewa może być podzielona następująco

gdzie kolumny macierzy B_T odpowiadają gałęziom drzewa, a kolumny macierzy jednostkowej I, stopnia b - n + 1, odpowiadają cięciwom.

Iloczyn macierzy oczkowej i węzłowej jest równy macierzy zerowej

przy czym indeks górny T oznacza transpozycję macierzy. Oznacza to, że macierze te są ortogonalne. Jeśli w powyższym równaniu macierze węzłową i oczkową zastąpimy pełnymi macierzami: węzłową i oczkową, to równanie również będzie prawdziwe. Podobnie, jeśli macierz węzłowa A zostanie zastąpiona macierzą rozcięć D.

4. Prawa Kirchhoffa

Prądowe prawo Kirchhoffa

Suma prądów wszystkich gałęzi incydentnych z węzłem obwodu jest w każdej chwili równa zeru.

Rys. 4.1. Przykład prądowego prawa Kirchhoffa dla węzła

Przykładowo, dla węzła W z rys. 4.1 mamy

Prądowe prawo Kirchhoffa można sformułować również w odniesieniu do rozcięć. Suma prądów wszystkich gałęzi należących do rozcięcia jest w każdej chwili równa zeru.

Rys. 4.2. Przykład prądowego prawa Kirchhoffa dla rozcięcia

Przykładowo, dla obwodu z rys. 4.2 mamy

Prądowe prawo Kirchhoffa można wyrazić, korzystając ze strukturalnej macierzy węzłowej (incydencji) lub strukturalnej macierzy rozcięć. Oznaczmy wektory (macierze kolumnowe) prądów gałęziowych oraz napięć gałęziowych obwodu o b gałęziach

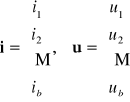
Przy tak oznaczonym wektorze prądów gałęziowych prądowe prawo Kirchhoffa można wyrazić następująco:

• dla węzłów: A_ai = 0

• dla rozcięć: D_ai = 0

Powyższe równania, w których występują pełne macierze, odpowiednio, węzłowa i rozcięć, nie tworzą układów równań liniowo niezależnych. Układy te są nadmiarowe. Równania te są spełnione wtedy i tylko wtedy, gdy

(4.1)

Oznacza to, że prądowe prawo Kirchhoffa jest spełnione dla wszystkich węzłów i wszystkich rozcięć wtedy i tylko wtedy, gdy spełnione jest dla węzłów niezależnych lub rozcięć niezależnych.

Napięciowe prawo Kirchhoffa

Suma napięć wszystkich gałęzi należących do oczka jest w każdej chwili równa zeru.

Rys. 4.3. Przykład napięciowego prawa Kirchhoffa

Przykładowo, dla oczka pokazanego na rys. 4.3, zawierającego cztery gałęzie, równanie wynikające z napięciowego prawa Kirchhoffa można napisać w następujący sposób. Obieramy jako dodatni zwrot zgodny z ruchem wskazówek zegara (można wybrać zwrot przeciwny), tak jak pokazano na rysunku. Jeżeli napięcia, których zwroty są zgodne z zaznaczonym zwrotem, zapiszemy ze znakiem plus, a napięcia, których zwroty są przeciwne do obranego kierunku, ze znakiem minus, to tak zapisana suma jest równa zeru.

Napięciowe prawo Kirchhoffa można wyrazić, korzystając ze strukturalnej macierzy oczkowej

Powyższe równanie macierzowe, w którym występuje pełna macierz oczkowa, nie tworzy układu równań liniowo niezależnych. Układ ten jest nadmiarowy. Równanie to jest spełnione wtedy i tylko wtedy, gdy

(4.2)

Oznacza to, że napięciowe prawo Kirchhoffa jest spełnione dla wszystkich oczek wtedy i tylko wtedy, gdy spełnione jest dla oczek niezależnych. Równania (4.1) i (4.2) noszą nazwę równań równowagi.

5. Potencjały węzłowe i prądy oczkowe

Potencjały węzłowe

Potencjałem węzłowym węzła W nazywamy napięcie między tym węzłem a węzłem odniesienia. Jako węzeł odniesienia może być wybrany dowolny węzeł.

Niech węzłem odniesienia w obwodzie z rys. 5.1 będzie węzeł (0). Jak pokazano na rysunku, potencjałami węzłowymi są napięcia v₁, v₂, v₃, równe napięciom między poszczególnymi węzłami a węzłem (0).

Rys. 5.1. Obwód z oznaczonymi potencjałami węzłowymi i prądami oczkowymi

W rozpatrywanym przykładzie liczba potencjałów węzłowych jest równa 3. Ogólnie liczba potencjałów węzłowych obwodu o n węzłach jest równa n - 1. Napięcia gałęziowe można wyrazić przez potencjały węzłowe, na przykład dla obwodu z rys. 5.1 mamy

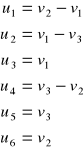
Ogólnie zależność między potencjałami węzłowymi a napięciami gałęziowymi określa równanie

(5.1)

w którym

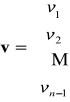
wektor potencjałów węzłowych, u wektor napięć gałęziowych oraz A^T transponowana macierz węzłowa.

Można udowodnić, że istnienie wektora potencjałów węzłowych v spełniającego równanie (5.1) jest równoważne spełnieniu napięciowego prawa Kirchhoffa. Oznacza to, że równania równowagi można wyrazić, posługując się tylko macierzą strukturalną węzłową. W tym ujęciu równania równowagi mają postać

Prądy oczkowe

Prądem oczkowym nazywamy prąd, który zatacza w oczku jeden cykl, płynąc przez wszystkie gałęzie oczka. W obwodzie o b gałęziach i n węzłach, prądy b - n + 1 oczek niezależnych tworzą układ zmiennych niezależnych.

Trzy prądy oczkowe i_o1, i_o2, i_o3 oznaczone na rys. 5.1 tworzą układ zmiennych niezależnych. Prądy gałęziowe można wyrazić przez prądy oczkowe, a mianowicie

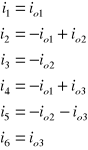
Ogólnie zależność między prądami oczkowymi a prądami gałęziowymi określa równanie

(5.2)

w którym

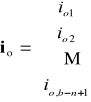
wektor prądów oczkowych, i - wektor prądów gałęziowych oraz B^T transponowana macierz oczkowa.

Można udowodnić, że istnienie wektora prądów oczkowych i_o spełniającego równanie (5.2) jest równoważne spełnieniu prądowego prawa Kirchhoffa. Oznacza to, że równania równowagi można wyrazić, posługując się tylko macierzą strukturalną oczkową. W tym ujęciu równania równowagi mają postać

---