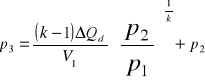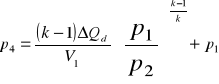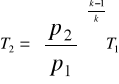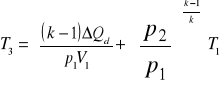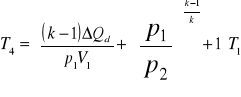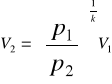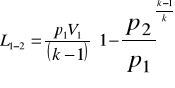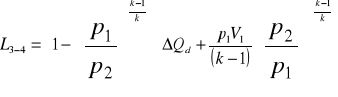Zad.II 4.2 Piotr Bibik M 3.1
Parametry stanu w punktach charakterystycznych obiegu Otto są odpowiednio równe: przed zgęszczaniem adiabatycznym ciśnienie ![]()
, temperatura ![]()
, zasób objętości
![]()
zaś po zagęszczeniu adiabatycznym ciśnienie![]()
, temperatura 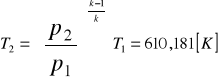
, zasób objętości 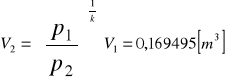
. Po przemianie izochorycznego sprężania ciśnienie 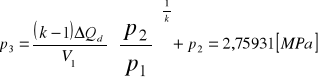
, temperatura 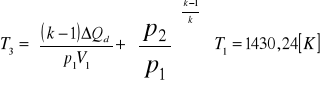
, zasób objętości ![]()
. Po przemianie adiabatycznego rozgęszczania ciśnienie 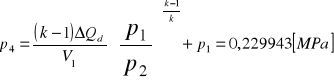
,
temperatura 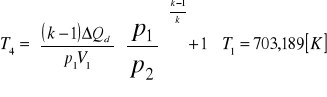
zaś zasób objętości ![]()
.
Podczas przemiany izochorycznego sprężania do obiegu doprowadzono przyrost ilości ciepła ![]()
. Zakładamy, że przemiany obiegu są przemianami odwracalnymi oraz, że czynnikiem pracującym w obiegu jest powietrze traktowane tak jak gaz doskonały dla którego indywidualna stała gazowa 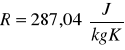
zaś wykładnik izentropy k=1,4. Obliczyć prace bezwzględne objętościowe przemian obiegu Otto.
Rozwiązanie:
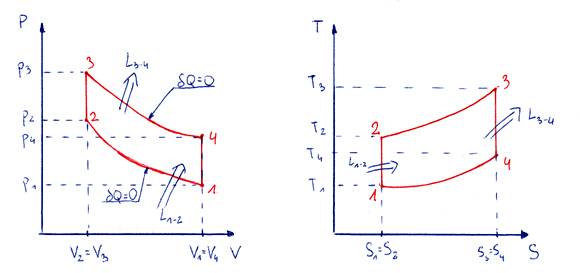
Wykresy obiegu termodynamicznego Otto dla powietrza we współrzędnych PV i TS z zaznaczonymi przepływami pracy bezwzględnej objętościowej:
2. Tabela zestawienia danych i wyników obliczeń
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
3.Obliczam pracę bezwzględną objętościową obiegu Otto
3.1 Obliczam pracę bezwzględną objętościową przemiany izotropowej między punktami 1 i 2.
Pierwsza postać I zasady termodynamiki
![]()
![]()
dla przemiany izotropowej:
![]()
![]()
Zasób energii wewnętrznej określony jest związkiem:
![]()
gaz doskonały ![]()
układ substancjalny m=const
![]()
![]()
całkując w granicach
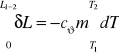
![]()
Z równania Mayera i definicji wykładnika izentropy:
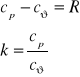
otrzymujemy
![]()
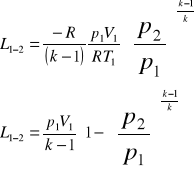
3.2 Obliczam pracę bezwzględną objętościową przemiany izotropowej między punktami 3 i 4 obiegu
![]()
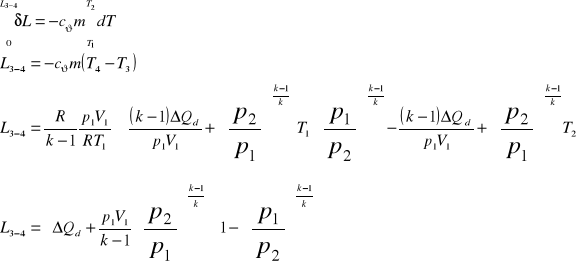
3.3 Obliczam wartość pracy bezwzględnej objętościowej przemiany izotropowej między punktami 1-2 oraz 3-4
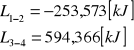
Wyszukiwarka