17. Prawo Newtona, jednostki

Prawo newtona: Siła F wprowadzająca ciecz w ruch jest proporcjonalna do powierzchni S poruszających się względem siebie warstw cieczy oraz do spadku prędkości ∆V/∆x czyli:

F=Sη (∆V/∆x)

η - współczynnik lepkości (lepkość)

Jednostki lepkości: [η]=Ns/m²= kg/ms

Jednostka spoza układu Si: zwana Puazem ( P) 1P=10 ¹̄ Ns/m²

18. Reologia, wielkości, definicje

Reologia- obejmuje zagadnienia dotyczące odkształcenia i przepływu materii- czyli ruchu jednych elementów ośrodka względem innych. Przepływ cieczy lepkiej jest jednym ze specjalnych przypadków odkształcenia postaci materii.

Oddziaływania występujące w przepływających płynach można charakteryzować podając naprężenia styczne: τ = F/S , jako funkcję prędkości ścinania (u=dv/dx).

Wykres τ=f(u) nazywamy krzywą płynięcia. Różnicuje ona płyny na dwie kategorie: newtonowskie i nienewtonowskie. Dla pierwszej kategorii wykresem jest linia prosta przechodząca przez początek układu współrzędnych dla drugiej kategorii linia nie przechodzi przez początek.

Iloraz : τ/u jest lepkością płynu (η)

Rodzaje lepkości:

Lepkość względna i jej definicja: [η̕]=η/η₀

Lepkość właściwa Definicja: η_wł= (η/η₀)-1

Lepkość graniczna Definicja:

L. względna i właściwa- bezwymiarowe wielkości

L. graniczna- oznacza ηwł/c przy stężeniu c oraz u zmierzających do 0. Wyznaczamy ją z granicznej zależności: η_wł/c=[η] + k[η] gdzie k- stała Huggina

19. Ciecze newtonowskie i nienewtonowskie, podziały

Dla płynów newtonowskich lepkość nie zależy od szybkości ścinania, zależy natomiast od własności substancji tworzącej płyn i jego parametrów termodynamicznych takich jak temperatura i ciśnienie. Istnieją płyny, zwane płynami nienewtonowskimi, które nie spełniają powyższej zależności, dla nich naprężenia nie są proporcjonalne do gradientu prędkości, co jest równoznaczne z tym, że współczynnik lepkości nie jest stały lecz jest funkcją gradientu prędkości. Zależność naprężeń od gradientu prędkości przedstawiona na wykresie nosi nazwę krzywej płynięcia. Dla płynu newtonowskiego krzywa płynięcia jest prostą przechodzącą przez początku układu współrzędnych.

Krzywa płynięcia dla płynu newtonowskiego

Jeżeli krzywa płynięcia jakiegoś płynu nie jest prostą przechodzącą przez początek układu współrzędnych płyn taki jest płynem nienewtonowskim, lecz płynem z granicą płynięcia. Płyn newtonowski można też traktować jako specjalny przypadek płynu nienewtonowskiego.

20. Ciecze tiksotropowe

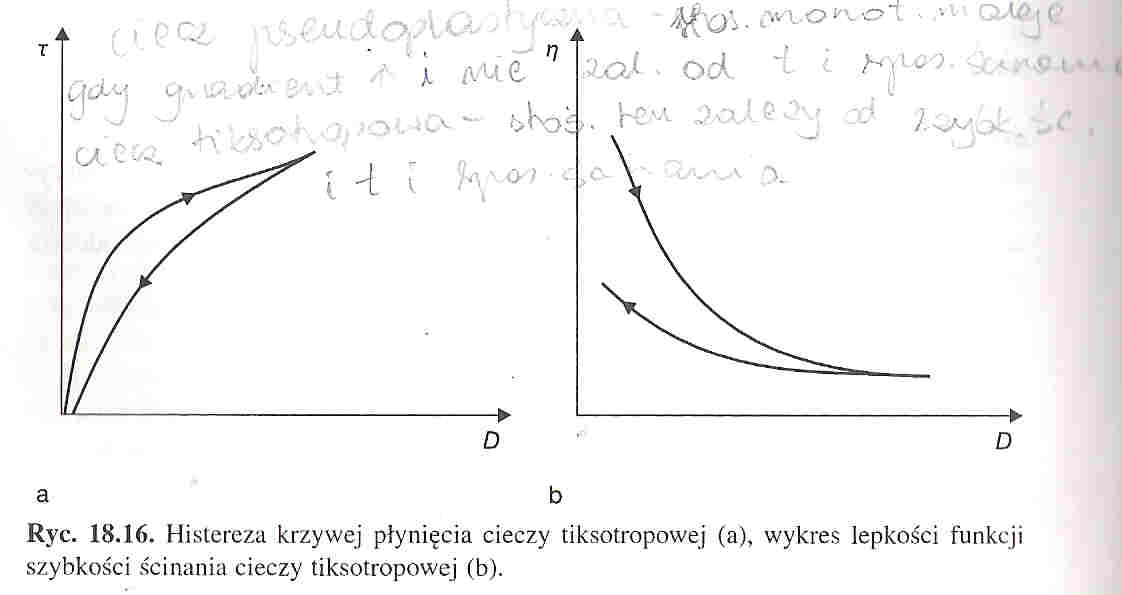
W cieczach tiksotropowych stosunek naprężenia ścinającego do gradientu prędkości zależy od szybkości, czasu i sposobu ścinania. Dla cieczy tiksotropowej krzywa płynięcia(wykres zależności naprężenia ścinającego od szybkości ścinania) wykazuje histerezę. Właściwości tiksotropowe krwi są związane z tworzeniem struktur w warunkach braku ścinania oraz i rozpadaniem się w obecności naprężeń ścinających. Dzięki temu badania krzywych płynięcia i ich analiza pozwalają wyciągnąć wnioski na temat rozmiarów struktur, łatwości ich tworzenia i warunków w jakich ulegają rozpadowi. Właściwości tiksotropowe krwi związane są z tworzeniem i rozpadaniem skupisk krwinek czerwonych. Zjawisko to nazywa się agregacją krwinek czerwonych. Odtwarzanie struktur odbywa się w bardzo krótkim czasie, w związku z tym histereza krzywej płynięcia jest prawie niezauważalna.

21. Ciecze pseudoplastyczne

Cieczami pseudoplastycznymi nazywa się ciecze w których stosunek naprężenia ścinającego do gradientu prędkości w określonych warunkach temperatury i ciśnienia nie jest stały. Może on także monotonicznie maleć wraz ze wzrostem gradientu prędkości lecz nie zależeć od czasu i sposobu ścinania. Taką ciecz jest między innymi krew.

22. Wzór Einsteina na lepkość

Wzór Einsteina określa lepkość względną roztworu, w Którym cząsteczki substancji rozpuszczonej mają kształt kulisty.

Gdzie:

Φ=
- współczynnik objętościowy roztworu; Vc-objętość cząsteczek substancji rozpuszczonej, Vr- objętość całkowita roztworu

η lepkość roztworu

η.-lepkość rozpuszczalnika

Objętość cząsteczek substancji rozpuszczonej jest równa iloczynowi liczby n moli tej substancji, liczby Avogadra N_A i objętości V jednej cząsteczki:

Φ

Jeżeli uwzględnimy że M=
zaś c=
to powyższy wzór będzie wyglądał:

Φ

23. Akumulacja osiowa, efekt Magnusa

- Akumulacja osiowa polega na tym, że krwinki gromadzą się bliżej osi naczynia unikając jego ścian.

- Powstawanie akumulacji osiowej tłumaczy się efektem Magnusa (na ciało wykonujące ruch obrotowy i poruszające się ruchem postępowym działa siła prostopadła do tego ruchu powodująca odchylenie).

- Ruch obrotowy wywołujący efekt Magnusa (a co za tym idzie akumulację krwinek) powstaje w skutek wytworzonego gradientu prędkości (powstaję on ze względu na to, że bliżej ścianek naczynia warstwy płynu poruszają się wolniej). Ruch obrotowy pociąga za sobą ciecz nadając jej ruch cyrkulacyjny wokół krwinki, co jest powodem rozrzedzenia linii prądu przy odściennej stronie krwinki a zagęszczenie ich od strony odosiowej. W ten sposób wytwarza się różnica ciśnień, która znosi krwinkę do osi przewodu.

- Akumulacją osiową krwinek tłumaczy się zależność lepkości krwi od prędkości przepływu.

- W warunkach fizjologicznych krew zachowuje się jak ciecz newtonowska i lepkość prawię nie zależy od prędkości przepływu, jednakże akumulacja osiowa powoduje, że lepkość jest mniejsza (warstwa cieczy między ścianą a strumieniem krwinek zmniejsza tarcie)

24. Przepływ laminarny

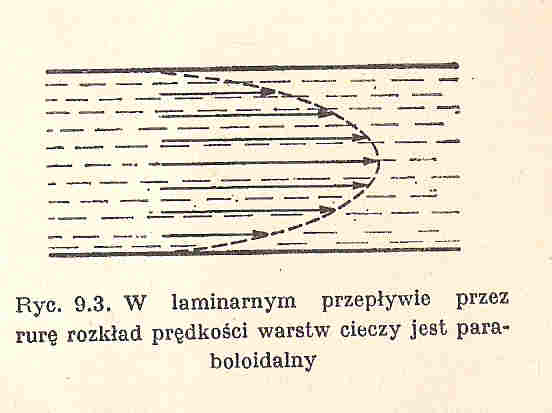
Przepływ laminarny (warstwowy) - jest to taki rodzaj przepływu płynu lepkiego, w którym największą prędkość ma ciecz poruszająca się wzdłuż osi przewodu, a ciecz przy ściance pozostaje nieruchoma (występuje gradient prędkości wywołany tarciem wewnętrznym <<lepkością>>). Zachodzi dla małych prędkości przepływu, gdy liczba Reynoldsa nie przekracza tzw. wartości krytycznej (powyżej której przepływ staje się turbulentny).

Objętość V cieczy przepływającej laminarnie w czasie t przez poprzeczny przekrój rurki włoskowatej o promieniu r i długości l, na końcach której panuje różnica ciśnień Δp jest określana prawem Poiseuille'a (które wykorzystujemy w pomiarze współczynnika lepkości).

25. Budowa lampy rentgenowskiej i 26. Wytwarzanie promieni rentgenowskich

Działanie lampy rentgenowskiej opiera się na wykorzystaniu elektronów o wysokich energiach kinetycznych zaś uzyskanie promieniowania rentgenowskiego jest możliwe dzięki hamowaniu tych elektronów na anodzie lampy rentgenowskiej.

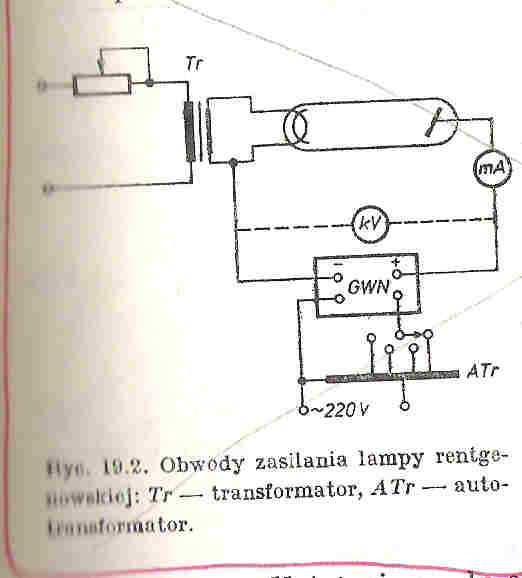
Lampa rentgenowska zbudowana jest z Katody (umieszczonej w czaszy ogniskującej) najczęściej wolframowej na, której na wskutek przyłożonego napięcia (ok. 10V) na drodze termoemisji wytwarzane są elektrony. Ilość emitowanych elektronów może być regulowana za pomocą umieszczonego w obwodzie katodowym opornika zmiennego, którym można regulować rozżarzenie katody.

Elektrony uzyskują wysoką energię kinetyczną w silnym polu elektrycznym, które powstaje dzięki przyłożonemu napięciu (od kilku do kilkuset tysięcy Volt), uzyskiwane dzięki generatorowi wysokich napięć (GWN), a następnie są ogniskowane za pomocą czaszy ogniskującej na anodzie w ognisku rzeczywistym.

Odbywa się tam zjawisko polegające na tym, że pola elektryczne jąder atomów anody działaj na wysokoenergetyczne elektrony co prowadzi do ich zahamowania. Podczas tego procesu 99% energii elektronów ulega rozproszeniu w postaci ciepła . Pozostała energia jest oddana w postaci promieniowania rentgenowskiego.

*Jeśli elektron ulegnie najpierw kilku zderzeniom niesprężystym to część energii traci podczas tych zderzeń.

*jeśli elektron straci całą energie podczas jednego gwałtownego hamowania to cała ta energia zostaje zamieniona na energie fotonu rentgenowskiego

Ognisko rzeczywiste - nazywamy miejsce na anodzie na które pada strumień elektronów.

Ognisko optyczne - nazywamy rzut ogniska rzeczywistego na płaszczyznę prostopadłą do przebiegu wiązki promieniowania elektromagnetycznego.

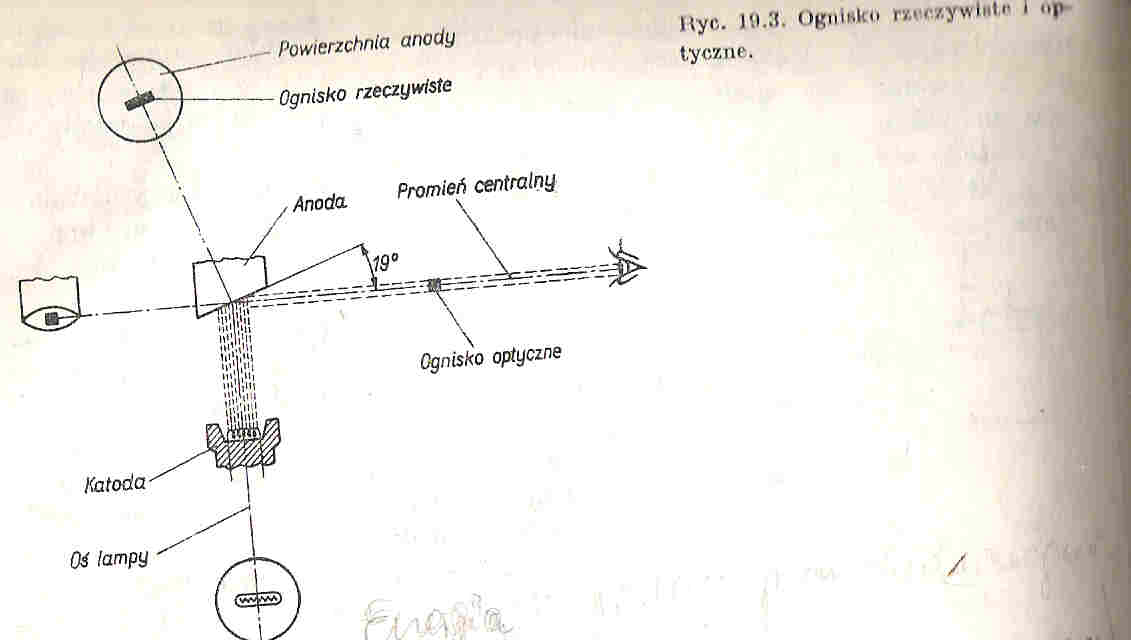
* rozmiary ogniska optycznego mają istotny wpływ na ostrość aparatu rentgenowskiego co jest ważne w lampach diagnostycznych

27. Powstawanie promieniowania rentgenowskiego, widmo ciągłe

Elektrony przyspieszone w silnym polu elektrycznym miedzy katoda, a anoda, przenikają w pobliże jader atomowych anody i pod działaniem pola elektrycznego atomu zostają zahamowane, uwalniając przy tym energie w postaci promieniowania elektromagnetycznego, o długości fali zależnej od wartości energii kinetycznej elektronu w okresie hamowania. Energia ta zależy od tego czy elektron straci od razu energie w procesie gwałtownego hamowania, czy najpierw dozna kilku zdarzeń niesprężystych z atomami anody, tracąc przy tym cześć energii, a po tym zostanie dopiero zahamowany. W tym pierwszym przypadku cala energia kinetyczna elektronów zostaje zamieniona na energie fotonu rentgenowskiego, dlatego promieniowanie emitowane przez lampę rentgenowska ma widmo ciągłe, czyli jest szerokim pasmem fal elektromagnetycznych o rożnych energiach i długościach fal. Rozkład energii widma jest na wykresie. Cechy charakterystyczne widma ciągłego:

1.istnienie ostrej granicy od strony fal krótkich. Związane z tym jest prawo Duane'a i Hanta,

U- napięcie anodowe

e- nabój elektronu

ν - częstość drgań krótkofalowej granicy widma

maksymalne ν otrzymamy gdy cala energie wypromieniowana zostanie w jednym fotonie. Max częstotliwość związana jest z minimalna w danym widmie długością fali, którą można otrzymać ze wzoru:

po podstawieniu h, c, i e otrzymuje się:

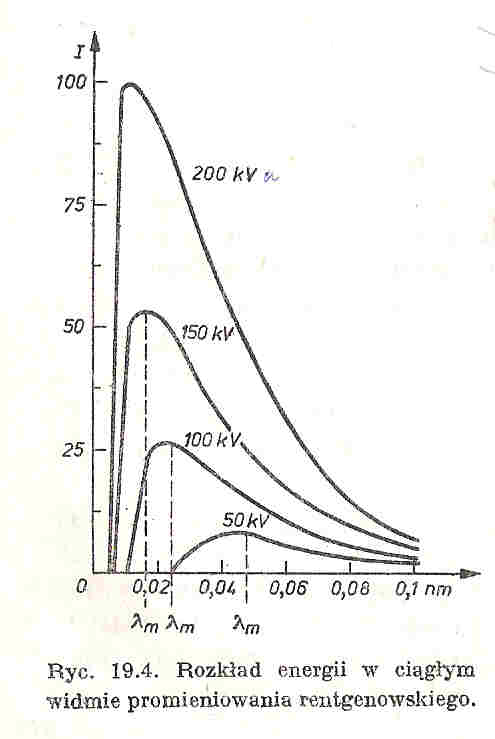
2. Gwałtowny wzrost natężenia promieniowania w miarę wzrostu napięcia anodowego, natężenie to jest proporcjonalne do kwadratu napięcia:

gdzie:

C - stała

Z - liczba atomowa materiału anody

i - natężenie prądu anodowego

U - Napięcie anodowe

28. Widmo charakterystyczne.

Na tle widma ciągłego występują wyraźne linie widmowe charakterystyczne dla pierwiastka, z jakiego jest zbudowana anoda. Powstaje wówczas, gdy energie elektronów przekroczy pewna konkretna wartość, która zależy od pierwiastka hamującego, wtedy spowoduje to przesuniecie sie elektronów orbitalnych atomów anody na wyższe poziomy energetyczne i powracając do stanu podstawowego emitują kwanty promieniowania rtg o energiach charakterystycznych dla danego pierwiastka. Są to głownie linie serii K i L, w przypadku cięższych pierwiastków M i N.

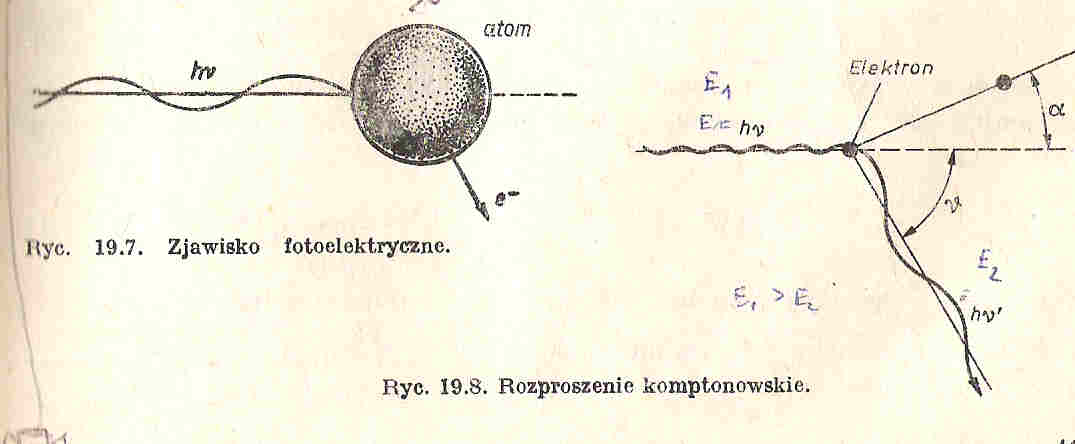
29. Zjawisko fotoelektryczne.

Zachodzi, gdy z atomu pod wpływem fali elektromagnetycznej zostaje wybity elektron, foton nadaje elektronowi energię kinetyczną 1/2mv².

Energia fotonu hv zostaje zużyta na wykonanie pracy W potrzebnej do przezwyciężenia energii wiązania elektronu (praca wyjścia) oraz na nadanie elektronowi energii kinetycznej.

hv= W + 1/2mv²

Atom pozbawiony elektronu staje się jonem dodatnim. Wybity elektron to fotoelektron.

30 . Rozproszenie Comptonowskie.

Wynik sprężystego zderzenia fotonu z elektronem. Po zderzeniu foton zostaje odrzucony, a foton rozproszony. Elektron uzyskuje pęd p=mv, a foton rozproszony ma mniejszą częstotliwość od fotonu padającego. Związany jest z tym przyrost długości fali.

Ponieważ¿ zderzenie fotonu z elektronem jest sprężyste, podlega zasadzie zachowania pędu:

oraz zasadzie zachowania energii:

-długość fali Comptona

31. Tworzenie par elektron-pozyton

Zjawisko to zachodzi w polu jądra atomowego i polega na wyzwoleniu przez foton dwóch elektronów o przeciwnych ładunkach elektrycznych-negatonu i pozytonu, przy jednoczesnym jego unicestwieniu(fotonu).Proces ten jest możliwy jedynie wtedy, gdy energia fotonu przekracza energie równoważna masie spoczynkowej dwóch elektronów, czyli musi być większa niż. 1,022MeV (E jednego elektronu=0,511MeV). Przekaz energii i pędu zachodzi za pośrednictwem jądra atomowego lub elektronu.

hν=2 m₀c²+Ek⁺ +Ek^-

Ek^- to energia kinetyczna elektronu Ek⁺ to energia kinetyczna pozytonu

Powstałe elektrony jonizują inne atomy kosztem swej energii kinetycznej. Pozyton po utracie energii łączy sie z negatonem, po czym oba elektrony ulęgają samounicestwieniu a na ich miejscu powstają 2 fotony.

32. Prawo osłabienia, współczynnik μ, warstwa połowiąca

Prawo osłabiania:

Mechanizmy oddziaływania promieniowania elektromagnetycznego z materia powodują, że wraz ze wnikaniem wiązki promieniowania w głąb środowiska, jej natężenie maleje w wyniku absorpcji i rozproszenia części fotonów. Spadek natężenia jest wyrażony prawem osłabiania, które głosi, że względne osłabianie natężenia promieniowania dI/I jest proporcjonalne do przyrostu grubości dx substancji pochłaniającej.

dI/I= - μdx

a po scałkowaniu:

I=I₀ e^-μx (I₀- natężenie wiązki padającej; I- wiązki po przejściu warstwy o grubości x)

gdzie: μ -współczynnik osłabiania, jego wartość zależy od masy właściwej absorbentu i długości fali promieniowania

Warstwa połowiąca:

Warstwa połowiąca d - grubość warstwy danego materiału powodująca

zmniejszenie o połowę natężenia przechodzącej przez nią wiązki

promieniowania. Odgrywa ona wazna role przy ocenie przenikliwosci promieniowania w radioterapii.

0.5I₀=I₀e^-μd

μd=lg2/lge=0.693

d=0.693/ μ

---