24.11.2009
TWIERDZENIE 2 Stolza
Niech ciąg ![]()
będzie dowolny a ciąg ![]()
niech będzie nieograniczony z góry i rosnący ![]()
Jeżeli ciąg ![]()
gdzie
![]()
jest zbieżny. To ciąg ![]()
też jest zbieżny do tej samej granicy.
TWIERDZENIE 3 o granicy średniej arytmetycznej
Jeżeli ciąg ![]()
jest zbieżny, to ciąg średnich arytmetycznych 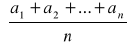
jest zbieżny do tej samej granicy.
Dowód
Niech ![]()
korzystamy z twierdzenia Stolza
![]()
![]()
Ciąg ![]()
jest rosnący i nieograniczony z góry. Ponadto mamy
![]()
Czyli
![]()
Twierdzenie odwrotne nie jest prawdziwe.
Podciągi
Niech będzie dany ciąg ![]()
oraz ciąg liczb naturalnych ![]()
przy czym ![]()
wtedy ciąg ![]()
nazywamy podciągiem ciągu ![]()
.
Podciąg ![]()
różny od ciągu ![]()
nazywamy podciągiem właściwym ciągu ![]()
Np. ciąg ![]()
, ![]()
są podciągami właściwymi ciągu ![]()
Jeżeli ciąg ![]()
, podciąg ciągu ![]()
jest zbieżny , to jego granicę nazywamy granicą częściową ciągu ![]()
.
TWIERDZENIE 4
Jeżeli ciąg ![]()
jest zbieżny do ![]()
lub rozbieżny ![]()
, to każdy jego podciąg jest zbieżny do ![]()
, lub rozbieżny do ![]()
.
Punkty skupienia ciągu.
Definicja
Ciąg ![]()
posiada punkt skupienia ![]()
jeżeli,
![]()
TWIERDZENIE 5 Bolzano-Weierstrussa
Każdy ograniczony ciąg liczb rzeczywistych posiada co najmniej jeden punkt skupienia.
Definicja
Największy punkt skupienia ciągu ograniczonego ![]()
nazywamy jego górną granicę
( lim superior)
Oznaczamy ![]()
lub ![]()
Najmniejszy punkt skupienia ciągu ograniczonego ![]()
nazywamy jego dolną granicę
( lim inferion)
Oznaczamy ![]()
lub ![]()
![]()
TWIERDZENIE 6
Jeżeli ciąg ![]()
jest ograniczony to równość ![]()
=![]()
zachodzi wtedy i tylko wtedy, gdy ciąg ![]()
jest zbieżny do wspólnej wartości obu granic ![]()
Definicja
Ciąg ![]()
nazywamy
rosnącym jeżeli
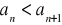
malejącym jeżeli
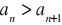
niemalejącym jeżeli
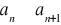
nierosnący
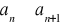
TWIERDZENIE 7
ciąg
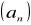
niemalejący, ograniczony z góry tzn.
![]()
jest zbieżny
ciąg
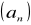
nierosnący, ograniczony z dołu tzn.
![]()
jest zbieżny
jeżeli ciąg
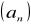
jest niemalejący i nieograniczony z góry to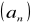
dąży do +∞jeżeli ciąg
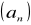
jest nierosnący i nieograniczony z dołu to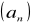
dąży do -∞
Definicja liczby e
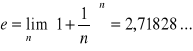
Ciąg 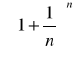
jest rosnący i ograniczony z góry, a więc zbieżny.
Liczba e jest liczbą niewymierną.
TWIERDZENIE 8
Niech ciąg![]()
, ![]()
≠0 , ![]()
, n=1,2… będzie dowolnym ciągiem dążącym do +∞,
a ![]()
, ![]()
≠0 , ![]()
, n=1,2… będzie dowolnym ciągiem dążącym do -∞ wtedy
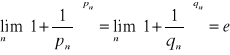
TWIERDZENIE 9
jeżeli p>0 to
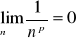
jeżeli p>0 to
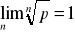
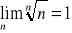
jeżeli p>0 , to
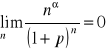
jeżeli |x|<1 to
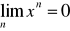
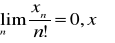
TWIERDZENIE 10 zasada zbieżności ciągu liczbowego
Ciąg ![]()
, ![]()
dla n=0,1,2… jest zbieżny wtedy i tylko wtedy, gdy jest spełniony warunek Couchy'ego
![]()
Szeregi o wyrazach rzeczywistych ![]()
Granice i ciągłość funkcji rzeczywistej jednej zmiennej
Granica funkcji rzeczywistej jednej zmiennej.
Definicja
Niech funkcja ![]()
![]()
będzie określona dla x takich, że 0<|x-x0|<a, a>0
Liczbę ![]()
nazywamy granicą funkcji ![]()
w ![]()
jeżeli
![]()
Piszemy wtedy
![]()
lub ![]()
przy ![]()
Interpretacja geometryczna funkcji ![]()
![]()
Dla ![]()
Własności funkcji posiadających granicę:
Funkcja
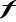
posiada w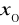
co najmniej jedną granicęNiech funkcja
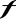
będzie określona dla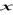
takich, że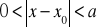
,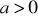
na to by funkcja ![]()
posiadała granicę ![]()
w ![]()
, potrzeba i wystarcza, by dla każdego ![]()
takiego, że ![]()
zbieżnego do ![]()
ciąg wartości funkcji ![]()
był zbieżny do ![]()
.
Jeżeli funkcja
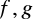
są określone w pewnym sąsiedztwie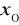
oraz posiada
granicę w ![]()
to, funkcja ![]()
![]()
posiada granicę w ![]()
oraz
![]()
![]()
Jeżeli ponadto ![]()
to i iloraz ![]()
posiada granicę w ![]()
oraz
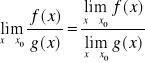
Jeżeli funkcja
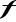
oraz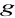
posiadają granicę w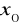
oraz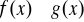
dla ![]()
,![]()
to ![]()
Twierdzenie o 3 funkcjach
Jeżeli funkcja ![]()
oraz ![]()
posiadają granicę ![]()
w ![]()
, oraz funkcja ![]()
jest określona i spełnia nierówność ![]()
w pewnym sąsiedztwie ![]()
, to ![]()
3
Wyszukiwarka