Model regresji liniowej dwóch zmiennych

Analiza regresji opiera się na modelu statystycznym. Przez model ten należy rozumieć „zbiór matematycznych wzorów i założeń, które opisują pewną sytuację zachodzącą w świecie rzeczywistym”. Chcemy oczywiście, by model wyjaśniał możliwie najlepiej procesy generujące wyniki obserwacji. Interesuje nas przy tym, by model ten był równocześnie oszczędny, to znaczy by „uchwycił” to, co w zachowaniach wyników obserwacji jest systematyczne, pozostawiając na uboczu czynniki przypadkowe, których skutki nie mogą być przewidziane. Czynniki te traktowane są jako błędy losowe.

Model statystyczny rozkłada więc w pewnym sensie wyniki obserwacji na składnik systematyczny i składnik losowy. Ten pierwszy reprezentowany jest przez określoną postać funkcji (czyli „wzór matematyczny”).

Składnik losowy ma natomiast swoje źródło w mechanizmach przypadkowych. Wyodrębnia się go ponieważ:

• badana zależność ma charakter stochastyczny,

• nie jest możliwe uwzględnienie i określenie wszystkich czynników wpływających na poziom badanego zjawiska,

• nie znamy dokładnej postaci analitycznej funkcji opisującej badaną zależność,

• pomiar zmiennych nie zawsze jest odpowiednio dokładny.

Model ten ma postać:

(1)

gdzie:

Y - zmienna objaśniana,

X - zmienna objaśniająca,

- parametry funkcji regresji,

U - składnik losowy, który w modelu jest jedynym źródłem losowości Y.

Prosty model regresji liniowej składa się ze składnika nielosowego (systematycznego) i błędu losowego.

Składnik systematyczny przedstawia średnie warunkowe wartości zmiennej Y przy danym X, co można zapisać następująco:

Jest to tzw. funkcja regresji pierwszego rodzaju.

Można również zdefiniować funkcję regresji pierwszego rodzaju w postaci:

Ogólnie biorąc prosty model regresji liniowej „funkcjonuje” przy następujących założeniach:

1. związek między zmiennymi X i Y jest liniowy,

2. wartości zmiennej objaśniającej X są ustalone, czyli nielosowe,

3. losowość wartości zmiennej Y pochodzi tylko i wyłącznie ze składnika losowego,

4. składnik losowy ma rozkład normalny (jakkolwiek nie jest to konieczne) o średniej 0 i stałej wariancji,

5. realizacje składnika losowego nie są ze sobą wzajemnie skorelowane.

Parametry modelu regresji muszą następnie zostać oszacowane na podstawie wyników obserwacji pochodzących z próby (zbiorowości). Wykorzystuje się w tym celu różne metody estymacji, z których najczęściej stosowana jest klasyczna metoda najmniejszych kwadratów (KMNK).

W rezultacie oszacowaną funkcją regresji Y względem X jest funkcja:

(2)

gdzie:

− oceny parametrów funkcji regresji typu (2)

U − reszty modelu regresji (2), które reprezentują realizacje składnika losowego modelu (1).

Funkcję regresji typu (2) określa się mianem funkcji regresji drugiego rodzaju.

Prezentacji tego modelu dokonamy przyjmując następujące założenia:

• badamy zależność między dwiema zmiennymi, przy czym zmienną objaśnianą oznaczamy przez Y, natomiast zmienną objaśniającą przez X.

Oczywiście, o tym którą ze zmiennych określamy jako objaśnianą, a którą jako objaśniającą decydują kryteria merytoryczne,

• pomiędzy wyróżnionymi zmiennymi występuje korelacyjny związek o kształcie liniowym, czyli:

Hipoteza ta w każdym indywidualnym przypadku musi być weryfikowana.

Algorytm analizy korelacji i regresji liniowej dwóch zmiennych przebiega w nastę-pujących etapach:

1. Specyfikacja zmiennych.

Na podstawie kryteriów merytorycznych określamy :

• zmienną objaśnianą - (Y),

• zmienną objaśniającą - (X).

2. Sporządzenie korelacyjnego diagramu rozrzutu.

Na jego podstawie wnioskujemy, czy związek korelacyjny występuje oraz czy można przyjąć, że jest to związek liniowy.

3. Określenie siły i kierunku związku korelacyjnego między badanymi zmiennymi.

Zakładamy przy tym, że:

• związek korelacyjny występuje,

• jest to związek o kształcie liniowym.

Wtedy jako miarę siły i kierunku zależności między badanymi zmiennymi stosujemy współczynnik korelacji liniowej Pearsona r .

Sposób liczenia tego współczynnika i jego interpretacja została już omówiona wcześniej. .

4. Estymacja parametrów liniowych funkcji regresji i ich prezentacja graficzna.

• Szacowanie parametrów funkcji regresji:

gdzie:

x_t - wartości zmiennej objaśniającej ( t = 1, 2, ..., N ),

a_y - wyraz wolny,

b_y - współczynnik regresji Y względem X.

Współczynnik regresji b_y ma swoją interpretację. Określa on mianowicie o ile przeciętnie biorąc zmieni się Y gdy zmienna X wzrośnie o jednostkę.

Korzystając z KMNK otrzymuje się, że:

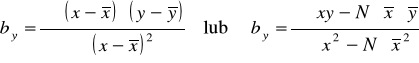
Można też obliczyć współczynnik regresji wykorzystując obliczony wcześniej współczynnik korelacji liniowej r :

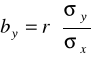
Natomiast wyraz wolny liczymy ze wzoru:

• Szacowanie parametrów funkcji regresji:

gdzie:

y_t - wartości zmiennej Y dla t = 1, 2, ..., N,

a_x - wyraz wolny,

b_x - współczynnik regresji X względem Y.

Współczynnik regresji b_x ma również swoją interpretację. Pokazuje mianowicie o ile przeciętnie biorąc zmieni się X jeśli Y wzrośnie o jednostkę.

Wykorzystując KMNK otrzymuje się, że:

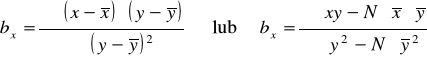
Lub podobnie jak w przypadku poprzedniej funkcji:

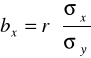
Natomiast wyraz wolny liczymy ze wzoru:

.

Warto zauważyć, że musi być spełniona relacja:

przy czym znak tych trzech współczynników musi być identyczny (wszystkie muszą być dodatnie lub ujemne).

Wykreślając oszacowane funkcje regresji na korelacyjnym diagramie rozrzutu znajdujemy dla każdej z nich dwa punkty, przez które musi ona przechodzić i następnie punkty te łączymy.

Współrzędne tych punktów są następujące:

• dla funkcji regresji Y względem X:

P₁ = (
),

P₂ = (
), gdzie
obliczamy podstawiając do funkcji regresji
za
wartość x₂ z przedziału określoności zmiennej X.

• dla funkcji regresji X względem Y:

P₁ = (
),

P₂ = (
), gdzie
obliczamy podstawiając do funkcji regresji
za
wartość y₂ z przedziału określoności zmiennej Y.

5. Ocena jakości oszacowanych funkcji regresji

Ocenie podlegają obie funkcje regresji. Ze względu na to, że proces ten przebiega podobnie uwagę swoją skierujemy na ocenę funkcji regresji Y wzglę-dem X.

Dokonując oceny jakości funkcji regresji chcemy uzyskać odpowiedź na pytanie: czy funkcja ta dobrze opisuje ilościową stronę zależności miedzy badanymi zmiennymi? Inaczej mówiąc, czy oszacowany model regresyjny jest dobrą kopią zjawiska wyjaśnianego, czy dobrze opisuje zachowanie się tego zjawiska.

Żeby odpowiedzieć na tak sformułowane pytanie oblicza się^:

1. odchylenie standardowe składnika losowego S_u:

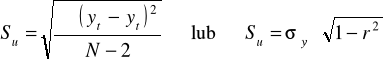
Miara ta określa o ile przeciętnie biorąc (+/-) wartości empiryczne zmiennej objaśnianej odchylają się od wartości teoretycznych tej zmiennej, obliczonych na podstawie oszacowanej funkcji regresji.

2. współczynnik zmienności losowej V_u^:

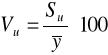
Parametr ten wskazuje jaki % średniego poziomu zmiennej objaśnianej stanowią wahania losowe, których miarą jest S_u. Parametr V_u jest więc miernikiem relatywnej wielkości błędu losowego. Błąd ten można umownie uznać za dopuszczalny, jeśli
,

3. Współczynnik determinacji R² :

Określa on jaki procent zmienności zmiennej objaśnianej został wyjaśniony przez oszacowaną funkcję regresji.

R² przyjmuje wartości liczbowe z przedziału < 0, 1 > (lub < 0 %, 100 % >), przy czym model regresji tym lepiej opisuje zachowanie się badanej zmiennej objaśnianej im R² jest bliższy jedności (bliższy 100 %). Zamiast współczynnika determinacji można użyć współczynnika zgodności
, który obliczamy korzystając z relacji:

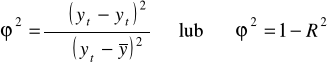
Współczynnik zgodności
określa jaka część zmienności badanej zmiennej objaśnianej nie została przez funkcję regresji wyjaśniona. Oczywiste jest więc, że korzystna sytuacja występuje wówczas, gdy
jest bliższy zera. Można umownie przyjąć, że model regresji jest dopuszczalny ze względu na kryterium
, jeśli ma on wartość mniejszą od 20 % (< 0,2).

4. Błędy średnie szacunku parametrów funkcji regresji:

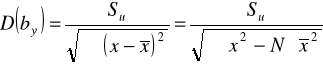
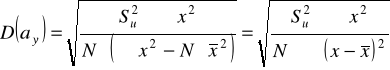
Błędy te wskazują o ile przeciętnie biorąc (+/-) odchylają się oceny parametrów modelu regresji od ich wartości prawdziwych, których przecież nie znamy. Jest przy tym pożądane, by błędy te były możliwie jak najmniejsze.

W związku z powyższym uznaje się w praktyce, że parametry funkcji regresji są precyzyjnie oszacowane, jeśli:

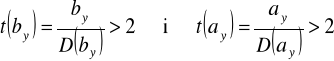
Przykład 1.

Kontynuujemy przykład, który przedstawiliśmy mówiąc o badaniu korelacji.

Dla 15 gospodarstw domowych 4-osobowych zebrano informacje o przychodach mie-sięcznych (w zł/1 osobę) i wysokości wydatków na utrzymanie mieszkania (w zł/1 osobę) w I półroczu 2007 r.:

X	594	450	395	520	648	695	825	800	687	650	430	874	808	609	765
Y	58	48	42	62	70	75	95	92	66	72	45	88	85	65	74

Y - wydatki na utrzymanie mieszkania w przeliczeniu na 1 osobę

X - przychody miesięczne w zł / 1osobę

Zamieszczony w poprzednim pliku diagram rozrzutu wskazuje na istnienie silnej, dodatniej korelacji między badanymi zmiennymi.

Potwierdził to wyliczony współczynnik korelacji:
.

Przypominamy wyliczone wcześniej parametry: średnie obu cech i ich odchylenia standardowe:

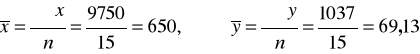
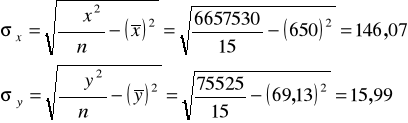
Prowadzimy analizę dalej, czyli szacujemy parametry funkcji regresji:

Liczymy współczynnik regresji wykorzystując obliczony wcześniej współczynnik

korelacji liniowej r :

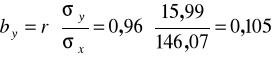
Natomiast wyraz wolny liczymy ze wzoru:

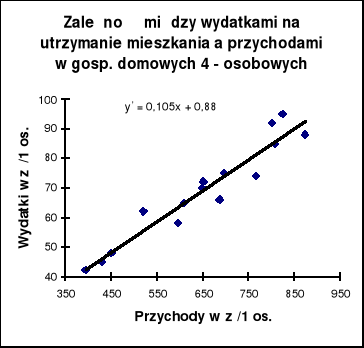
Funkcja regresji Y względem X ma więc postać:

Interpretujemy parametr
: wzrost dochodu o 1 zł na osobę w gospodarstwie domowym wiąże się ze wzrostem wydatków na utrzymanie mieszkania (na 1 osobę) przeciętnie o 0,105 zł.

Szacujemy parametry drugiej funkcji regresji:

.

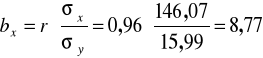
Funkcja ma więc postać:

Interpretujemy parametr
: Jeżeli wydatki na mieszkanie wzrosną o 1 zł to można przypuszczać, że dochody na jedną osobę wzrosły średnio o 8,77 zł.

Na wykresie prezentujemy tylko funkcję podstawową, czyli funkcję Y względem X: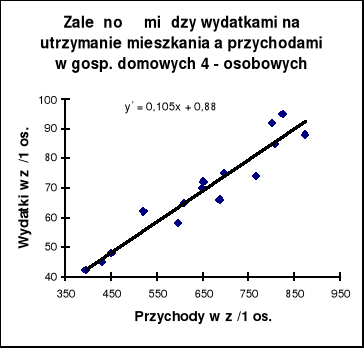

Dokonamy teraz oceny jakości oszacowanych funkcji regresji. Liczymy więc:

• odchylenie standardowe składnika losowego dla pierwszej funkcji:

Rzeczywiste wydatki na utrzymanie mieszkania różnią się od wydatków teoretycznych wyznaczonych w oparciu o funkcję regresji przeciętnie o +/- 4,48 zł.

• współczynnik zmienności losowej V_u:

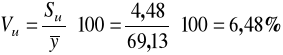
Wahania losowe stanowią 6,48 % średniego poziomu wydatków na utrzymanie mieszkania. Można więc przyjąć, że poziom błędu losowego jest dopuszczalny.

• współczynnik determinacji:

• współczynnik zgodności:

Parametry te informują nas, że zmiany w wydatkach na utrzymanie mieszkania związane są w 92,16 % ze zmianami przychodu na jedną osobę, natomiast w 7,84 % zależą od innych zmiennych, nie uwzględnionych w badaniu oraz od czynnika przypadkowego.

• błędy średnie szacunku parametrów funkcji regresji:

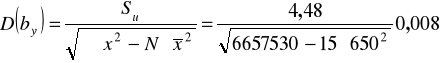
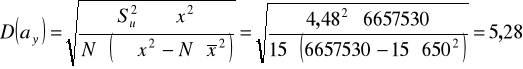
Uwzględniając obliczone błędy można funkcję zapisać następująco:

Porównując oszacowania parametrów z wielkością błędów zauważyć można, że wyraz wolny nie jest oszacowany precyzyjnie, natomiast precyzja szacunku współczynnika regresji jest wystarczająca.

Należy więc przyjąć, że przychód ma dużą moc wyjaśniania zmienności wydatków na utrzymanie mieszkania.

Przykład 2.

Badanie zależności między dostawami masła i skupem mleka w pewnej spółdzielni mleczarskiej w latach 1997 - 2006 dało następujące wyniki:

• średnie dostawy masła wynosiły 9 ton, a ich względna dyspersja 25 %,

• średni skup mleka wynosił w badanych latach 15,1 tys. litrów,

• odchylenie standardowe składnika resztowego liniowej funkcji regresji dostaw masła względem skupu mleka wyniosło 1,1 ton.

Ponadto wiadomo, że wzrost skupu mleka o 1 tys. litrów powoduje zwiększenie dostaw masła przeciętnie o 200 kg.

Mając powyższe informacje:

1. Określ siłę i kierunek badanej zależności.

2. Wyznacz rachunkowo obie funkcje regresji.

3. Oceń jakość funkcji regresji Y względem X.

4. Oszacuj wielkość dostaw masła przy planowanym skupie mleka równym 70 tys. litrów.

Rozwiązanie:

Ponieważ wielkość dostaw masła zależy od rozmiarów skupu mleka, wobec tego:

Y - dostawy masła (w tonach),

X - wielkość skupu mleka (tys. litrów).

Identyfikujemy informacje podane w treści zadania:

Wykorzystujemy współczynnik zmienności
i obliczamy odchylenie standardowe zmiennej Y: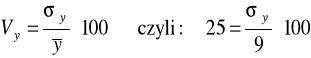

ad a) Liczymy współczynnik korelacji:

czyli:
z tego:

Odp. Między dostawami masła i skupem mleka występuje silna zależność liniowa o kierunku dodatnim.

ad b) Do pierwszej funkcji musimy wyznaczyć tylko wyraz wolny:

Funkcja ma więc postać:

Liczymy parametry drugiej funkcji regresji wykorzystując podany wcześniej wzór:

otrzymujemy

Liczymy wyraz wolny drugiej funkcji:

Druga funkcja ma postać:

Interpretujemy współczynnik regresji tej funkcji:

Na to, aby dostawy masła wzrosły o 1 tonę skup mleka musi wzrosnąć przeciętnie o 3,78 tys. litrów.

ad c) Obliczamy parametry struktury stochastycznej:

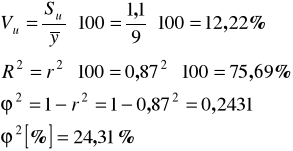
S_u =1,1 (podane w treści zadania) - rzeczywiste dostawy masła mogą różnić się od dostaw wyznaczonych za pomocą funkcji regresji przeciętnie o +/- 1,1 ton,

V_u =12,22% - odchylenia losowe stanowią przeciętnie biorąc 12,22 % średniego poziomu dostaw masła - jest to dopuszczalny poziom błędu,

R²,
- wielkość dostaw masła zależy w 75,69 % od wielkości skupu mleka, natomiast w 24,31 % od innych czynników, nie uwzględnionych w badaniu oraz od czynnika przypadkowego.

ad d) W odpowiedzi na to pytanie do funkcji regresji Y względem X w miejsce x_t podstawiamy planowany skup mleka, czyli 70 tys. litrów:

Jeżeli skup mleka wyniesie 70 tys. litrów to dostawy masła wyniosą 19,98 +/- 1,1 ton

1

8

---