Uogólniona metoda najmniejszych kwadratów

Założenia Gaussa-Markowa o składniku losowym:

4. Składnik losowy:

• ma rozkład o stałym odchyleniu standardowym:
  ,

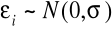
• nie występuje autokorelacja składnika losowego:
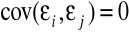
  dla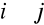
  ,

sprowadzają się do równania

,

tzn.: macierz wariancji i kowariancji składnika losowego jest macierzą diagonalną z wartościami równymi
na całej głównej przekątnej oraz zero poza nią.

W przypadku autokorelacji lub heteroskedastyczności modelu powyższy warunek nie zachodzi, lecz ma miejsce:

,

gdzie
jest macierzą symetryczną, dodatnio określoną.

Jeżeli znamy postać macierzy
lub jej oszacowanie
, to możemy dokonać estymacji parametrów liniowego modelu ekonometrycznego uogólnioną metodą najmniejszych kwadratów (UMNK). Wówczas wektor oszacowań parametrów modelu ma postać:

,

oszacowanie macierzy kowariancji ocen parametrów:

,

estymator wariancji składnika losowego:

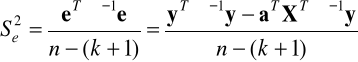
Model z heteroskedastycznym składnikiem losowym

W praktyce, gdy składnik losowy jest heteroskedastyczny, najczęściej mamy do czynienia z jednym z przypadków zmian w wartości wariancji składnika losowego:

• zmiany te następują w czasie (wariancja rośnie lub maleje z czasem),

• zmiany są proporcjonalne do wielkości pewnej zmiennej,

• obserwacje pochodzą z kilku podprób pochodzących z podpopulacji różniących się wielkością wariancji.

Zastosowanie klasycznej MNK do oszacowania parametrów modeli heteroskedastycznych powoduje, iż estymatory tychże parametrów nie są najbardziej efektywne. Postuluje się wówczas stosowanie innych metod estymacji (uogólnionej MNK, ważonej MNK) lub transformacji zmiennych. W wyniku stosowania np. uogólnionej MNK wartości ocen estymatorów parametrów z reguły nie ulegają zmianie, następuje jednak przeszacowanie błędów standardowych.

W modelu z heteroskedastycznym składnikiem losowym wariancja składnika losowego jest różna dla różnych obserwacji:
oraz

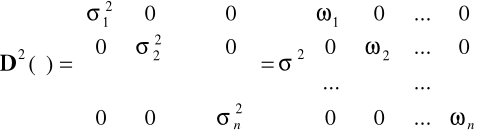
, zatem w tym przypadku

,
, zaś
oraz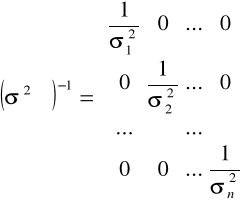
.

Nieznana macierz
, wariancja stała w podpróbach

W przypadku, gdy postać macierzy
jest znana, oceny parametrów uzyskuje się wprost z podanego wzoru, jednak najczęściej nie znamy postaci tej macierzy. Wówczas można dokonać pewnej jej estymacji. Nie dokonuje się jej jednak w przypadku ogólnym, ale tylko przy pewnych dodatkowych założeniach. Omówimy przypadek, gdy wariancja jest stała w podpróbach (dotyczących zwykle pewnych obiektów, w obrębie których dokonywane były obserwacje, np. regionów, przedsiębiorstw, gałęzi przemysłu itp.).

W tym przypadku macierz
ma postać:

,

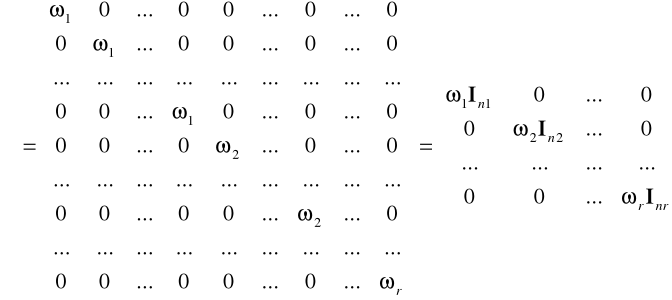
natomiast

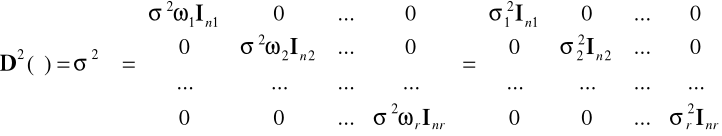
gdzie I_ni jest macierzą jednostkową rzędu n_i równemu liczebności i-tej podgrupy. Jeżeli wszystkie liczebności n_i są większe od liczby szacowanych parametrów k+1, to w każdej z podgrup należy oszacować osobno parametry modelu ekonometrycznego stosując KMNK, obliczyć wartości reszt dla tych modeli oraz wartości wariancji resztowych
, i=1, 2, ..., r w podgrupach. Wartości
są oszacowaniami wariancji składnika losowego
dla podgrup.

Ponieważ

zatem można wyznaczyć oceny parametrów modelu używając zamiast oszacowania macierzy
- oszacowania macierzy
.

Podobnie

,

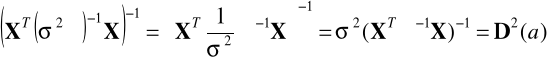
zatem oszacowanie macierzy wariancji i kowariancji ocen parametrów modelu można uzyskać w oparciu o macierz
zamiast macierzy
.

Przykład

Oszacujemy parametry oraz błędy dla danych dotyczących trzech zakładów o jednakowym profilu produkcji, w których badano zależność między stażem pracy pracowników mierzonym w latach (x), a wydajnością (określaną jako przeciętna liczba wykonanych operacji - y_i). W poprzednio omówionym przykładzie przy pomocy UMNK wyznaczono parametry modeli
dla trzech zakładów osobno i łącznie oraz wyznaczono dla nich wariancje resztowe.

x	y1	y2	y3		Zakład	a0	a1	S(a0)	S(a1)	R^2
0	20	22	20		I	24	10	4,90	2,00	0,89	40
1	40	36	38		II	24	10	3,58	1,46	0,94	5,33
2	40	44	44		III	24	10	1,79	0,73	0,98	21,33
3	60	56	58		Łącznie	24	10	1,75	0,72	0,94	15,39
4	60	62	60

W tym przypadku ocena macierzy wariancji i kowariancji składnika losowego ma postać

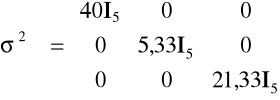
oraz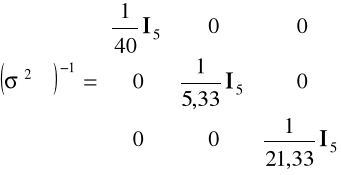
, otrzymamy zatem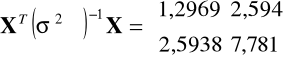
, a następnie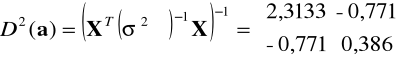
_i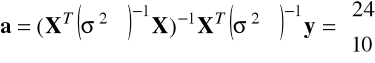
, zatem oszacowania parametrów modelu dla UMNK są takie same jak dla KMNK. Standardowe błędy szacunku parametrów modelu wynoszą

,
,

zatem są one mniejsze niż oszacowane dla KMNK.

Model z autokorelacją

Przyczyny autokorelacji

1. Błąd specyfikacji:

• pominięcie zmiennej objaśniającej,

• wadliwa struktura dynamiczna modelu (brak potrzebnych zmiennych opóźnionych),

• niepoprawna postać funkcyjna modelu,

2. Natura procesu:

1. bezwładność procesu,

2. psychologia i sposób podejmowania decyzji,

3. nieodpowiednio przetworzone zmienne.

W przypadku istnienia autokorelacji składnika losowego należy:

1. zmienić postać modelu,

2. zmienić sposób estymacji:

• zastosować uogólnioną metody najmniejszych kwadratów,

• dokonać transformacji zmiennych, np. zgodnie z metodą Cochrane'a-Orcutta (porównaj Gruszczyński)

Stosowanie testu Durbina-Watsona wymaga, by:

• w równaniu był obecny wyraz wolny,

• zakłócenia miały rozkład normalny,

• w równaniu nie występowała zmienna opóźniona jako zmienna objaśniająca (w tym przypadku stosujemy statystykę Durbina).

UMNK dla modeli z autokorelacją rzędu I

W przypadku modeli homoskedastycznych, stacjonarnych z autokorelacją macierz
ma postać:

,

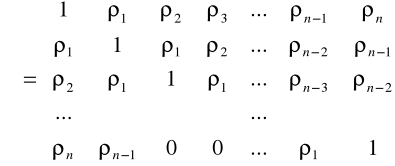
jeżeli zaś jest to model z autokorelacją rzędu pierwszego, tzn.

,

i bezpośrednia zależność występuje tylko między składnikami losowymi pochodzącymi z sąsiednich obserwacji, wówczas możemy zapisać:

,

(przy czym
są niezależnymi zmiennymi losowymi o jednakowych rozkładach ze średnią zero). Oczywiście także

, skąd

, a rozwijając dalej

i w końcu

,

a wyznaczając wartość wariancji składnika
otrzymamy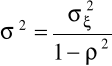
.

Wówczas kowariancje składnika losowego

zaś macierz wariancji i kowariancji składnika losowego ma postać

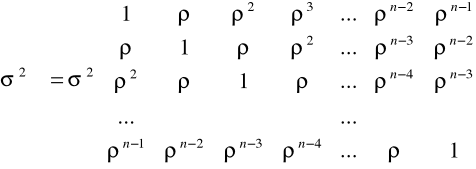
oraz

.

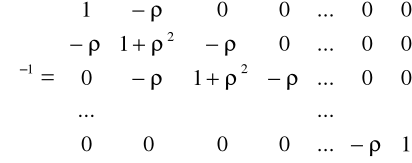
Ponieważ wartość współczynnika korelacji
nie jest zwykle znana, stosuje się jego oszacowanie

,

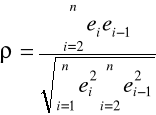
gdzie e_i są resztami modelu oszacowanego klasyczną metodą najmniejszych kwadratów.

Przykład:

Zastosujmy uogólnioną metodę najmniejszych kwadratów do przeszacowania parametrów i błędów modelu z przykładu dotyczącego banku „Grosik”. W tym przykładzie stosując KMNK na podstawie danych z 24 miesięcy oszacowano model sumy kredytów udzielanych gospodarstwom domowym z dwoma zmiennymi objaśniającymi: x₁ - przeciętne miesięczne wynagrodzenie netto, x₂ - kurs dolara w NBP:

. Dla reszt tego modelu oszacowano współczynnik korelacji liniowej równy
i uznano go za istotny za pomocą testu Durbina-Watsona.

W tym przypadku macierz
ma zatem postać:
i po odpowiednich obliczeniach otrzymujemy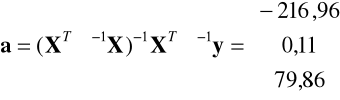
, zatem parametry modelu różnią się od oszacowanych KMNK.

Oszacowanie macierzy kowariancji ocen parametrów: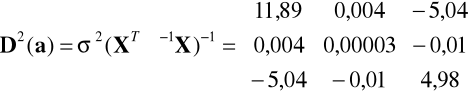
,

zatem S(a₀)=3,45, S(a₁)=0,006, S(a₂)=2,23.

Wartość estymatora wariancji składnika losowego wynosi:

.

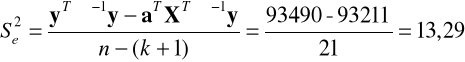
Dla tego modelu wartość współczynnika autokorelacji reszt rzędu I wynosi 0,39 (jest mniejszy niż poprzednio), zaś wartość statystyki testu autokorelacji Durbina-Watsona DW=0,86<d_l, to znaczy, że oszacowany model nie jest jednak wolny od autokorelacji. Należy prawdopodobnie zmienić postać modelu lub zastosowanych w nim zmiennych.

Transformacja zmiennych w przypadku autokorelacji rzędu I

Dla modeli z autokorelacją składnika losowego stosuje się często transformację zmiennych polegającą na tym, że zamiast oryginalnych zmiennych x_i, y stosuje się zmienne:

,

,

,

gdzie
jest oszacowaniem współczynnika autokorelacji składnika losowego dla modelu oszacowanego przy pomocy KMNK.

Dla powyższych zmiennych szacuje się parametry modelu klasyczną MNK.

Przykład:

Dla danych z poprzedniego przykładu zastosujemy transformację zmiennych, otrzymując:

,
,
. Przekształcone dane będą miały postać:

Lp.
1
2	338,42	1,24	32,83	32,82	0,01
3	366,29	1,26	33,00	36,83	-3,83
4	374,08	1,29	35,68	40,34	-4,66
5	374,08	1,31	38,09	42,23	-4,13
6	354,40	1,33	40,06	41,31	-1,25
7	395,52	1,31	42,93	43,92	-0,99
8	360,77	1,33	45,04	41,91	3,13
9	376,21	1,37	48,35	46,61	1,74
10	416,55	1,38	52,15	51,87	0,28
11	434,78	1,36	54,83	52,13	2,70
12	479,41	1,40	61,32	59,87	1,46
13	366,46	1,45	59,20	52,09	7,11
14	411,29	1,51	61,20	61,71	-0,51
15	448,02	1,51	64,59	65,36	-0,77
16	454,04	1,53	68,20	67,09	1,11
17	433,63	1,56	70,34	67,28	3,05
18	493,10	1,60	75,84	76,87	-1,03
19	477,57	1,71	77,05	84,20	-7,15
20	432,04	1,73	79,30	80,47	-1,17
21	472,42	1,65	81,76	78,63	3,13
22	500,36	1,63	85,92	80,37	5,55
23	516,83	1,74	86,60	90,35	-3,74
24	574,99	1,70	93,43	93,47	-0,04

Należy zauważyć, że transformacja zmiennych powoduje utratę jednej obserwacji. Dla powyższych danych oszacowano model
. Dla tego modelu wyznaczono wartości teoretyczne i reszty (w tabeli). Na podstawie reszt oszacowano wartość współczynnika autokorelacji składnika losowego wynoszącą 0,27 oraz wyznaczono wartość DW=1,47. Dla poziomu istotności 0,05 i n=23, k=2 mamy d_l=1,17 oraz d_u=1,54, zatem wartość statystyki DW wskazuje na obszar niekonkluzywności (w przypadku poziomu istotności 0,1 d_u=1,29, zatem dla tego poziomu uznalibyśmy brak istotnej autokorelacji rzędu I składnika losowego).

Metoda pierwszych różnic zmiennych w przypadku autokorelacji rzędu I

W przypadku, gdy wartość współczynnika autokorelacji reszt jest bliska 1, można przyjąć r=1 i wówczas w opisanej procedurze transformacji zastępuje się oryginalne wartości zmiennych ich przyrostami. Następnie szacuje się parametry dla modelu opartego na przyrostach. Upraszcza to obliczenia oraz interpretację otrzymanych wyników, jednak zdarza się, że otrzymany model jest mniej efektywny.

---