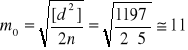Różnice spostrzeżeń
Zwykle każdy pomiar wykonujemy (dla kontroli) dwukrotnie. W ten sposób otrzymane pary spostrzeżeń stanowią ogromny materiał doświadczalny, który pozwala wyciągnąć wnioski odnośnie dokładności danego typu pomiarów. Na teorii różnic par wyników pomiarów oparta jest duża ilość prac badających błędy średnie pomiarów.
Oznaczmy wagi obu spostrzeżeń przez ![]()
i ![]()
, a wyniki pomiarów przez ![]()
i ![]()
. Różnicę obu pomiarów oznaczmy przez d. Mamy, więc
![]()
![]()
![]()
Średnia arytmetyczna ważona ![]()
i ![]()
, to
![]()
.
Stąd poprawki
![]()
, ![]()
.
Z powyższych zależności wynika, że
![]()
,
co oznacza, że różnica d jest rozdzielona na oba spostrzeżenia odwrotnie proporcjonalnie do ich wag.
Błąd średni jednostkowy jest równy
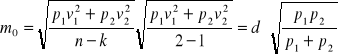
,
a błędowi średniemu średniej arytmetycznej ważonej odpowiada następująca zależność
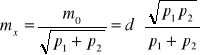
.
Jeżeli spostrzeżenia są jednakowo dokładne wówczas:
![]()
,
![]()
, ![]()
,
![]()
,
![]()
.
Wzory te pozwalają na podstawie wyników podwójnych pomiarów tej samej wielkości wnioskować o błędach średnich zarówno samych pomiarów, jak średniej arytmetycznej, która została z nich obliczona. Uwaga! Obliczenia te trzeba oprzeć o większą liczbę spostrzeżeń ponieważ wnioski oparte tylko na dwóch pomiarach nie są pewne.
Przede wszystkim zauważmy, że różnica spostrzeżeń ma charakter błędu prawdziwego. Jeśli rozpatrujemy funkcję
![]()
(f1)
to dla ![]()
funkcja f jest równa zeru. Znamy, więc jej wartość prawdziwą, która jest równa właśnie zeru. Natomiast z pomiarów ![]()
otrzymujemy jej wartość w postaci
![]()
A więc błąd prawdziwy różnicy wynosi
![]()
.
Do równania (f1) możemy zastosować prawo przenoszenia się błędów średnich otrzymując
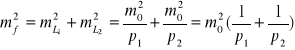
.
dla ![]()
otrzymamy
![]()
![]()
![]()
co można napisać również jako
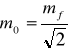
.
Z powyższych rozważań można wysnuć następujące wnioski:
Jeżeli mamy szereg różnic z pomiarów o jednakowej dokładności, przy czym każda różnica odnosi się do dwóch pomiarów tej samej wielkości prawdziwej wówczas każdą różnicę możemy uważać za błąd prawdziwy wielkości o prawdziwej wielkości równej zeru. Z tych różnic możemy, więc obliczyć średnią różnicę ![]()
, która będzie w myśl definicji błędem średnim funkcji ![]()
. A więc
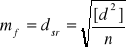
.
gdzie n jest ilością różnic. Obecnie korzystając z wzoru 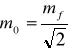
możemy obliczyć błąd średni pojedynczego pomiaru
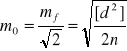
.
Gdyby nas interesował błąd średni średniej arytmetycznej dwóch pomiarów, wówczas
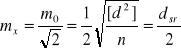
.
Jeżeli każda para składa się z pomiarów o tej samej dokładności, ale różne pary mają dokładność niejednakową, wówczas w celu obliczenia błędu średniego różnicy o wadze równej jedności można zastosować wzór ![]()
,w którym zamiast błędów prawdziwych ![]()
, ![]()
,…,![]()
wstawiajmy różnice ![]()
, ![]()
,…,![]()
(traktowane jako błędy prawdziwe). Otrzymamy, więc
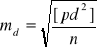
,
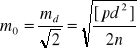
. (m1)
Zależność ta podaje błąd średni pojedynczego pomiaru o wadze równej jedności, za pomocą n różnic pomiarów, przy czym każda para pomiarów ma wagę ![]()
, ![]()
,…,![]()
. Stąd dla średniej arytmetycznej dwóch pomiarów o wadze równej jedności błąd średni określony jest następującym wzorem
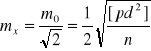
(m2)
Wzory m1 i m2 mają szerokie zastosowanie w znajdowaniu błędu średniego jednokilometrowego odcinka (1 km) niwelacji lub pomiaru długości. Ponieważ w tych dwóch wypadkach błędy rosną proporcjonalnie do pierwiastka z długości s, więc wagi są odwrotnie proporcjonalne do s. Przyjmując, dlatego
![]()
otrzymamy wzory (m1) i (m2) w postaci
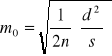
, 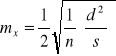
.
Dotychczas przyjmowaliśmy, że źródłem niedokładności są wyłącznie błędy przypadkowe. Jeżeli zorientujemy się, że w pomiarach są obecne błędy systematyczne, wówczas błąd ten możemy oszacować z zależności
![]()
.
Różnice d poprawiamy odejmując od nich wartość ![]()
. Poprawione w ten sposób różnice tracą charakter błędów prawdziwych, dlatego aby wyznaczyć odpowiadający im błąd średni należy zastosować wzór odnoszący się do poprawek tj. błąd średni różnicy dwóch pomiarów ![]()
obliczyć następująco
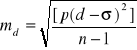
, 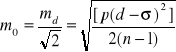
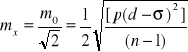
.
Przykład. (różnice o jednakowej dokładności). Przeróbmy obecnie przykład na stosowanie teorii różnic do obliczania błędu średniego pomiaru. Rozważania nasze ze względu na oszczędność miejsca zacieśnimy do niewielkiej ilości par spostrzeżeń. W zastosowaniach tej teorii operujemy zazwyczaj wielką ilością par spostrzeżeń. Mamy kąty pomierzone na pięciu stanowiskach dwukrotnie, z jednakową dokładnością. Na tej podstawie mamy obliczyć błąd średni pojedynczego pomiaru kąta. Dane i obliczenia zestawiono w poniższej tabeli.
Nr |
Pomiar I |
Pomiar II |
Średnia |
d |
d2 |
Obliczenia |
1 |
27°35'12" |
27°35'20" |
27°35'16" |
+8 |
64 |
|
2 |
112°2410" |
112°2402" |
112°2406" |
-8 |
64 |
|
3 |
148°17'50" |
148°17'32" |
148°17'41" |
-18 |
324 |
|
4 |
216°05'05" |
216°04'52" |
'216°04'58" |
-13 |
169 |
|
5 |
165°48'52" |
165°49'16" |
165°49'04" |
24 |
576 |
|
|
|
|
|
[d]=-7 |
1197 |
|
A więc gdybyśmy wykonywali w tych samych warunkach na każdym stanowisku pojedynczy pomiar kąta, wówczas na podstawie powyższych pięciu wyników moglibyśmy się spodziewać błędu średniego 11" na stanowisko. Gdybyśmy jednak wykonywali dwukrotny pomiar kąta na stanowisko, wówczas błąd średniej arytmetycznej tych dwu pomiarów oceniamy na 7,7".
Przykład. (Na różnice o niejednakowej dokładności)
W wyniku przeprowadzonych pomiarów otrzymano dziesięć ciągów niwelacyjnych o niejednakowej długości, niwelację prowadzono dwukrotnie w przeciwnych kierunkach. Różnice d otrzymane z każdej pary uzyskanych w ten sposób spostrzeżeń zestawiono w poniższej tablicy. Należy określić błąd średni różnicy wysokości dwóch sąsiednich pikiet (na jednym stanowisku) i błąd średni niwelacji na długości jednego kilometra.
Wagi ![]()
dla i - tego ciągu obliczono według wzoru
![]()
gdzie ![]()
oznacza ilość stanowisk w i-tym ciągu. A więc wagę p = 1 przyjęto dla 1000 stanowisk. Ponieważ jedno stanowisko przypada przeciętnie na 100 metrów niwelacji, więc dla 1 km niwelacji przyjęto 10 stanowisk.
Nr, i |
|
|
|
|
|
Obliczenia |
1 |
- 4 |
20 |
50 |
16 |
800 |
|
2 |
+ 3 |
19 |
53 |
9 |
477 |
|
3 |
- 2 |
18 |
56 |
4 |
224 |
|
4 |
+ 8 |
25 |
40 |
64 |
2560 |
|
5 |
+ 1 |
10 |
100 |
1 |
100 |
|
6 |
- 5 |
16 |
62 |
25 |
1550 |
|
7 |
+ 1 |
12 |
83 |
1 |
83 |
|
9 |
- 2 |
14 |
71 |
4 |
284 |
|
9 |
+4 |
17 |
59 |
16 |
944 |
|
10 |
- 4 |
21 |
48 |
16 |
768 |
|
[pdd]=7790 |
|
|||||
W tabeli obliczono błąd ![]()
dla 1000 stanowisk, błąd ![]()
dla 1 stanowiska oraz błąd ![]()
dla 1 km niwelacji. Z powyższych danych wynika, że błąd średni popełniony na jednym stanowisku wynosi 0,6 mm, błędowi średniemu 1 km niwelacji odpowiada około 2 mm. W przypadku niwelacji wykonanej dwukrotnie, wynik ten należy podzielić przez ![]()
. A więc
![]()
.
W przykładzie tym nie uwzględniono błędu systematycznego, ponieważ zarówno liczba znaków różnic dodatnich równa się liczbie znaków różnic ujemnych jak również suma tych różnic wynosi zero. Taka idealna zgodność nie jest zresztą konieczna, by nie uwzględniać wpływu błędów systematycznych.
Przykład. (różnice o niejednakowej dokładności z błędem systematyczny m).
Wykonano dziesięć par ciągów niwelacyjnych. Różnice dla poszczególnych par wraz z ilością stanowisk dla każdego ciągu przedstawiono w poniższej tabeli. W różnicach zauważono dość znaczną przewagę błędów dodatnich nad ujemnymi, co wskazuje na istnienie błędu systematycznego. Po wyeliminowaniu wpływu tego błędu mamy obliczyć błąd średni przypadkowy niwelacji na długości 1 km.
Błąd systematyczny na jedno stanowisko to:
![]()
Przyjmując, że błąd systematyczny jest stały dla każdego stanowiska można obliczyć wielkość błędu systematycznego dla każdego ciągu posługując się następującą zależnością
![]()
.
Przyjmując za pomiar o wadze równej jedności ciąg niwelacyjny składający się z 1000 stanowisk otrzymamy błąd średni typowego spostrzeżenia (dla 1000 stanowisk)
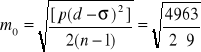
= 16,6 mm
Stąd błąd pojedynczego stanowiska to
![]()
a błąd średni na długości 1 km niwelacji tj. przypadający na 10 stanowisk:
![]()
1,66 mm.
i |
|
|
|
|
|
|
|
1 |
+ 3 |
13 |
77 |
+ 3 |
0 |
0 |
0 |
2 |
+ 4 |
15 |
66 |
+ 4 |
0 |
0 |
0 |
3 |
+ 6 |
14 |
71 |
+ 4 |
+ 2 |
4 |
284 |
4 |
- 2 |
8 |
125 |
+ 2 |
- 4 |
16 |
2000 |
5 |
+ 10 |
24 |
42 |
+ 7 |
+ 3 |
9 |
378 |
6 |
+ 7 |
20 |
50 |
+ 5 |
+ 2 |
4 |
200 |
7 |
+ 4 |
15 |
66 |
+ 4 |
0 |
0 |
0 |
8 |
- 1 |
13 |
77 |
+ 4 |
- 5 |
25 |
1925 |
9 |
+ 5 |
17 |
59 |
+ 5 |
0 |
0 |
0 |
10 |
+ 8 |
23 |
44 |
+ 6 |
+ 2 |
4 |
176 |
|
+44 |
162 |
|
|
0 |
|
4963 |
1
Wyszukiwarka