Na dzisiejszych zajęciach przejdziemy do algorytmu usuwania elementu z uporządkowanej listy jednokierunkowej. Głównym celem takiej operacji jest usunięcie elementu z listy, natomiast danymi wejściowymi będzie wskaźnik na pierwszy element listy - startPtr, oraz opis usuwanego elementu jak na przykład wartość danej elementarnej. Pełny algorytm tej operacji przedstawia się tak:

1. Jeżeli dane są zgodne z danymi pierwszego elementu listy - usuń pierwszy element listy.

2. Znajdź element do usunięcia w liście.

3. Jeżeli nie znaleziono elementu, generuj komunikat.

4. Usuń znaleziony element.

Oto jak wygląda pełna implementacja tego algorytmu w języku c++:

A oto, jak ten algorytm prezentuje się w postaci graficznej:

Kolejna rzecz, którą będziemy omawiać na dzisiejszych zajęciach, to zastosowanie liniowych struktur danych. Definicja listy stanowi podstawę do zdefiniowania struktury liniowej. Wszystkie przypadki struktur liniowych można zdefiniować bazując na ich odpowiednich reprezentacjach listowych. I teraz jakie mamy te linowe struktury danych. Będą to kolejki, stosy, napisy, tablice sekwencyjne, tablice rzadkie i tablice rozproszone. Zacznijmy od kolejek. Kolejka jest trukturą danych wykorzystywaną najczęsciej jako bufor przechowujący dane określonych typów. Mamy cztery takie podstawowe rodzaje kolejek:

1. FIFO, gdzie pierwszy element wchodzący staje się pierwszym elementem wychodzącym.

2. Round robin - Jest to kolejka cykliczna z dyscypliną czasu obsługi komunikatu przechowywanego w kolejce. Wykorzystywana jest głównie w sieciach komputerowych, oraz w systemach operacyjnych.

3. LIFO, gdzie ostatni wchodzący staje się pierwszym wychodzącym (stos).

4. Kolejki priorytetowe, gdzie dodatkowo w starym mechanizmie kolejki uwzględnia się wartości priorytetów przechowywanych danych.

Zobaczmy na rysunkach, jak wygląda dyscyplina dwóch podstawowych kolejek - FIFO i LIFO:

Po wstępnym omówieniu kolejek popatrzmy, jakie są realizacje struktur liniowych. Mamy trzy i są one następujące:

1. Realizacje sekwencyjne - Stosujemy, gdy z góry znamy maksymalny rozmiar przetwarzanej struktury liniowej i z góry chcemy zarezerwować dla niej określony zasób (pamięć operacyjna, pamięć zewnętrzna). W czasie wytwarzania programów komputerowych bazujemy wtedy na zmiennych statycznych.

2. Realizacje dynamiczne (łącznikowe) - Stosujemy, gdy rozmiar struktury nie jest z góry z znany i w czasie jej przetwarzania może istnieć konieczność dodawania do niej nowych elementów, lub ich usuwania. Bazujemy wtedy na zmiennych dynamicznych (wskaźnikowych).

3. Realizacje dynamiczno sekwencyjne - Jest to połączenie obydwu powyższych metod i stosujemy wtedy, gdy konieczny jest odpowiedni balans pomiędzy zmiennymi statycznymi i dynamicznymi.

Przejdżmy teraz do wnikliwej analizy kolejki FIFO, LIFO i priorytetowej. Zacznijmy jednak od tej drugiej. Spójrzmy wpierw, jak wygląda implementacja stosu kolejki LIFO:

W praktyce wykorzystuje się tu wiele różnych implementacji stosu jak przykładowo realizacja tablicowa, czy realizacja dynamiczna (wskaźnikowa) z użyciem list. Wyróżniamy sześć podstawowych i typowych operacji na takim stosie. Są to:

1. clear() - czyszczenie stosu.

2. isEmpty() - sprawdzenie, czy stos jest pusty.

3. isFull() - Sprawdzenie, czy stos jest pełny.

4. push(wartosc) - Włożenie na stos wartości wartosc.

5. pop() - Zdjęcie ze stosu ostatniego elementu

6. top() - Odczytanie bez zdejmowania ostatniego elementu.

Popatrzmy na tablicową realizację stosu dla tej kolejki:

No i teraz czas na listową realizację stosu kolejki LIFO. Nim zobaczymy implementacje warto znać 5 reguł:

1. Najwygodniej stos jest implementować za pomocą jednkoierunkowej listy niecyklicznej.

2. Korzeń listy zawsze wskazuje na element szczytowy.

3. Włożenie nowego elementu na stos realizowane jest poprzez dodanie go na początek listy.

4. Zdjęcie elementu ze stosu polega na usunięciu pierwszego elementu listy.

5. Stos nie ma ograniczenia a liczbę elementów.

No i teraz implementacja listowej realizacji stosu tej kolejki:

I teraz przejdźmy do kolejki FIFO. Na sam początek implementacja:

W praktyce wykorzystuje się wiele różnych implementacji tej kolejki jak przykładowo realizacja tablicowa, czy realizacja dynamiczna (wskaźnikowa) z użyciem list. Wyróżniamy następujące typowe operacje na kolejce:

1. clear() - czyszczenie stosu.

2. isEmpty() - sprawdzenie, czy stos jest pusty.

3. isFull() - Sprawdzenie, czy stos jest pełny.

4. enqueue(wart) - Wstawienie do kolejki wartości wart.

5. dequeue() - Usunięcie z kolejki pierwszego elementu.

6. first() - Odczytanie (bez usuwania) pierwszego elementu.

Należy podkreślić iż kolejka FIFO jest trudniejsza w implementacji, niż stos. Jeśli chodzi o implementację tablicową, to w niej często stosuje się takzwaną tablicę cykliczną. Wymagane są przy takiej implementacji dwa podstawowe wskaźniki - head (wskazuje na początek kolejki) i tail (wskazuje na koniec kolejki).

Wstawienie elementu do kolejki zwiększa tail o 1, zaś usunięcie elementu z kolejki zwiększa head o 1. W tablicy cyklicznej natomiast może być problem z określeniem, czy kolejka jest pusta, czy pełna.

Wówczas możliwe są dwa rozwiązania. Możliwe jest wprowadzenie nowej zmiennej, która przechowuje liczbę elementów w kolejce, oraz uzycie tablicy o jedną pozycję dłuższej niż liczba elementów kolejki. Kolejka jest pusta, gdy spełniony jest nastepujący warunek:

(tail+1)%RozmiarKolejki==head. Z kolei kolejka jest pełna, gdy jest spełniony warunek:

(tail+2)%RozmiarKolejki==head

I teraz rzućmy okiem na tablicową realizację kolejki FIFO:

I a koniec zostaje nam kolejka priorytetowa. Implementacja kolejek priorytetowych jest trudniejsza niż implementacja zwykłych kolejek (o kolejności pobierania elementów z kolejki decyduje ich priorytet). Zasad ustalania priorytetów z kolei może być wiele. Oto cztery przykładowe możliwości implementacji kolejki priorytetowej:

1. Za pomocą listy uporządkowanejwedług kluczy (złozoność wstawiania elementu do kolejki wynosi O(1), a pobieranie ma złożoność O(n)).

2. Za pomocą listy uporządkowanej według priorytetów (złozoność wstawiania elementu do kolejki wynosi O(n), a pobieranie ma złożoność O(1)).

3. Za pomocą dwóch list: Krótkiej uporządkowanej według priorytetów i listy nieuporządkowanej pozostałych elementów. Liczba elementów na liście krótkiej zależy od tak zwanego priorytetu progowego (złozoność wstawiania elementu do kolejki wynosi O(
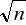
   ), a pobieranie ma złożoność O(1)).

4. Za pomocą kopca (złożoność operacji wstawiania / pobierania elementu do / z kolejki wynosi O(lg n)).

Kopiec może być tu podstawą bardzo efektywnej implementacji kolejki priorytetowej. Aby wstawić element do kolejki dodaje się go na koniec jako ostatni liść (należy wówczas najczęściej odtworzyć własnośc kopca). Pobieranie elementu z kolejki z kolei polega na pobraniu wartości z korzenia. Na jego miejsce przesuwany jest ostatni liść (należy wtedy odtworzyć własnośc kopca). Implementacja kolejki priorytetowej za pomocą kopca będize przedmiotem kolejnego wykładów.

---